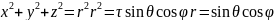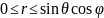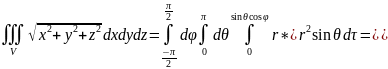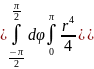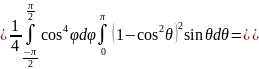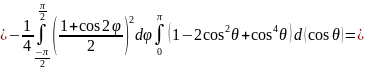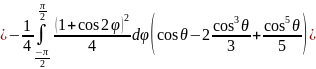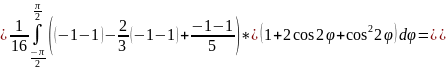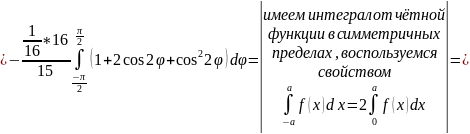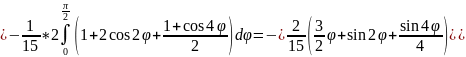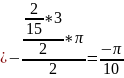- •Кратные интегралы Двойные интегралы
- •§1. Задача об оъёме цилиндрического бруса.
- •§2. Понятие двойного интеграла.
- •§3. Свойства двойного интеграла.
- •§4. Вычисление двойного интеграла.
- •Свойства двукратного интеграла
- •Оценка двукратного интеграла
- •Теорема о среднем.
- •§5 Замена переменных в двойном интеграле.
- •6. Вычисление площадей и объёмов с площадью двойных интегралов.
- •§7 Тройной интеграл, масса неоднородного тела.
- •§8 Вычисление тройного интеграла.
- •Теорема об оценке трёхкратного интеграла.
- •Теорема о среднем.
- •§9 Вычисление объёма тел с помощью тройного интеграла.
- •§10 Замена переменных в тройном интеграле.
- •Общая замена переменных в тройном интеграле.
- •Т ройной интеграл в цилиндрических координатах.
- •Тройной интеграл в сферических координатах.
Тройной интеграл в сферических координатах.
П оложение
т. Р в сферических координатах определяется
3мя
числами
оложение
т. Р в сферических координатах определяется
3мя
числами
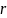 ,φ,θ,
где
,φ,θ,
где
- расстояние т. Р от начала координат – радиус-вектор т.
θ – угол между радиус-вектором и осью oz.
φ – угол между проекцией радиус-вектора на плоскость xoy и осью ox.
Для любой точки пространства имеем:
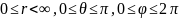
Связь между декартовыми и сферичеcкими координатами:
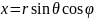
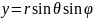
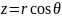
Якобиан перехода будет равен:

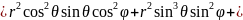
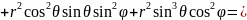
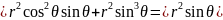
Тогда
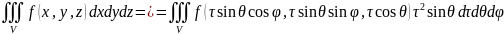
Пример 1:
Вычислить
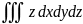 ,
,
где
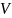 – область, ограниченная поверхностями
– область, ограниченная поверхностями
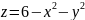 и
и
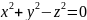
параболоид
вращения, ось вращения
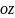 .
.
конус, ось симметрии .
Построим эту область.
Л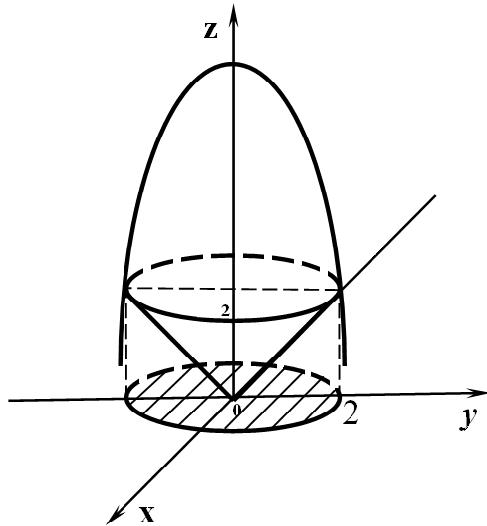 иния
пересечения этих поверхностей
иния
пересечения этих поверхностей
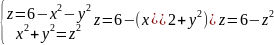
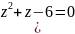
окружность
П роще
вычислить этот интеграл в цилиндрических
координатах.
роще
вычислить этот интеграл в цилиндрических
координатах.


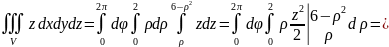
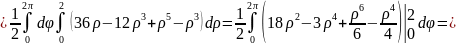
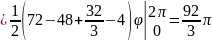
Пример 2:
Вычислить
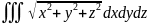 ,
,
где
– область, ограниченная сферой
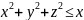 .
.
Приведём уравнение сферы к каноническому виду:
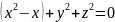
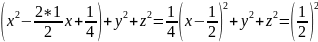
ц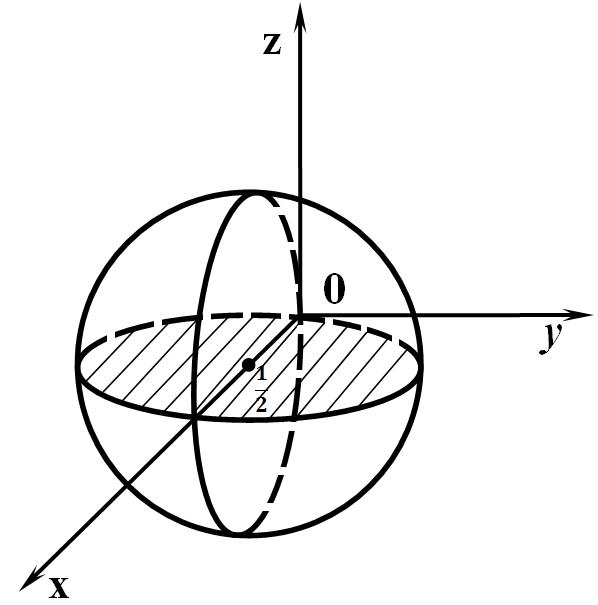
 ентр
сферы в т.
ентр
сферы в т.

Удобнее этот интеграл вычислять в сферических координатах.
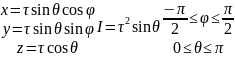
Уравнение сферы в сферических координатах: