§8 Вычисление тройного интеграла.

Пусть дана трёхмерная обл. V, ограниченная замкнутой поверхностью S. Она обладает следующими свойствами:

1. Всякая прямая, параллельная оси oz, проходящая через внутреннюю т. обл. V, пересекает поверхность S в двух точках.

2. Вся область V проектируется на пл. oxy в правильную обл. D

Обл. V, обладающую указанными свойствами, называют правильной трёхмерной областью.

Т акую область можно задать следующим образом:

причём

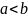
Выражение вида

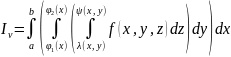
называют трёхкратным интегралом.

Вычисление начинают с внутреннего интеграла

а далее как в двукратном интеграле.

Трёхкратный интеграл имеет те же свойства что и двухкратный интеграл

1. Если обл. V разбить на две обл. и плоскостью, параллельной какой-либо из координатных плоскостей, то

Следствие: Если обл. V разбить на обл. ,

то

2. Теорема об оценке трёхкратного интеграла.

Если m, M – соответственно наименьшее и наибольшее значения функции в обл. V, то имеет место неравенство

,

где V – объём данной обл. V

3. Теорема о среднем.

Трёхкратный интеграл от непрерывной функции по обл. V равен произведению его объёма V на значение функции в некоторой точке Р обл. V, т. е.

Все свойства трехкратного интеграла доказываются аналогично как доказывают свойства двукратного интеграла.

Теорема: Тройной интеграл от функции по правильной обл. V равен трёхкратному интегралу по той же обл.

Доказательство аналогичное доказательству вычисления двойного интеграла.

Скобки в трёхкратном интеграле можно опустить и дифференциалы писать после каждого интеграла.

Пример: Найти массу тела, ограниченного координатными плоскостями и плоскостями x+y+z=2, x=1, y=1, если плотность тела задана формулой .

П остроим это тело.

Тело OACBEFD

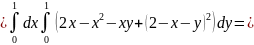
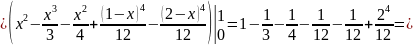
§9 Вычисление объёма тел с помощью тройного интеграла.

Пусть функция 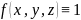во всех точках обл. V, тогда интегральная сумма

V – объём области V, ограниченной замкнутой поверхностью S.

Итак

П ример: Найти объём тела, ограниченного координатными плоскостями, плоскостью 2x+3y-6=0 и цилиндром z=

§10 Замена переменных в тройном интеграле.

1. Общая замена переменных в тройном интеграле.

Пусть функции

взаимно однозначно отображают обл. V в декартовых координатах на обл. V’ в криволинейных координатах .

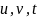Тогда

где - якобиан перехода и численно равен определителю третьего порядка

2. Т ройной интеграл в цилиндрических координатах.

П оложение т. Р в цилиндрических координатах определяется 3^мя числами φ, ρ, z, где φ, ρ – полярные координаты проекции т. Р на плоскость xoy, z – аппликата т. Р, т.е. расстояние т. Р от плоскости xoy.

Связь между декартовыми и цилиндрическими координатами:

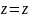
Якобиан перехода будет равен:

Тогда