3.4 Прямая в пространстве
Система двух уравнений, каждое из которых задает плоскость
(3.15)
определяет в пространстве прямую как линию пересечения этих плоскостей. Уравнения (3.15) называются общими уравнениями прямой.
Пусть прямая проходит через точку
параллельно направляющему вектору
(рис. 3.11).
Т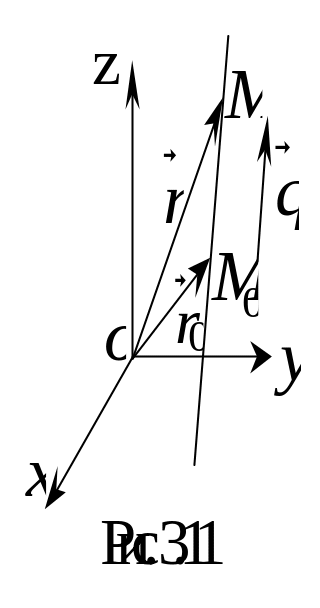
очно
так же, как это делалось для прямой на
плоскости, строятся векторное,
параметрические и канонические уравнения
прямой в пространстве (при этом
любое действительное
число):
векторное уравнение, (3.16)
параметрические уравнения, (3.17)
канонические уравнения. (3.18)
Заметим, что каждое из канонических уравнений
определяет плоскость, параллельную,
соответственно,
и
а сама прямая является линией пересечения
этих плоскостей, причем среди канонических
уравнений только два независимых.
П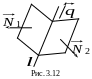
ример
3.16. Прямая
задана общими уравнениями
Составить ее канонические уравнения.
Решение. Рассмотрим
и
нормали к плоскостям,
пересечение которых, согласно заданным
общим уравнениям дает прямую
(рис. 3.12). Поскольку
и
перпендикулярны
то в качестве направляющего вектора
этой прямой можно взять
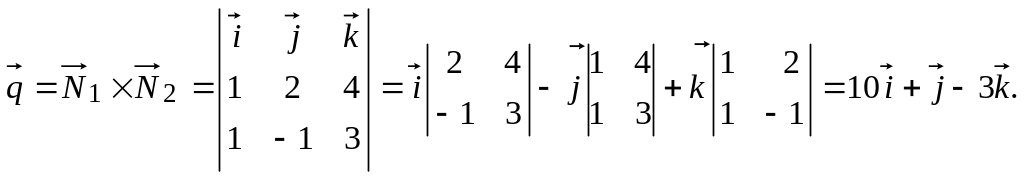
Для того, чтобы выбрать какую-нибудь
точку
на прямой
придадим одной из координат произвольное
значение, например,
,
а две другие найдем, решив систему
Опуская выкладки, запишем ее решение:
т.е.
Итак, каноническими уравнениями прямой
будут:
Пример 3.17. Написать уравнения прямой,
проходящей через две точки:
и
Решение. Искомая прямая проходит
через точку
при этом ее направляющий вектор
Таким образом, ее канонические и общие
уравнения имеют вид
Определение. Углом между двумя прямыми и в пространстве называется один из двух смежных углов, которые образуют прямые, проведенные параллельно данным через какую-либо точку пространства (рис. 3.13).
П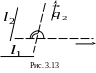
усть
и
направляющие
векторы прямых
и
,
тогда
,
причем
(3.19)
Заметим, что для неперпендикулярных
прямых
,
вычисленный по этой формуле, может
оказаться больше или меньше нуля (угол
может быть острым или тупым) в зависимости
от выбранных направлений
и
вдоль соответствующих прямых.
Прямые
и
будут параллельны, если
т.е.
и перпендикулярны, если
т.е.
Пример 3.18. Найти угол между прямыми
Решение. Поскольку направляющие
векторы прямых:
то
3.5 Прямая и плоскость в пространстве
Определение. Углом между прямой и плоскостью называется один из двух смежных углов между прямой и ее проекцией на плоскость (последняя является линией пересечения с плоскостью, проходящей через перпендикулярно , рис. 3.14).
Е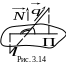
сли
и
соответственно
нормаль к
и направляющий вектор прямой
,
то справедлива формула
при этом
(3.20)
Заметим, что
при
при
Пример 3.19. Даны прямая
и плоскость
Найти угол
между ними и координаты точки их
пересечения.
Решение.
1)
2) Координаты точки пересечения найдем из системы
которую легко решить, введя параметр
и используя параметрические уравнения
прямой
Подставляя
из первых трех уравнений в четвертое,
получим
откуда
и, следовательно, из первых трех уравнений
найдем координаты точки M:
Таким образом,
Пример 3.20. Составить уравнение плоскости
,
проходящей через точку
и параллельной прямым
и
Решение. Поскольку вектор нормали
к плоскости
перпендикулярен обеим прямым, т.е. их
направляющим векторам, то выберем
где
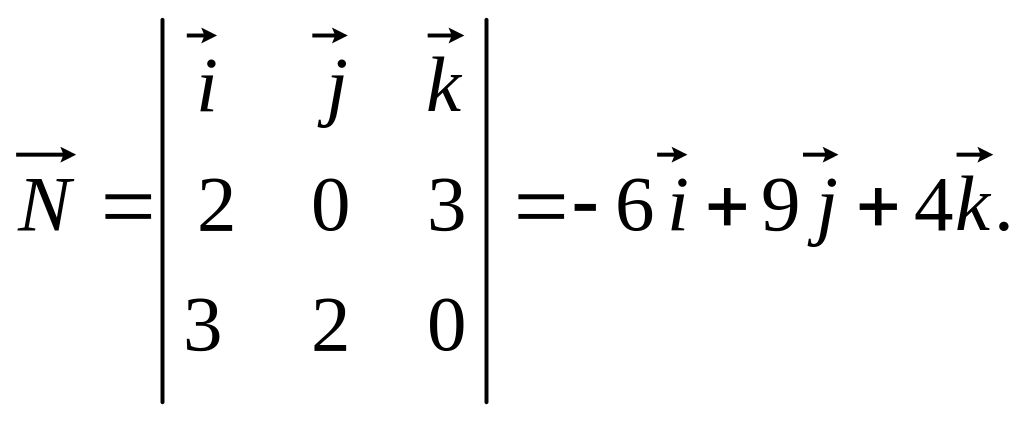Уравнением плоскости
будет
или
