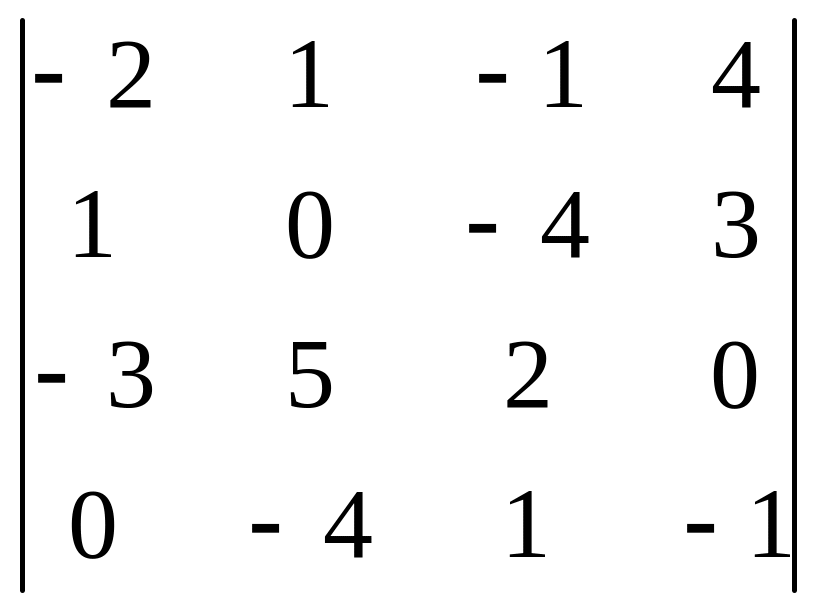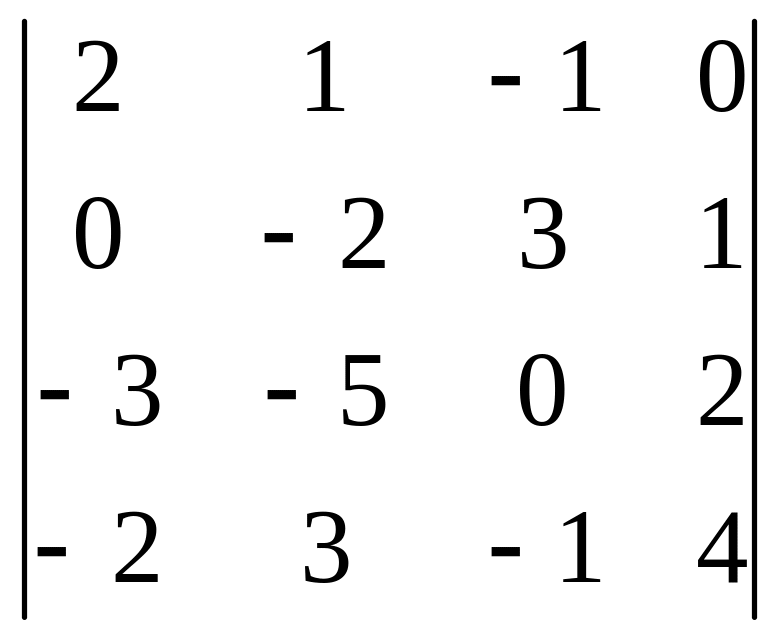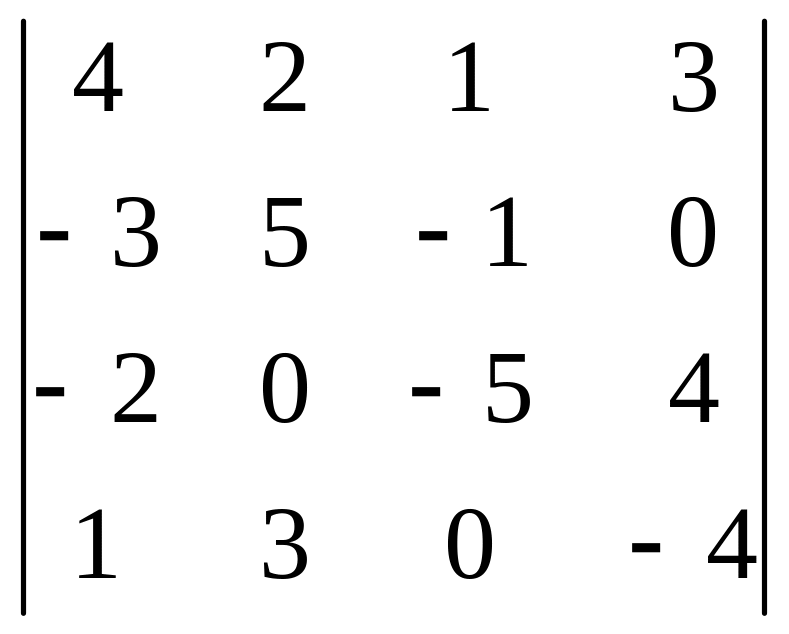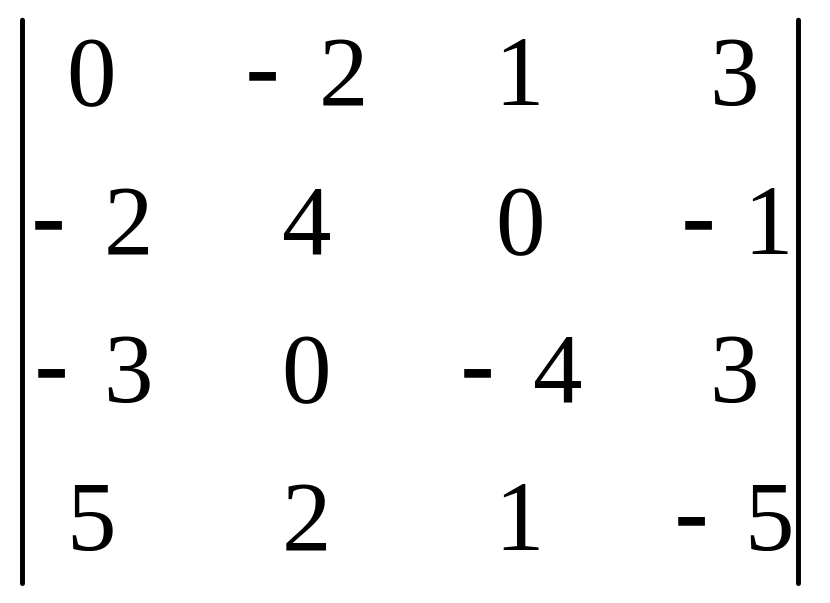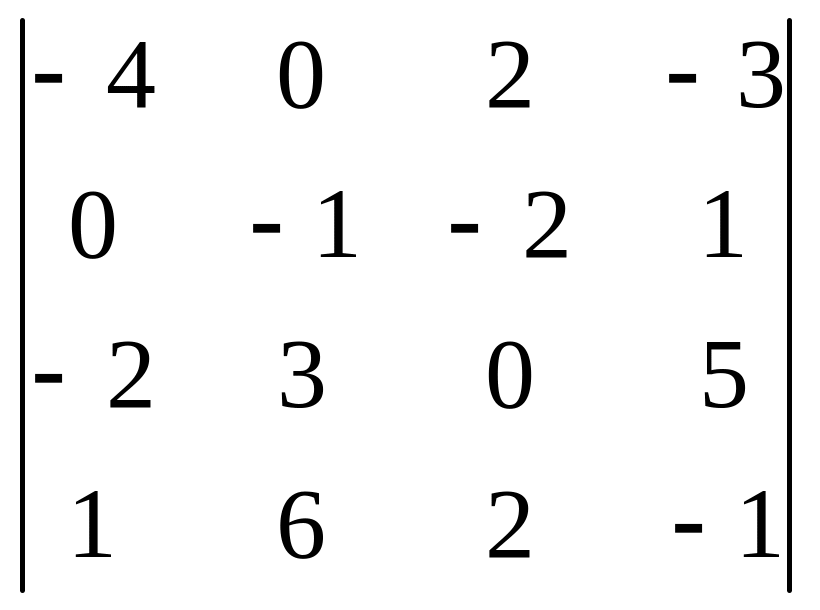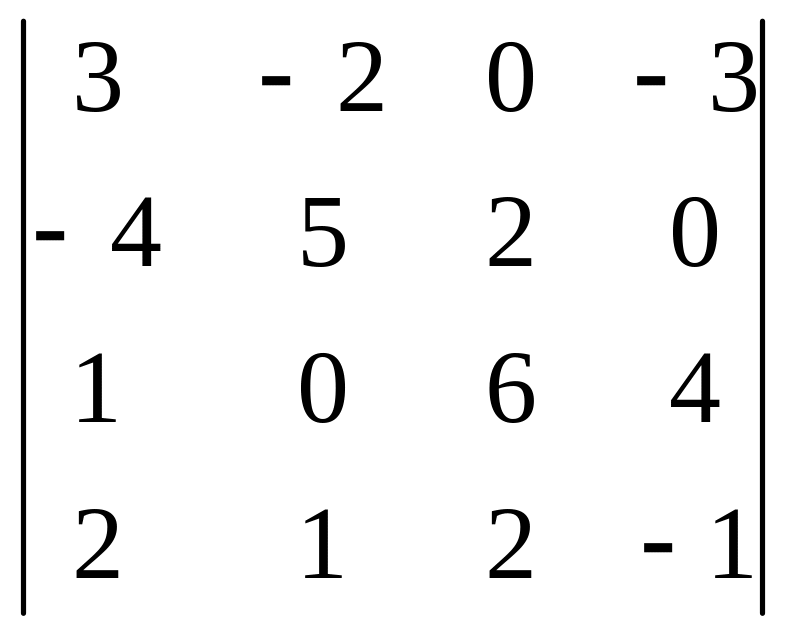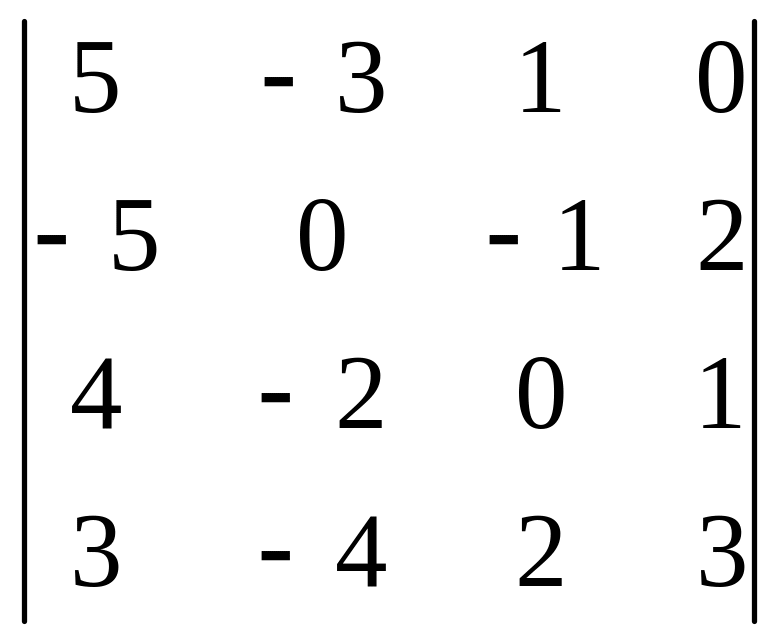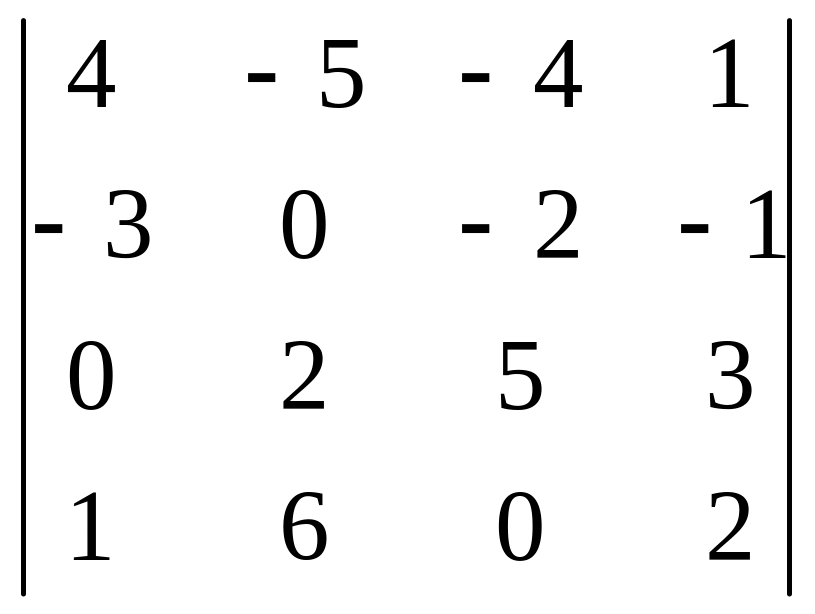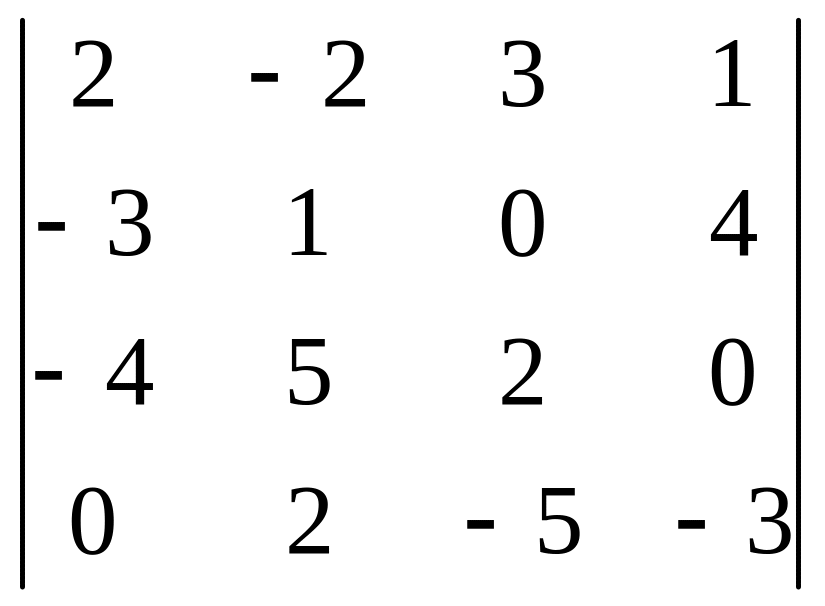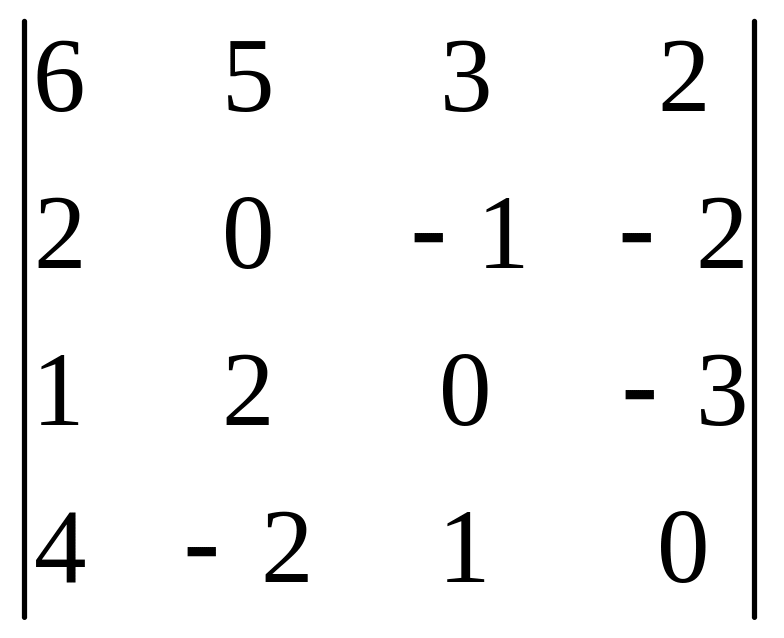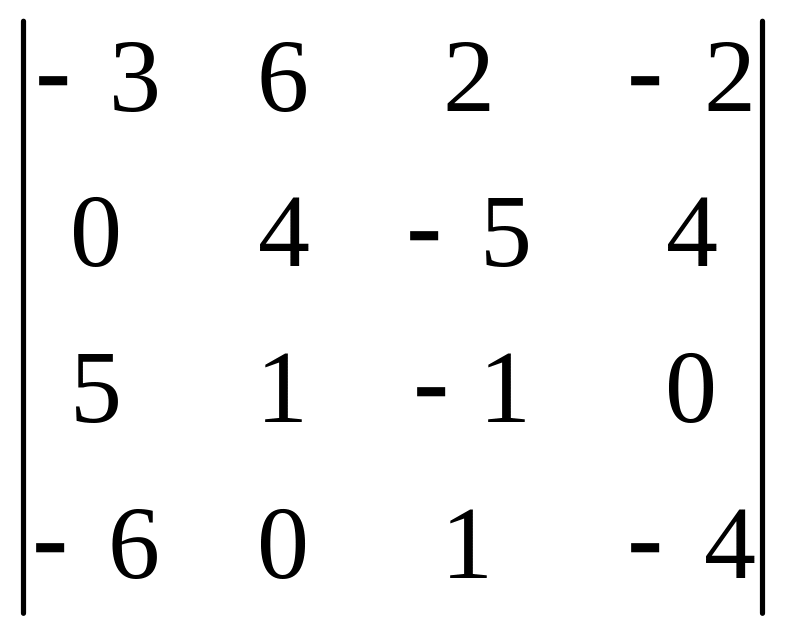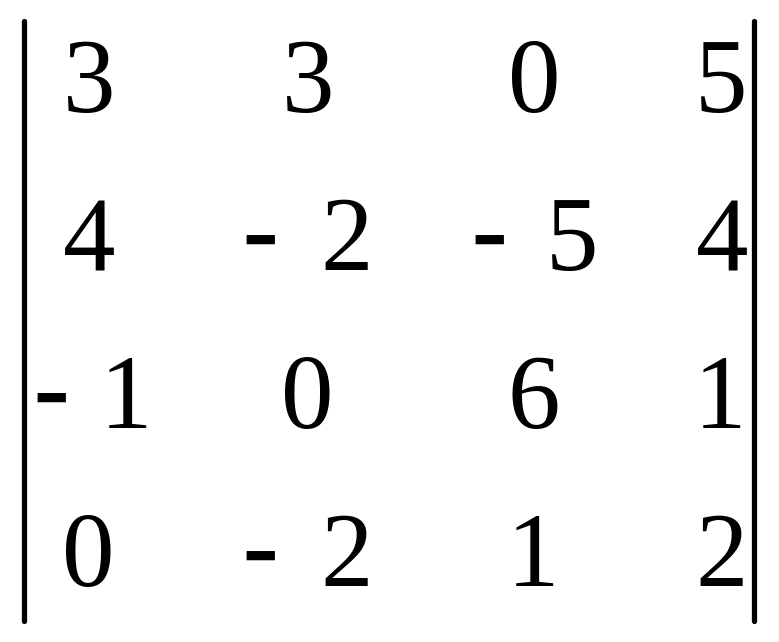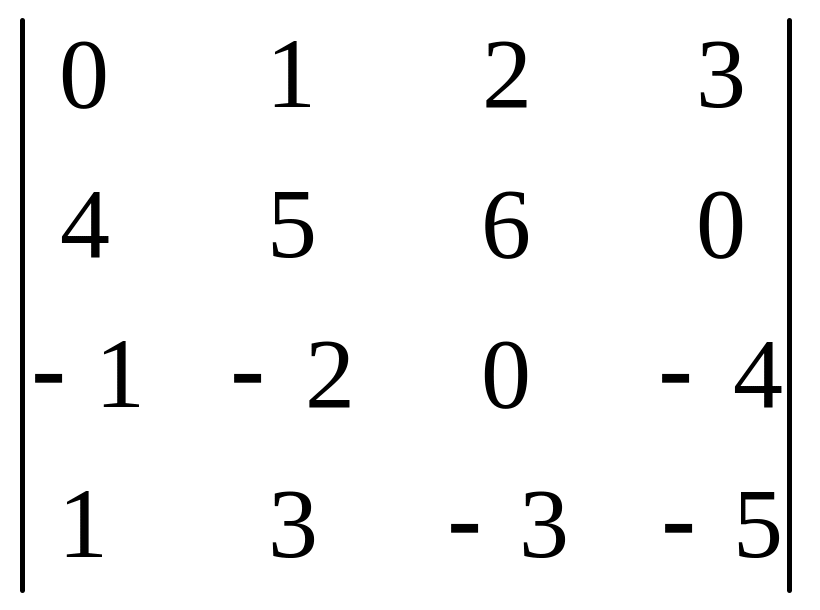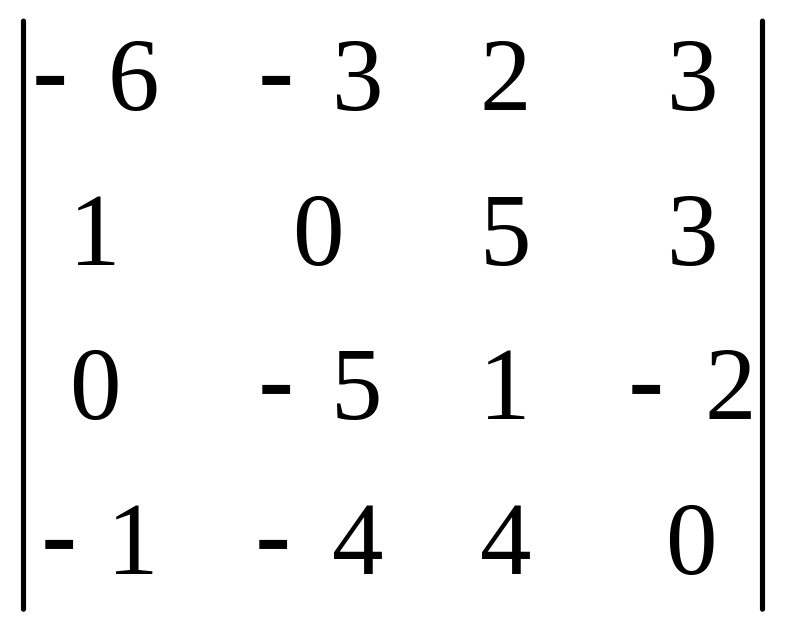Варианты заданий для самостоятельного решения
Элементы теории систем линейных уравнений, матриц и определителей
1. Решить систему линейных уравнений методом Гаусса.
01) |
02)
|
03) |
04) |
05) |
06) |
07) |
08) |
09) |
10) |
11) |
12) |
13) |
14) |
15) |
16) |
|
|
2 . Вычислить определитель четвертого порядка:
а) с помощью разложения по элементам любой строки;
б) с помощью разложения по элементам любого столбца;
в) с помощью преобразования исходной матрицы в матрицу треугольного вида.
01)
|
02)
|
03)
|
04)
|
05)
|
06)
|
07)
|
08)
|
09)
|
10)
|
11)
|
12)
|
13)
|
14)
|
15)
|
16)
|
3. Решить систему линейных уравнений с помощью правила Крамера.
01) |
02) |
03) |
04) |
05) |
06) |
07) |
08) |
09) |
10) |
11) |
12) |
13) |
14) |
15) |
16) |
|
|
4. Самостоятельно выбрать три квадратные матрицы второго порядка и проверить справедливость предлагаемых равенств
5. Записать систему линейных уравнений из п.3 в виде матричного уравнения и решить ее методом обратной матрицы. Сравнить результат с результатом, полученным по правилу Крамера.
6. Решить матричные уравнения
где
заданные
квадратные матрицы второго порядка, а
– неизвестные матрицы.
-
01)
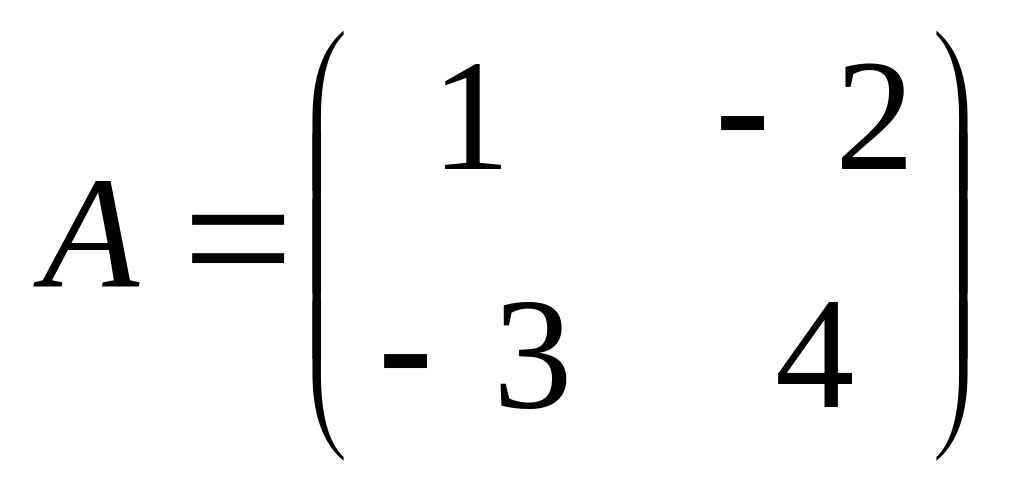
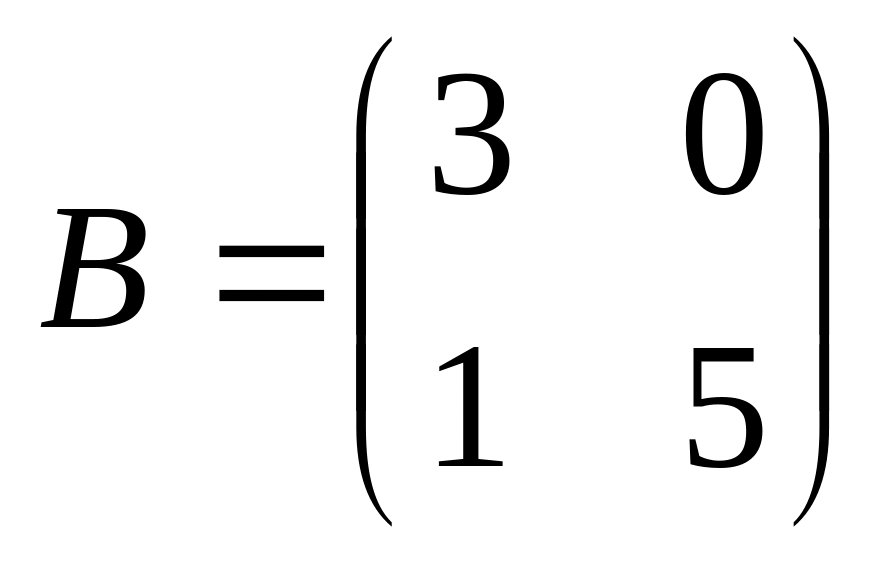
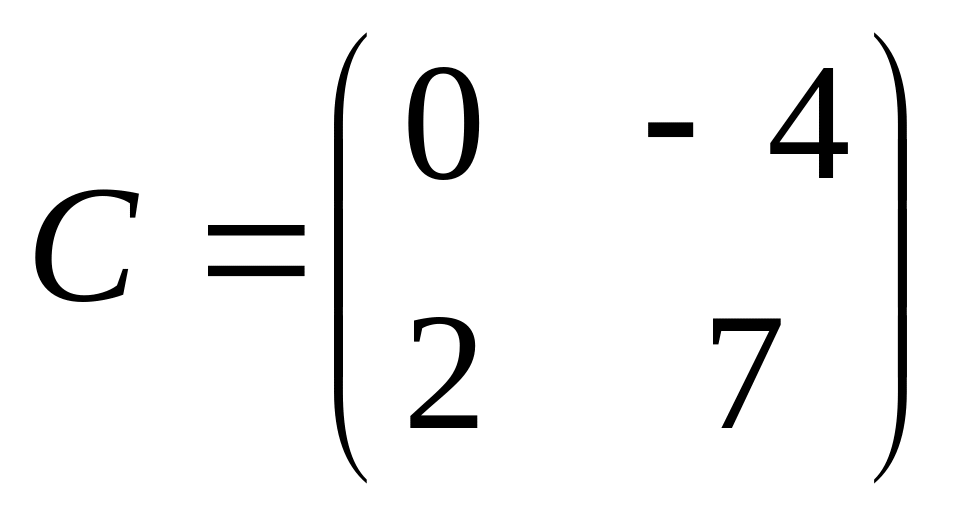
02)
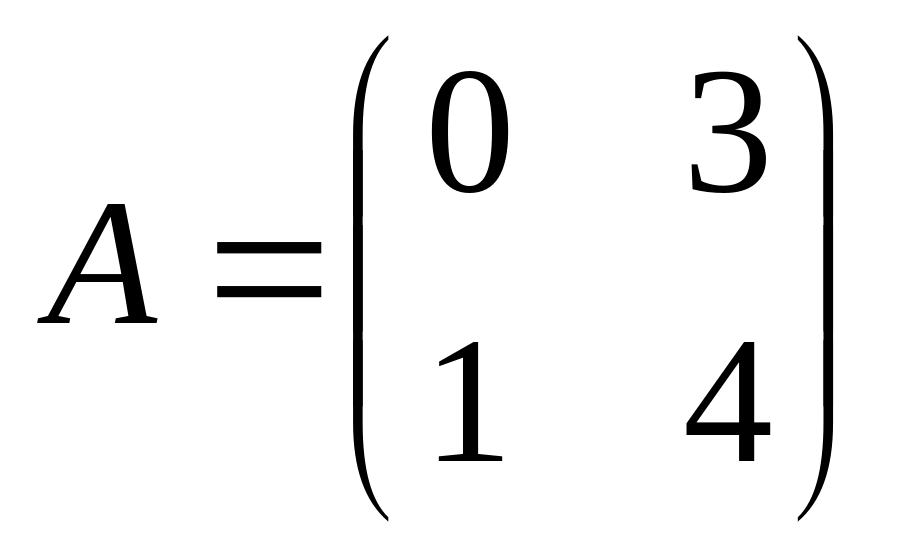
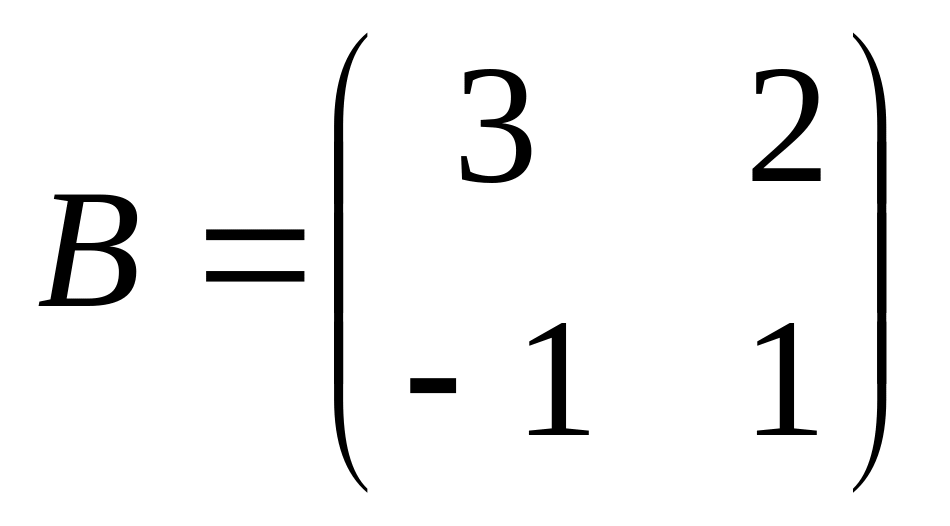
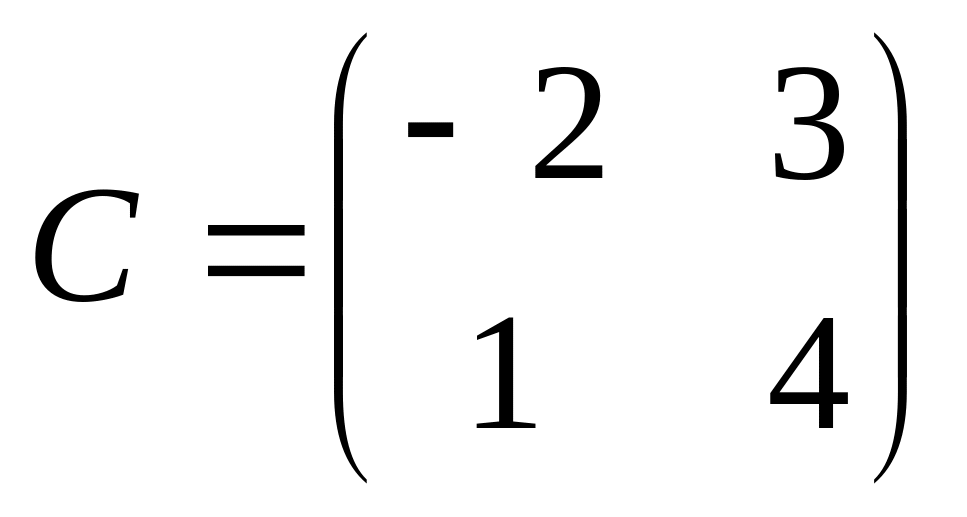
03)
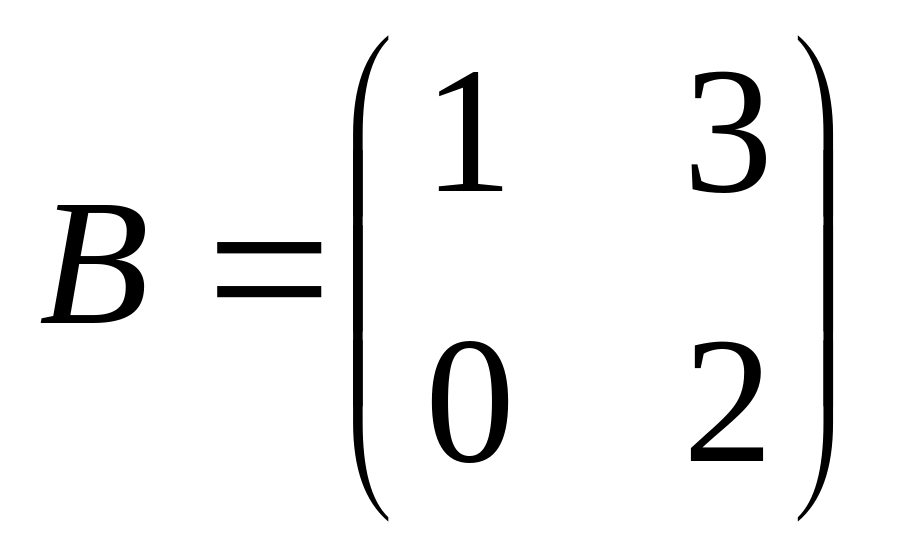
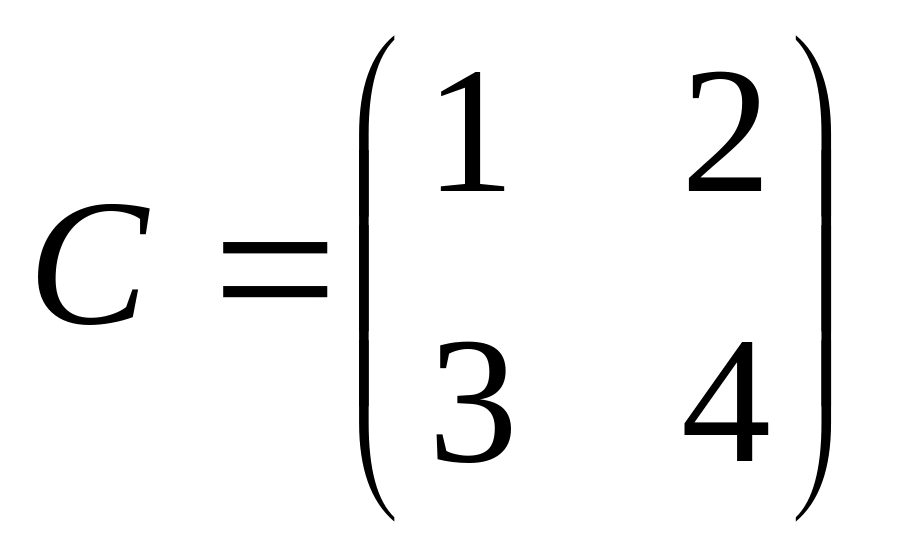
04)
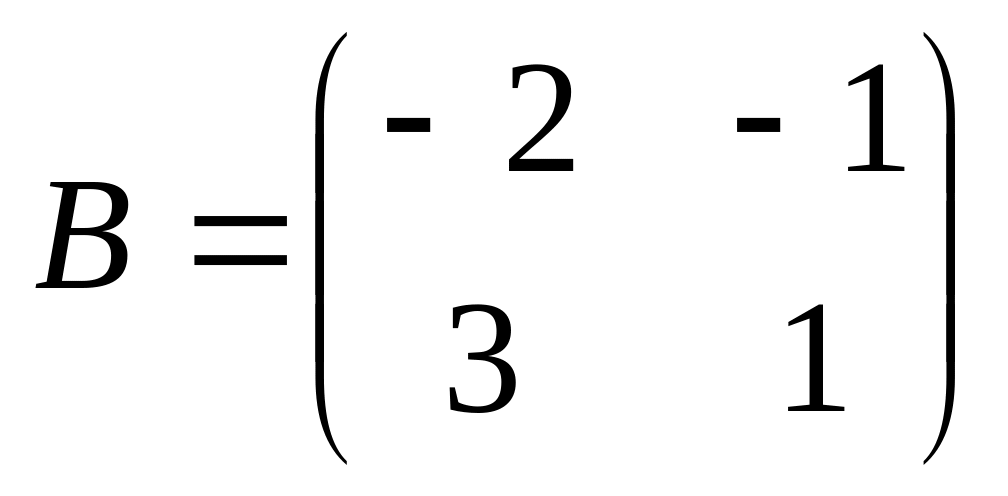
05)
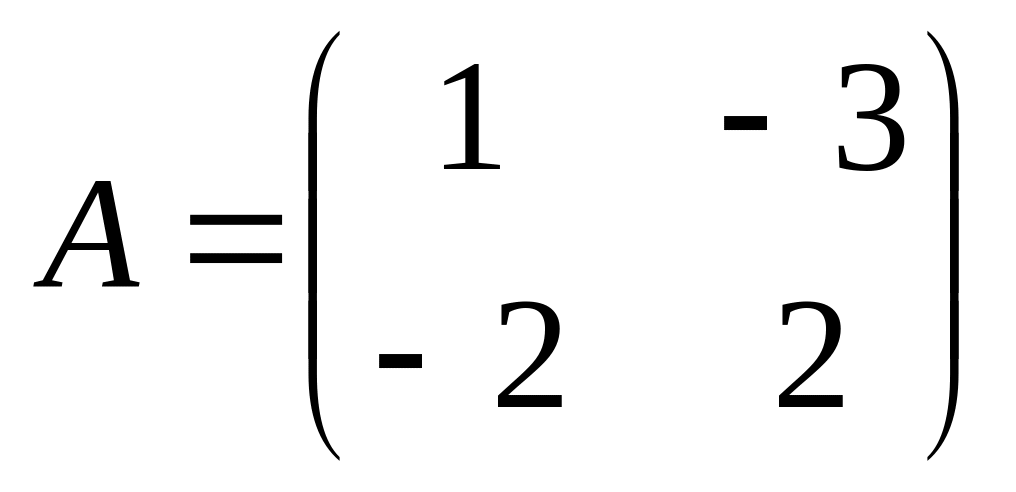
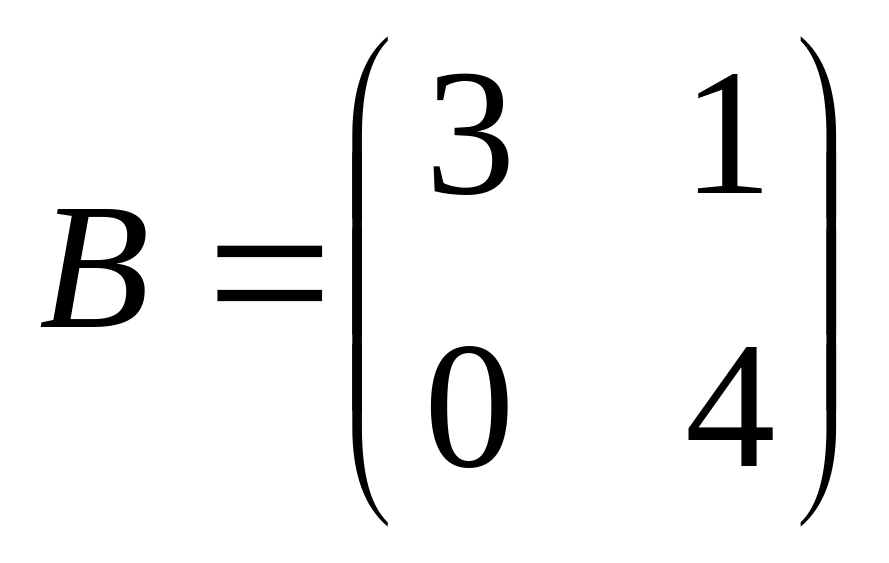
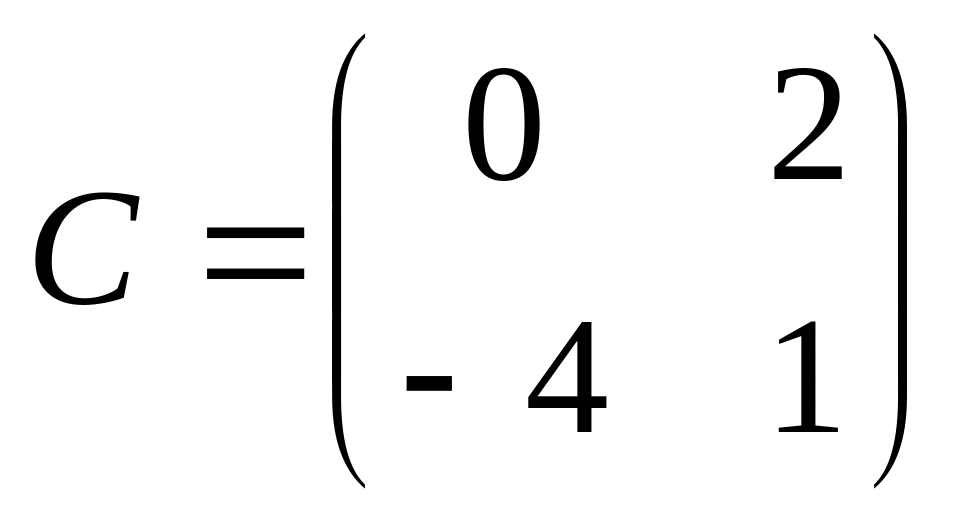
06)
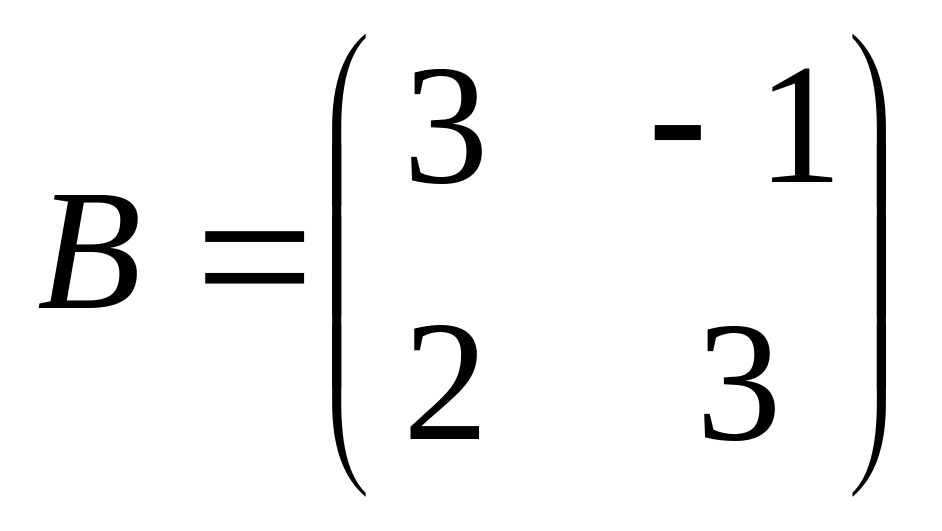
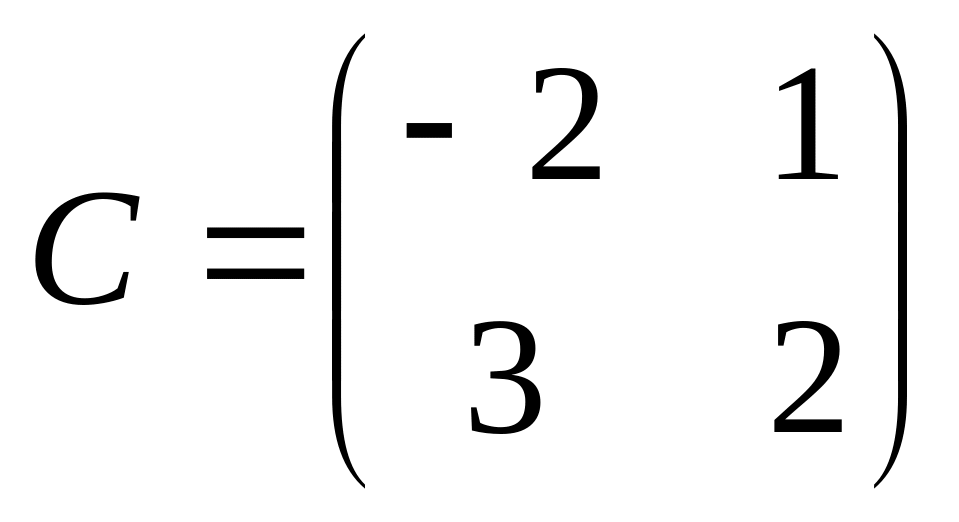
07)
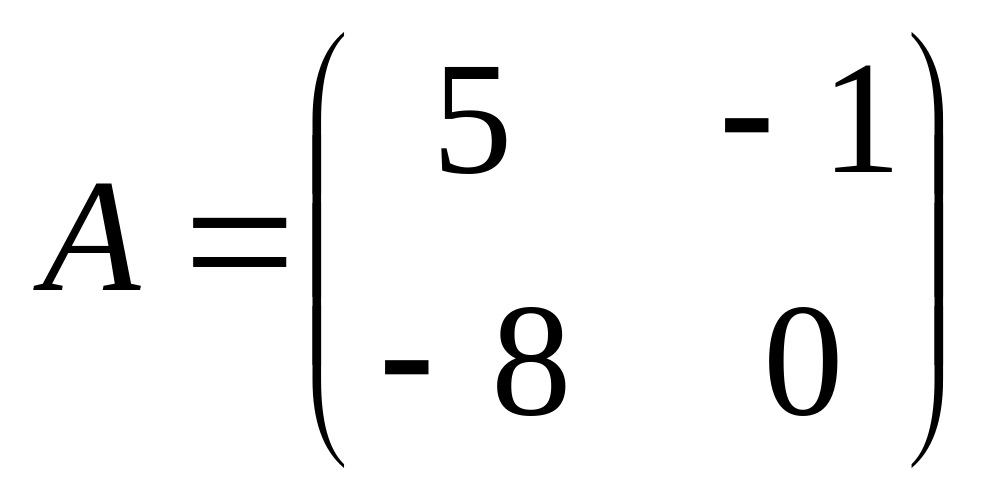
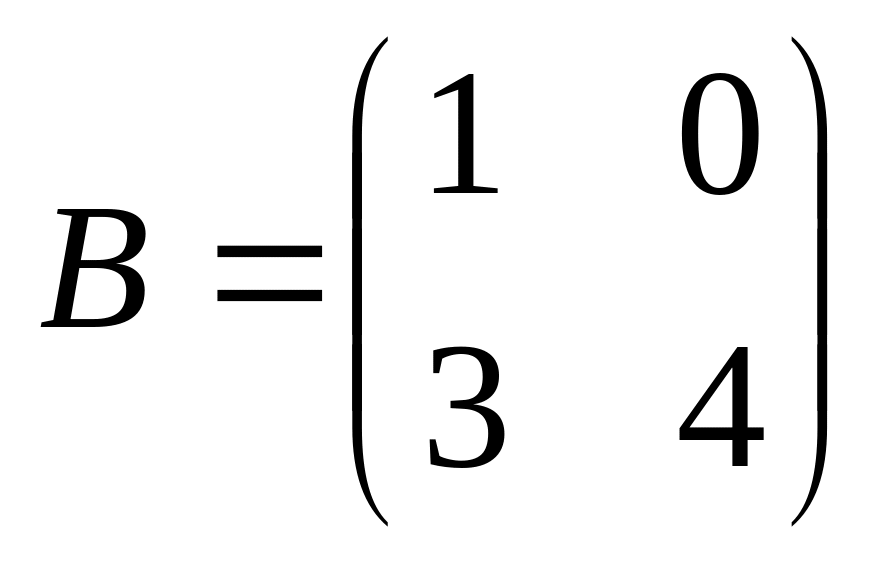
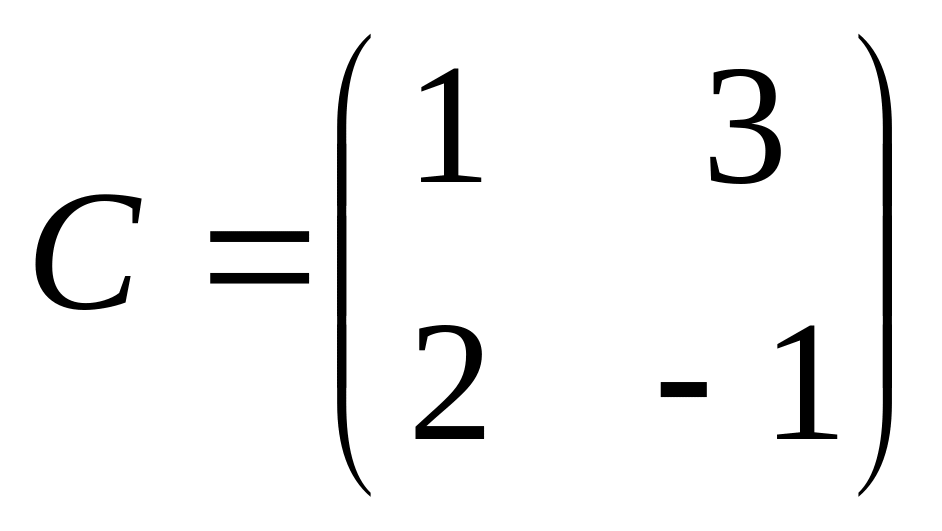
08)
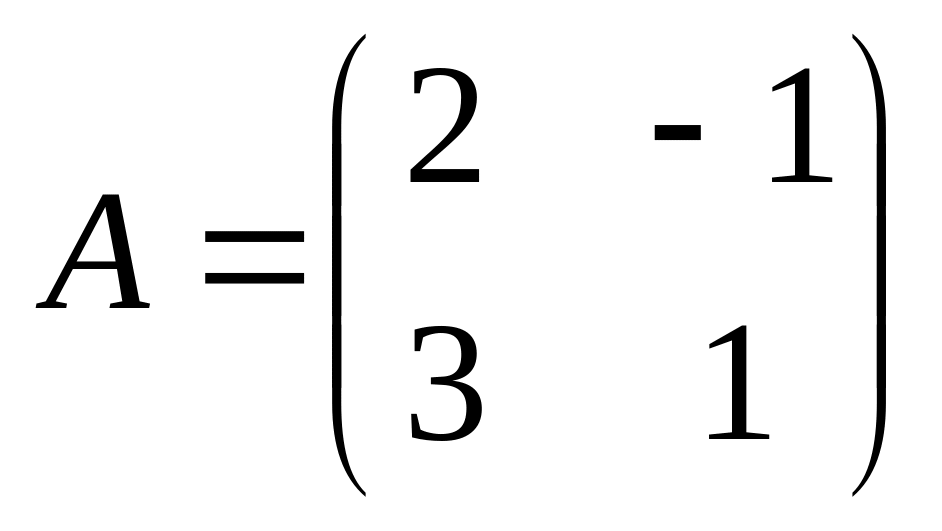
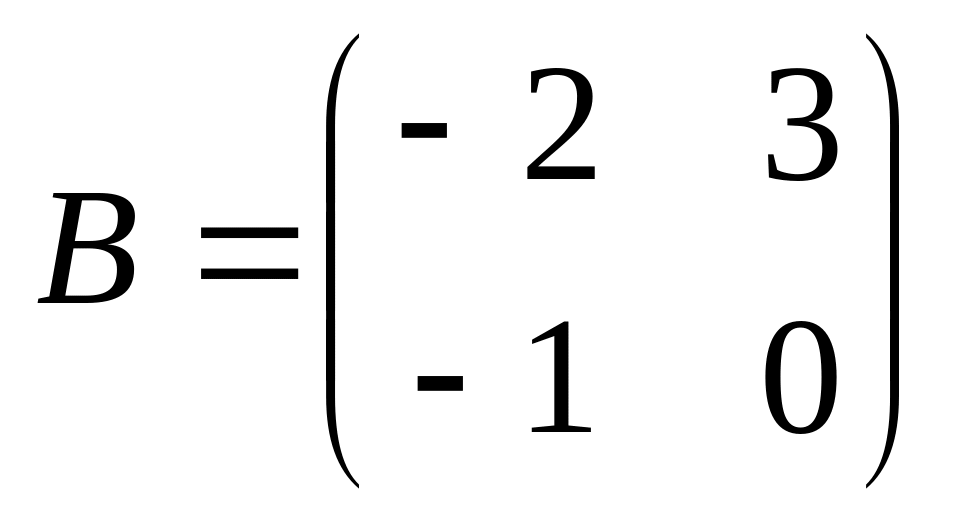
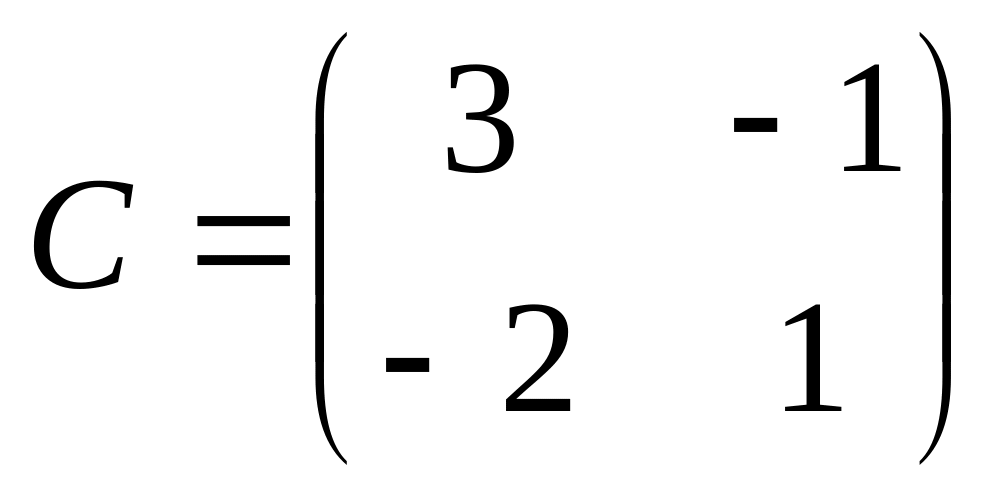
09)
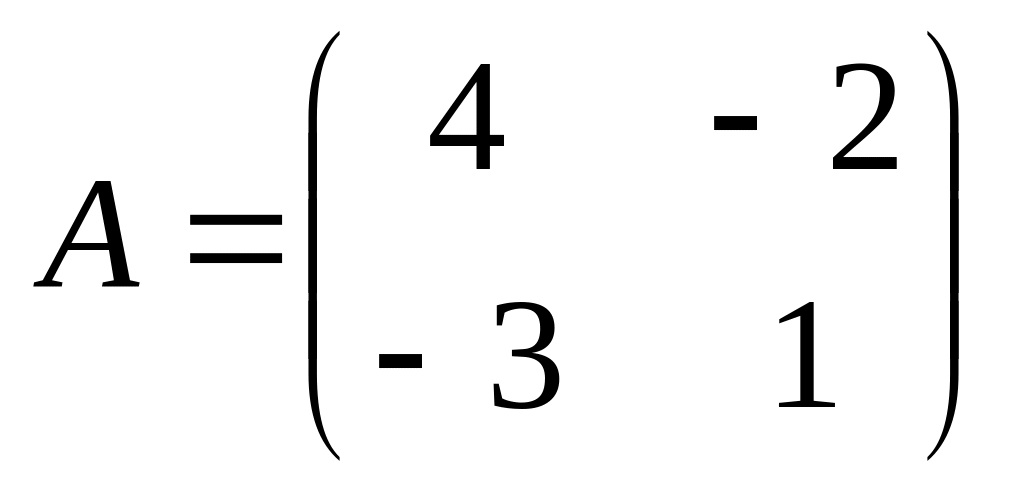
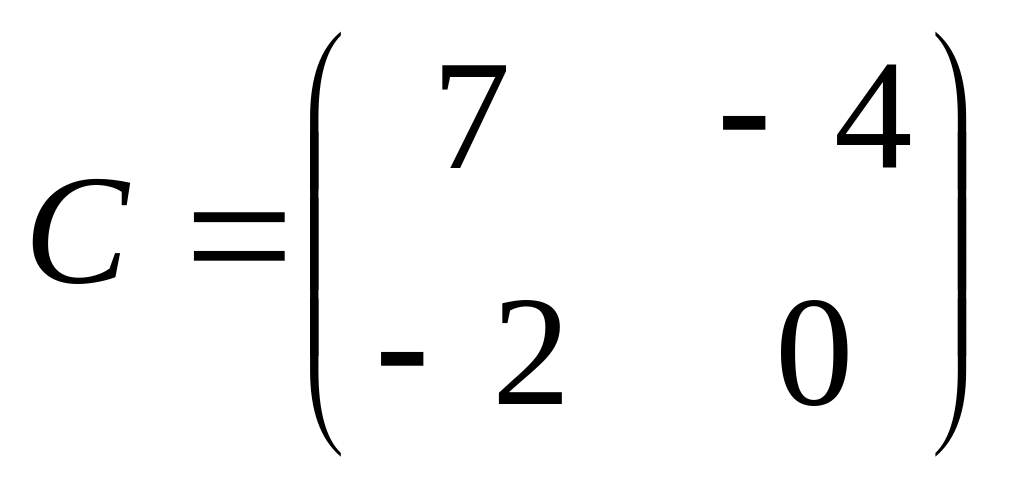
10)
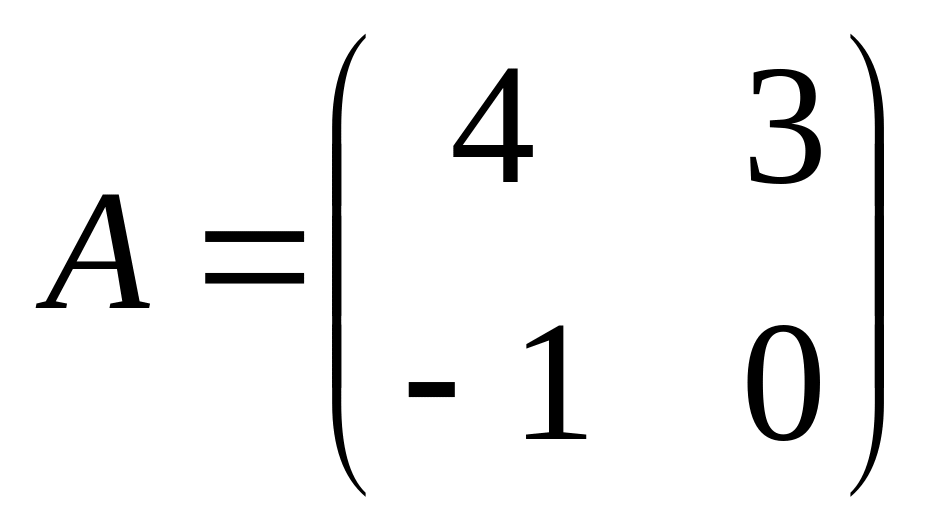
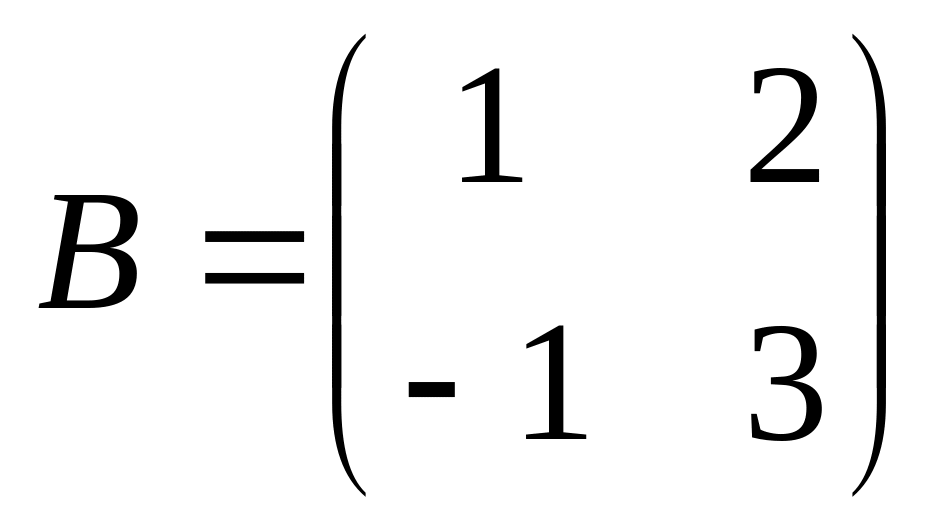
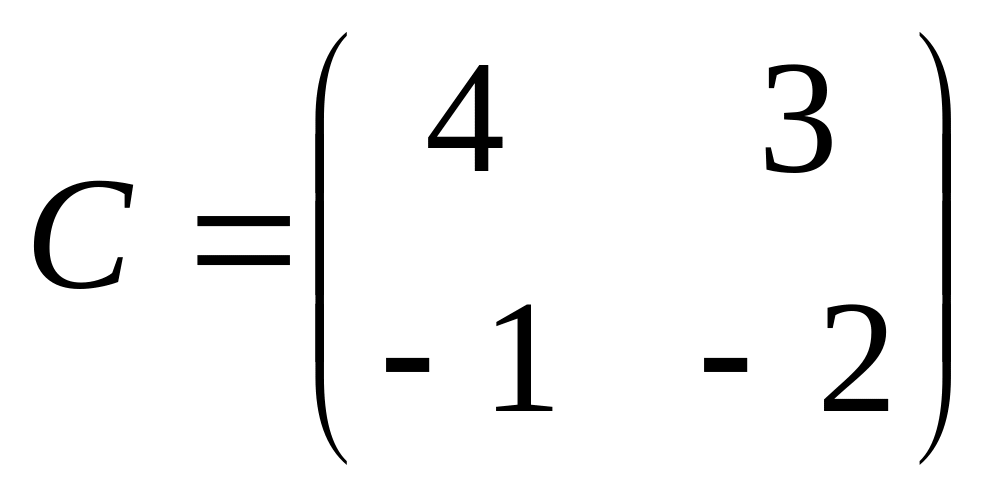
11)
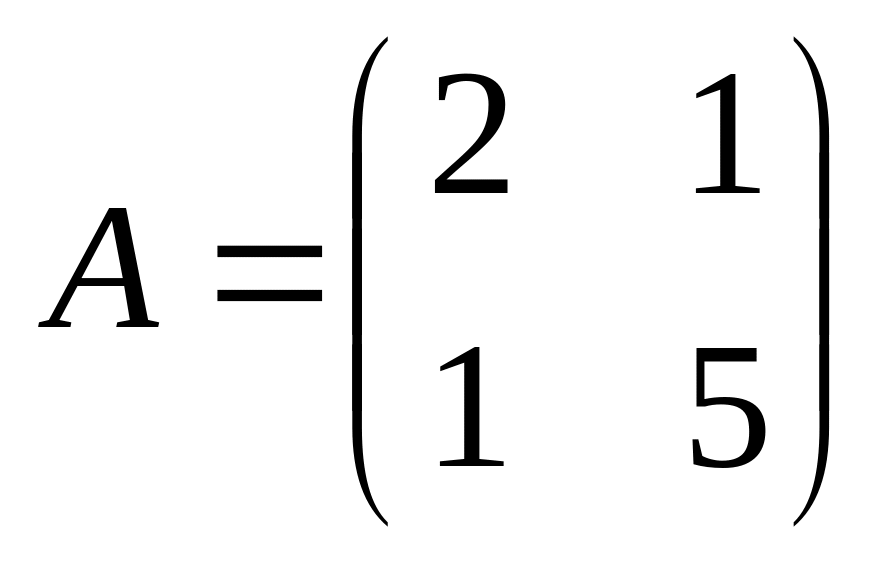
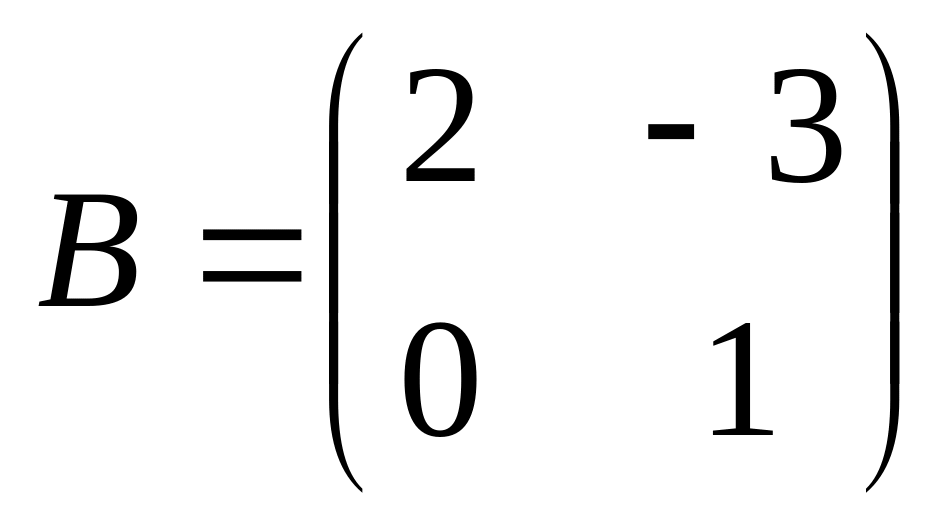
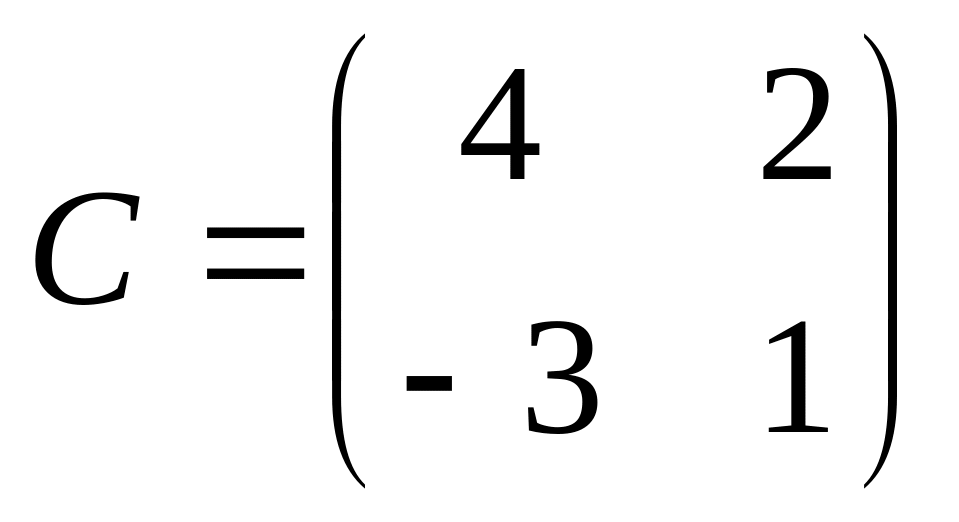
12)
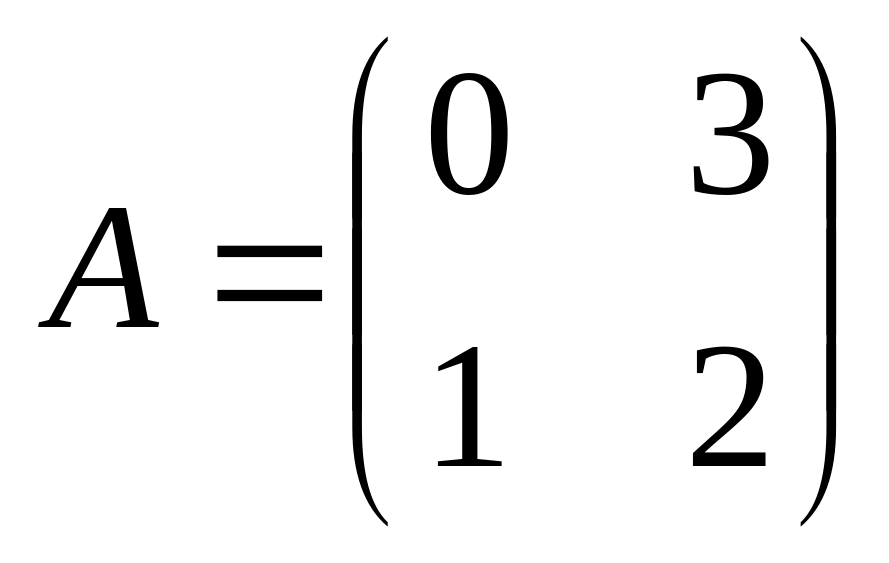
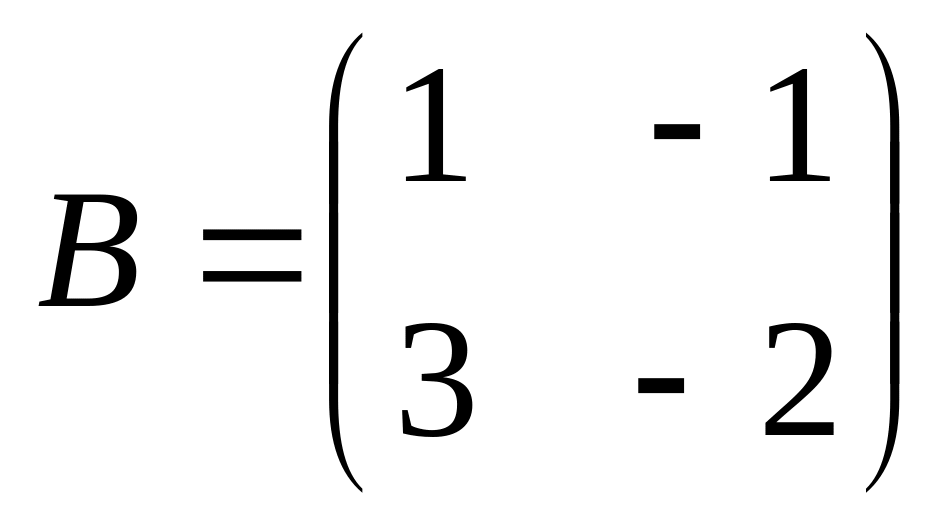
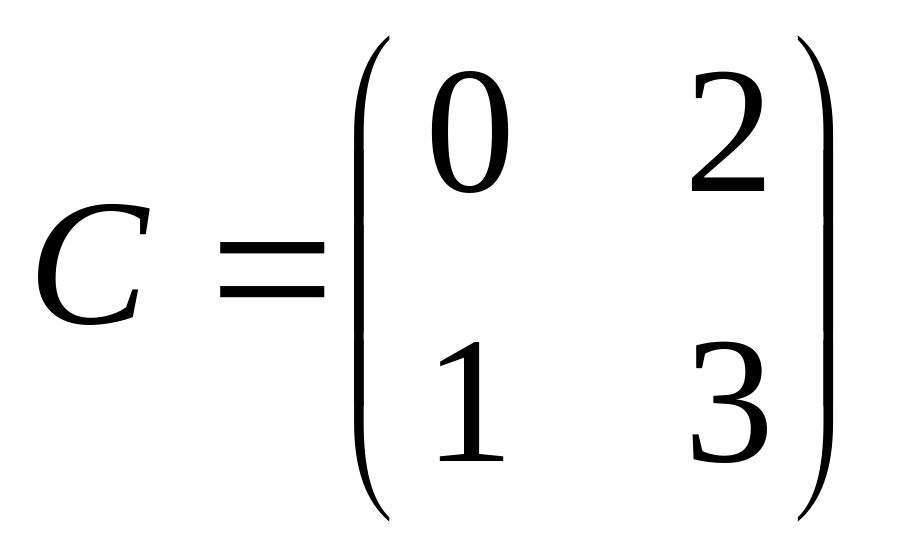
13)
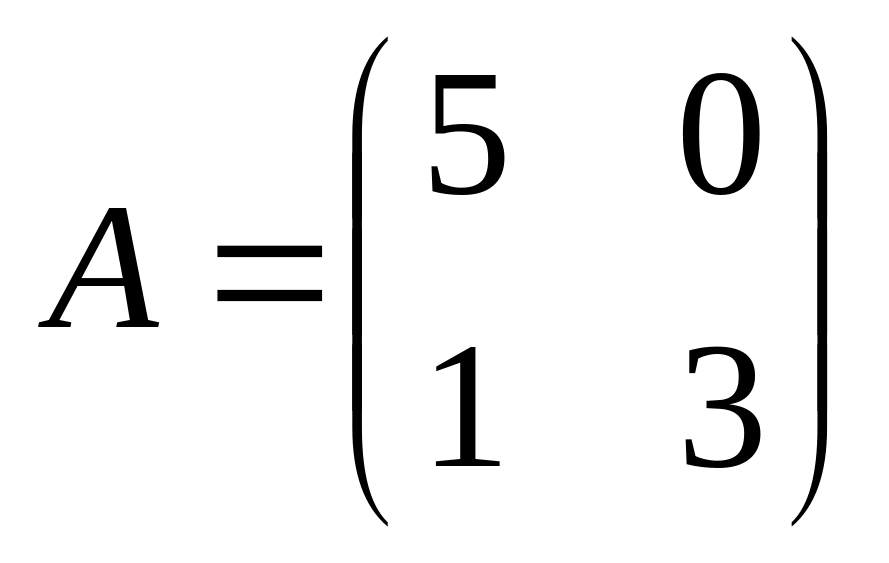
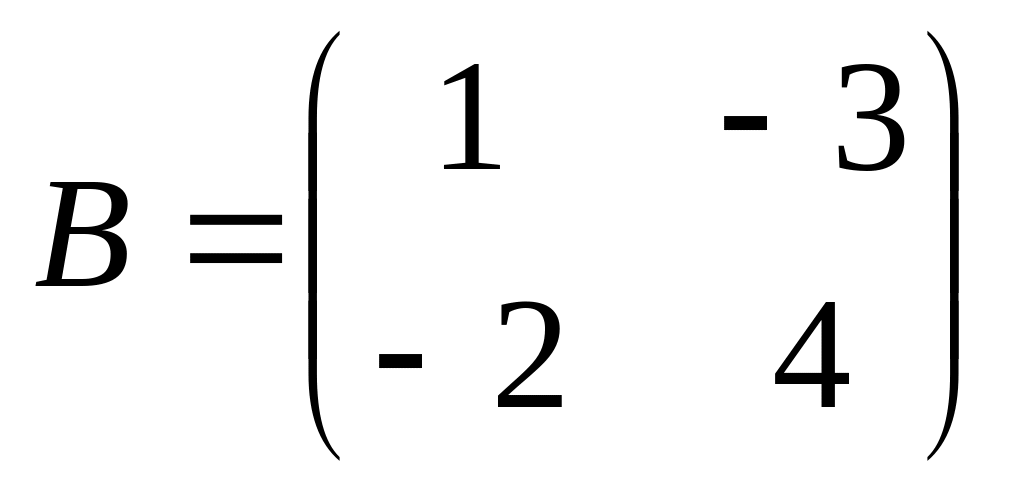
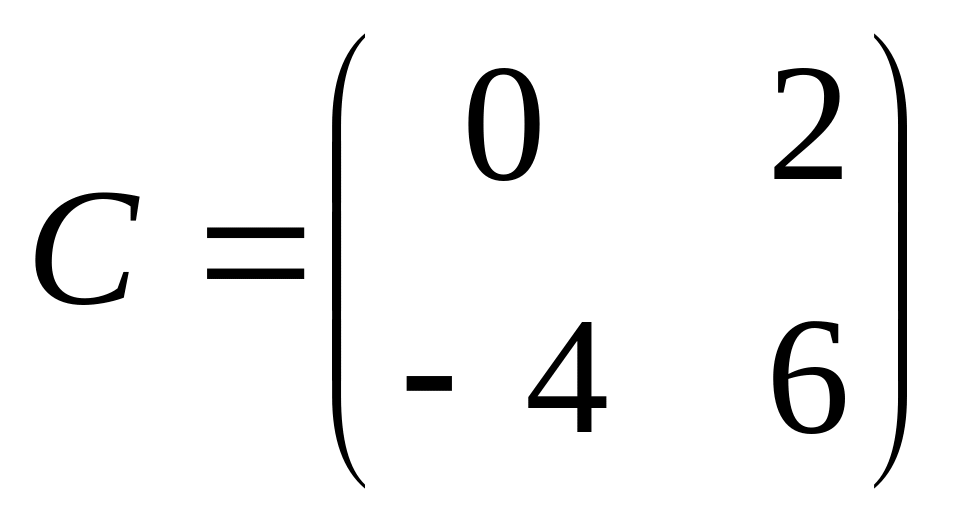
14)
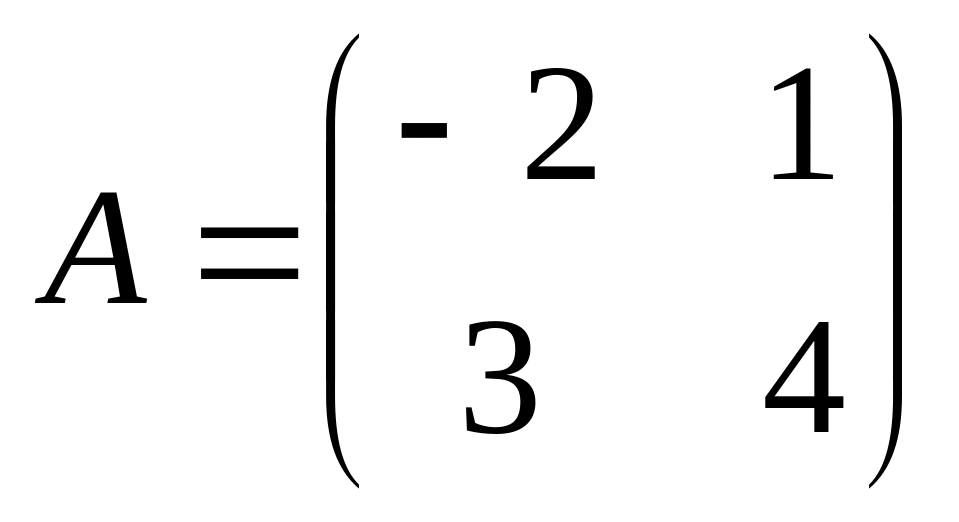
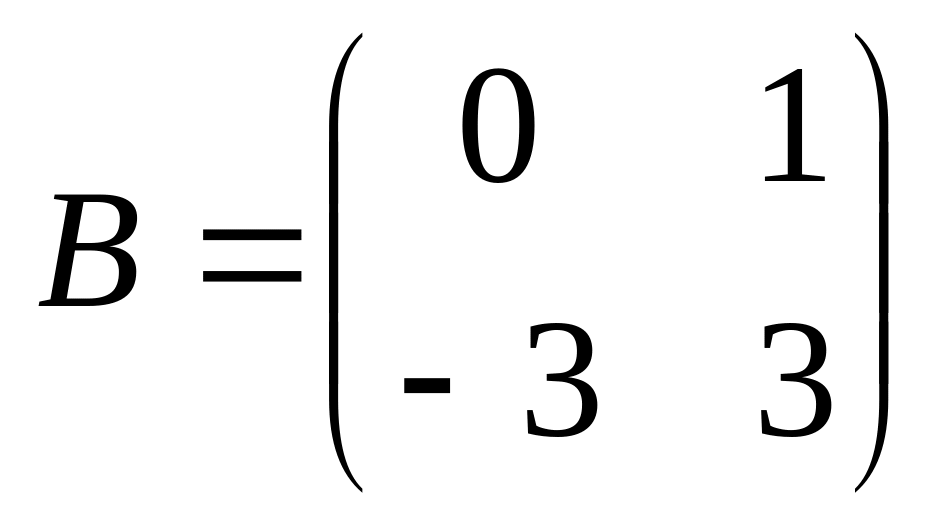
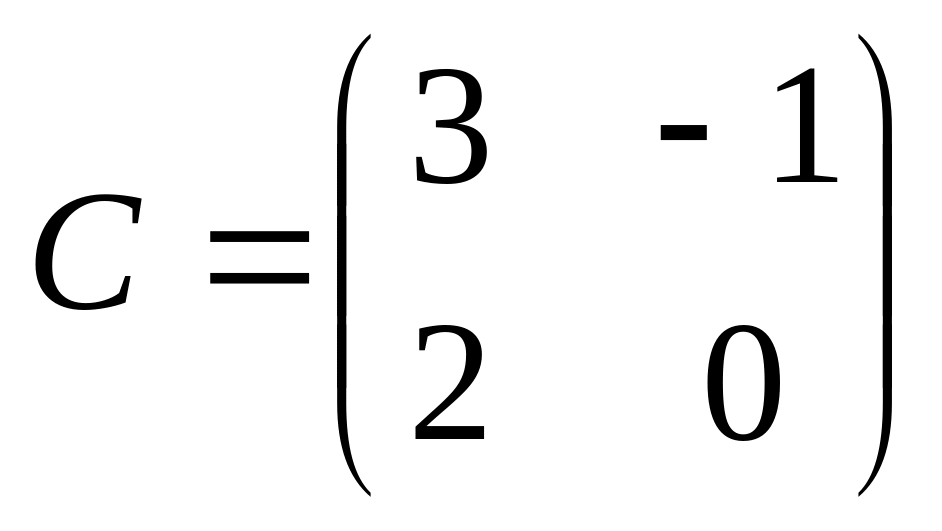
15)
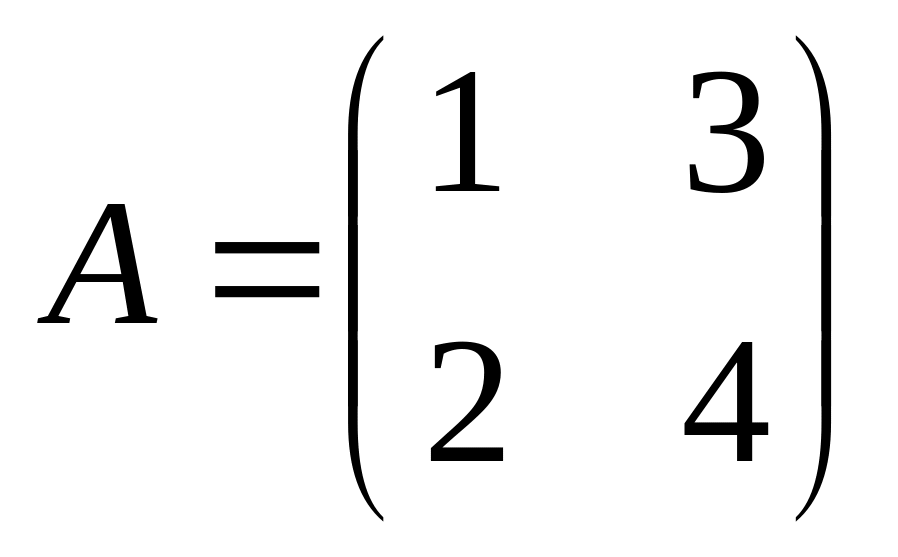
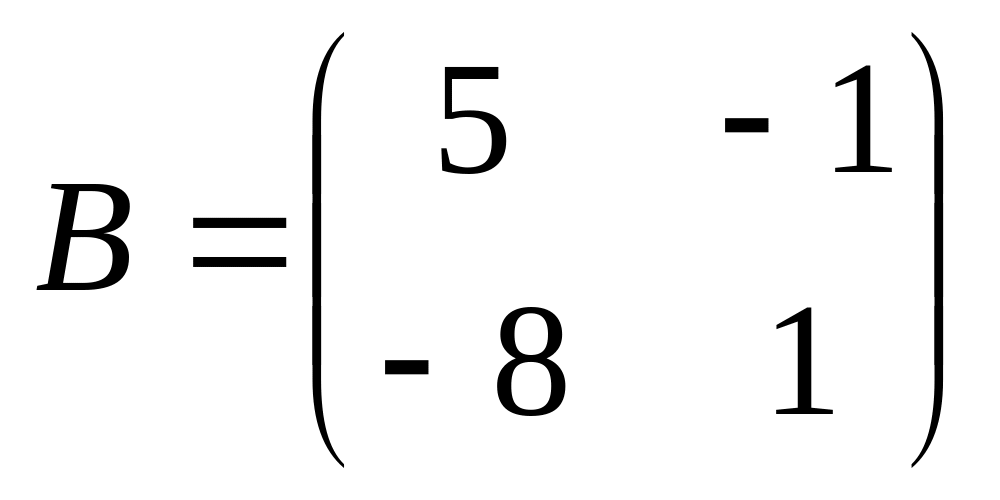
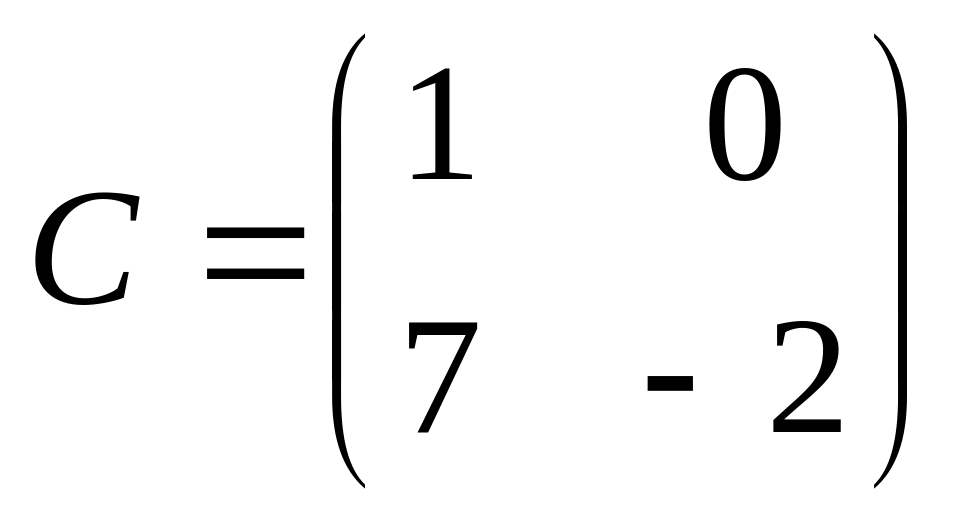
16)
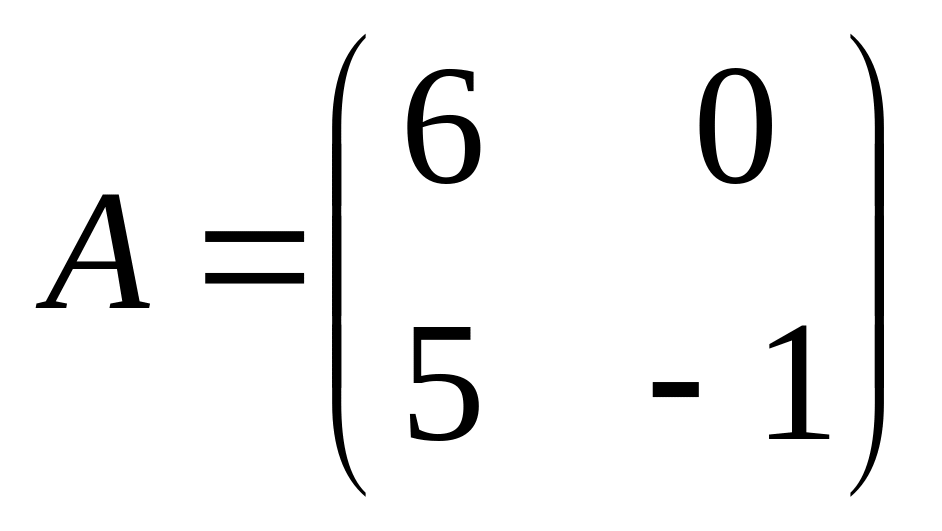
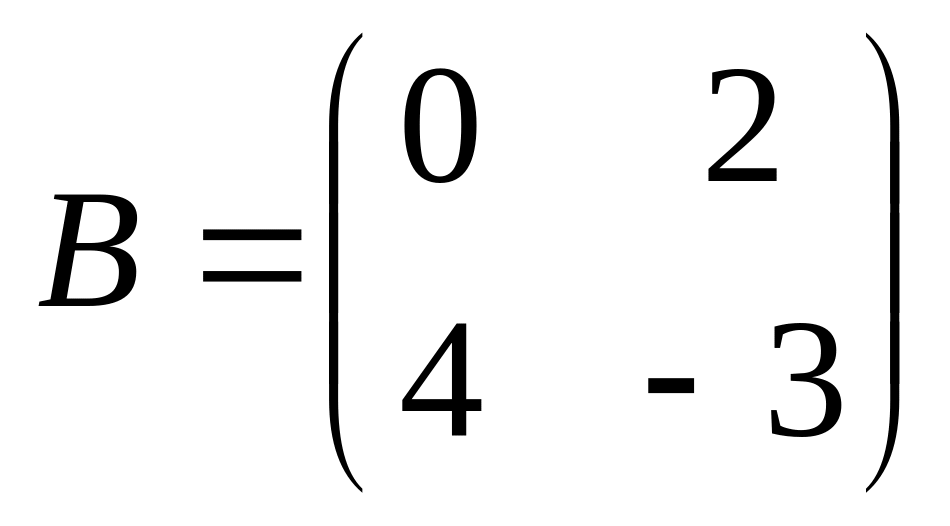
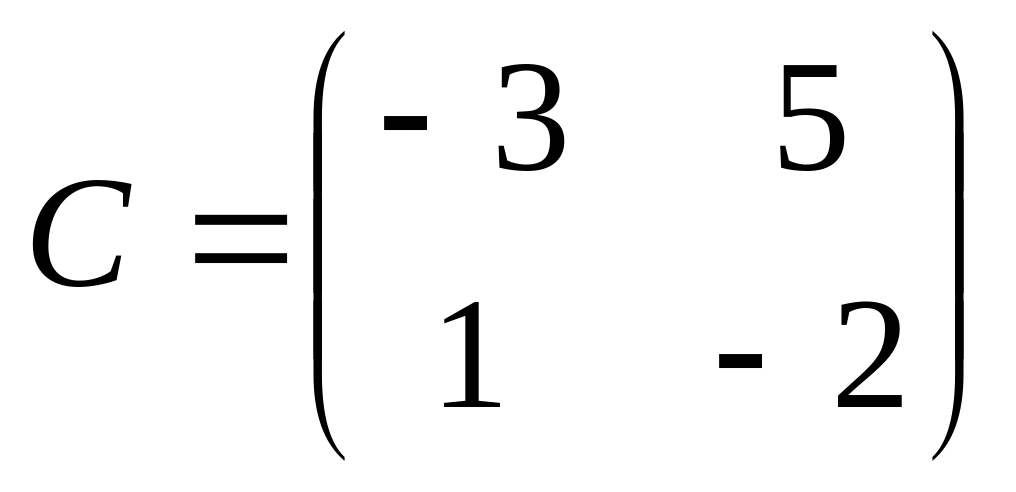
Элементы векторной алгебры
7. Указать значения величин и β, при которых векторы и коллинеарны.
01)
|
|
02)
|
|
03)
|
|
04)
|
|
05)
|
|
06)
|
|
07)
|
|
08)
|
|
09)
|
|
10)
|
|
11)
|
|
12)
|
|
13)
|
|
14)
|
|
15)
|
|
16)
|
|
8. Треугольник задан своими вершинами. Найти:
а) длину медианы
проведенной из вершины
б) угол между медианой
и стороной
в) координаты точки
пересечения медиан треугольника.
01)
02)
03)
04)
05)
06)
07)
08)
09)
10)
11)
12)
13)
14)
15)
16)
9. Установить, лежат ли четыре точки
в одной плоскости. Варианты значений
координат точек
взять из заданий п. 8
-
01)
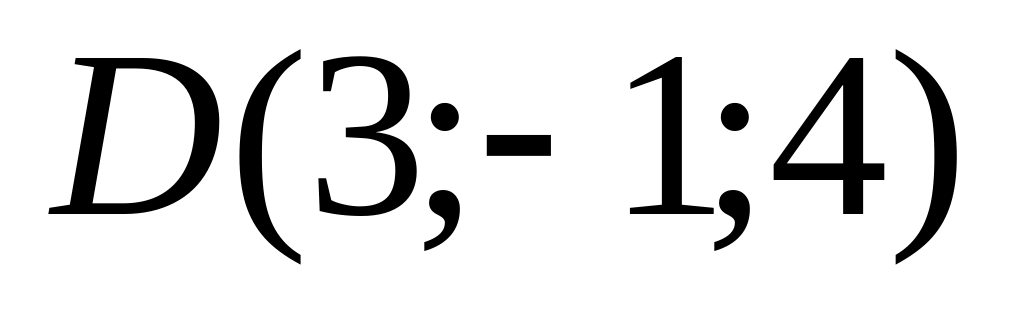
02)
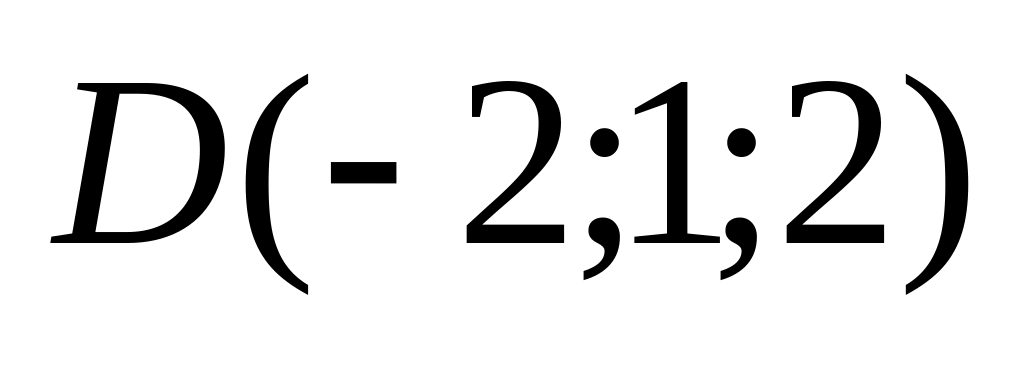
03)
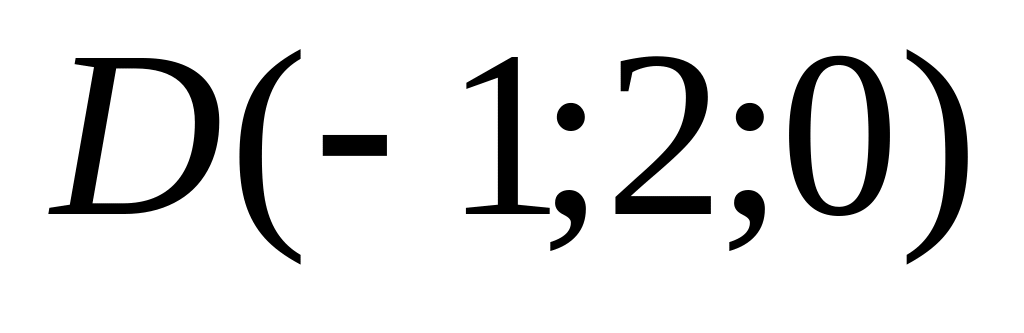
04)
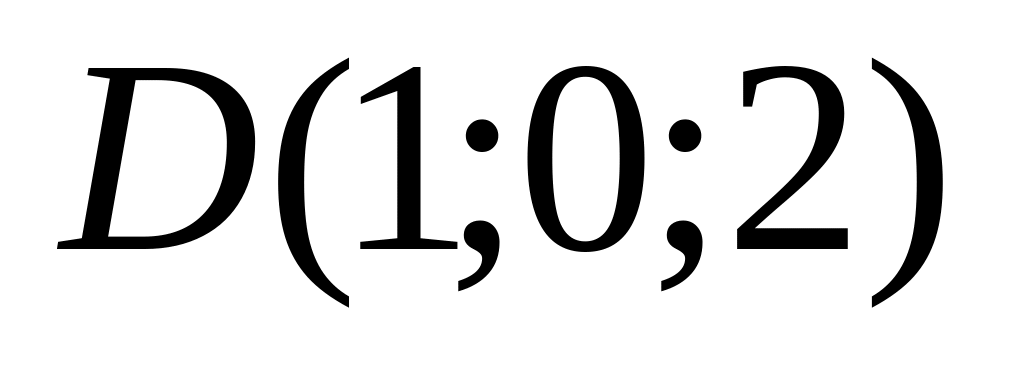
05)
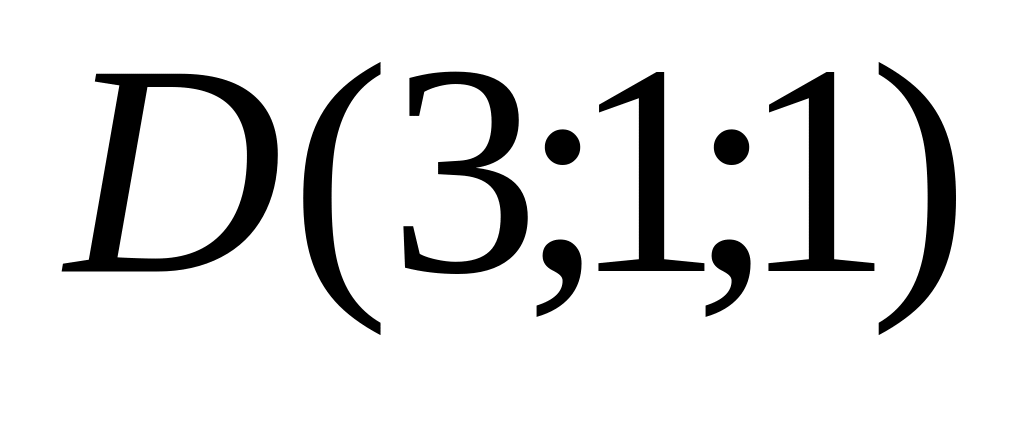
06)
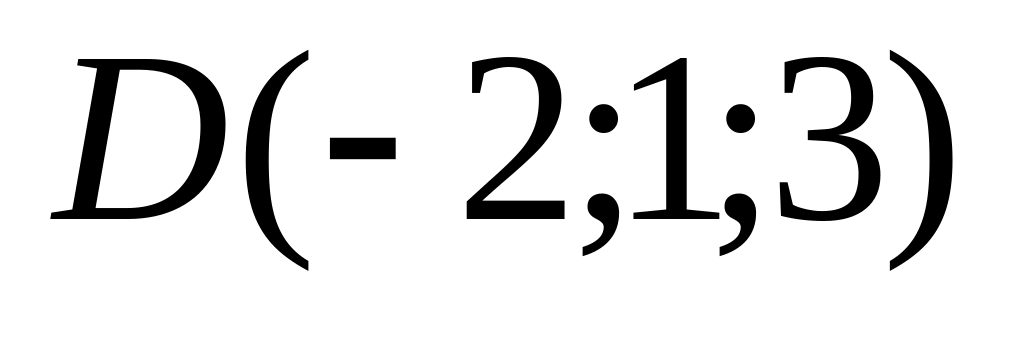
07)
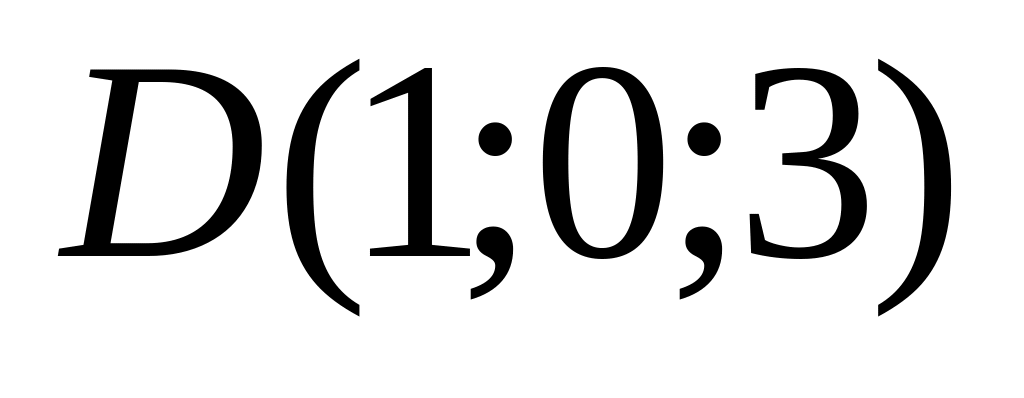
08)
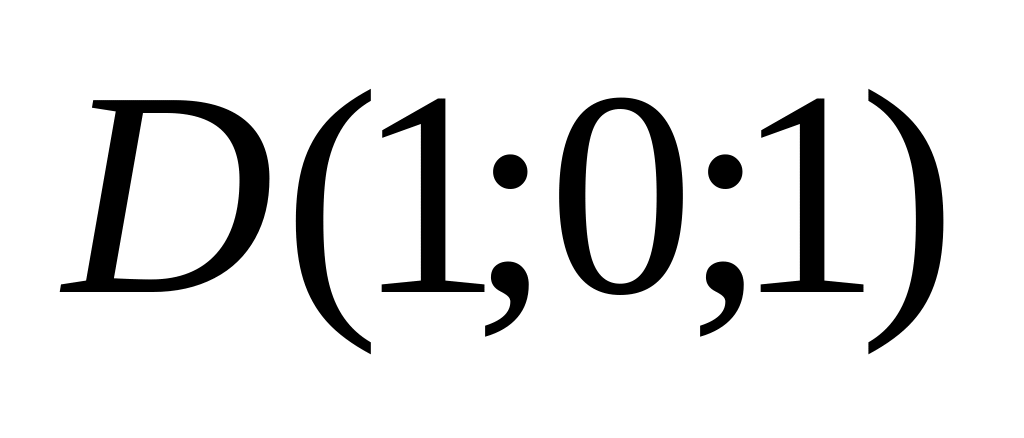
09)
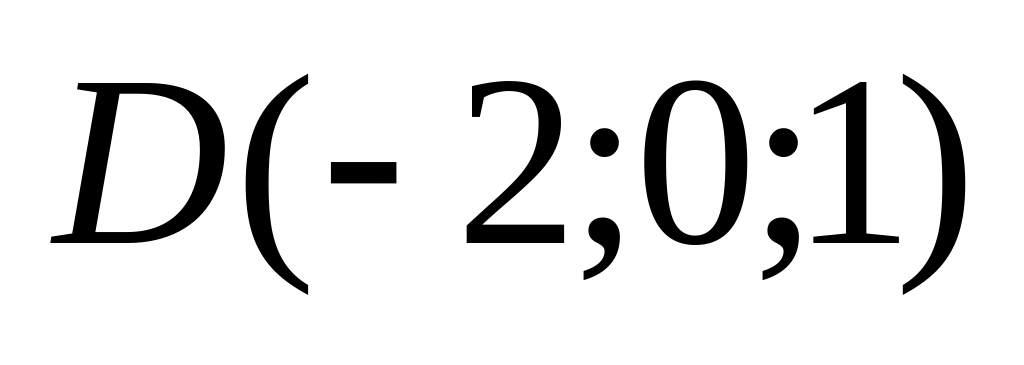
10)
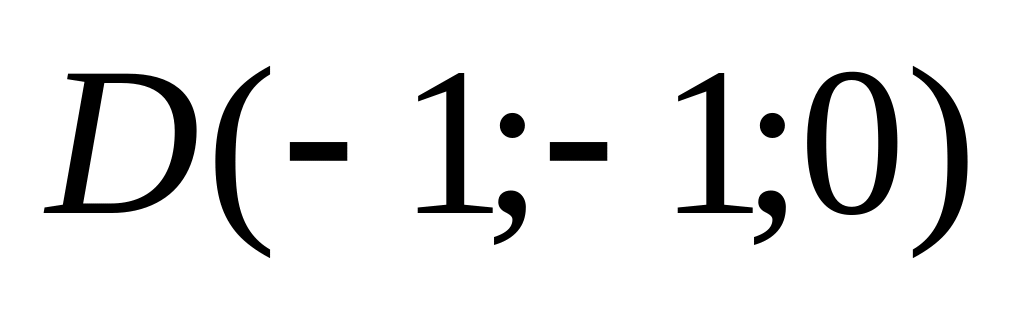
11)
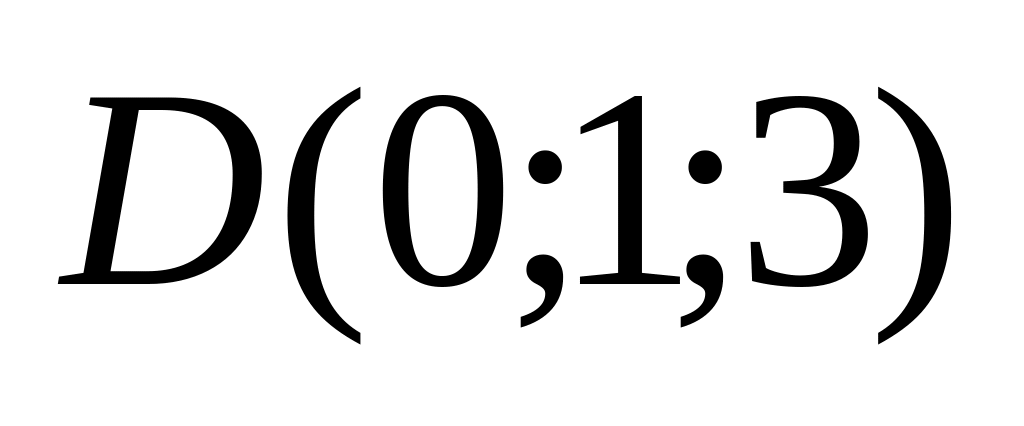
12)
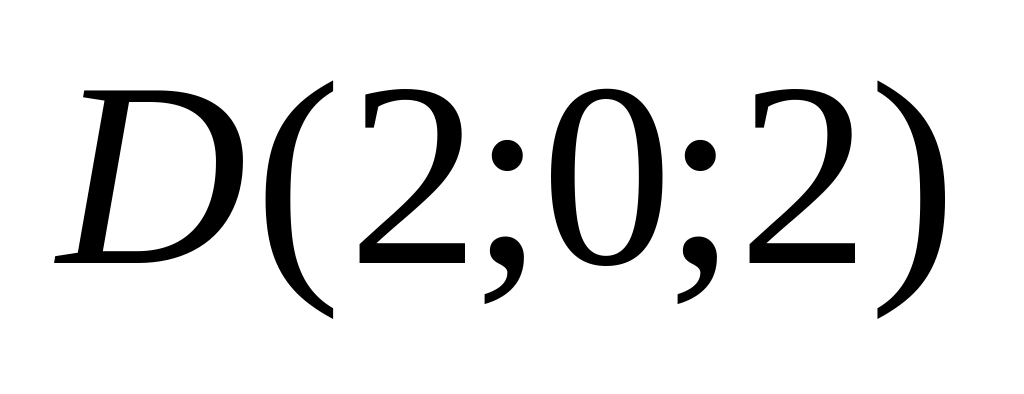
13)
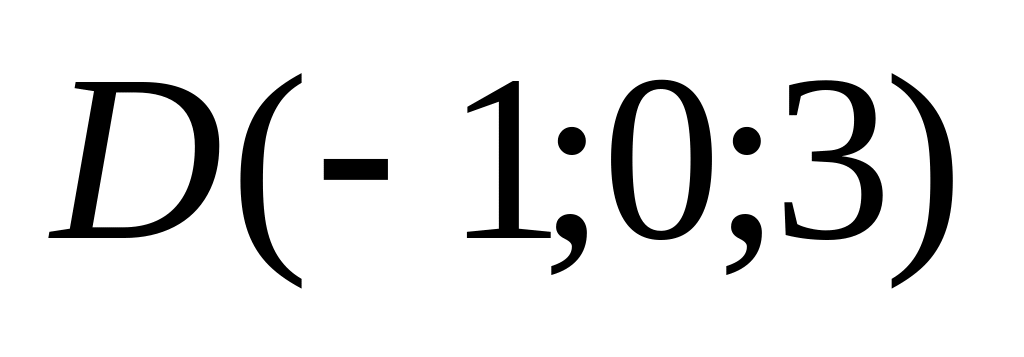
14)
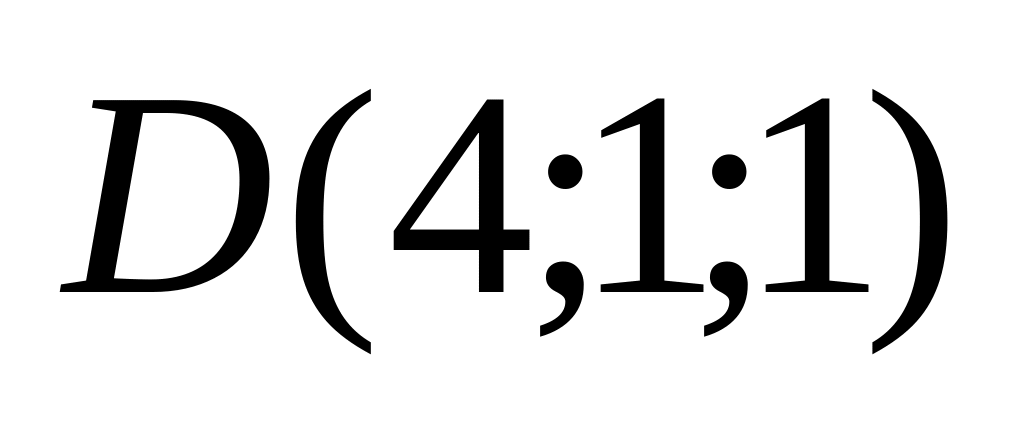
15)
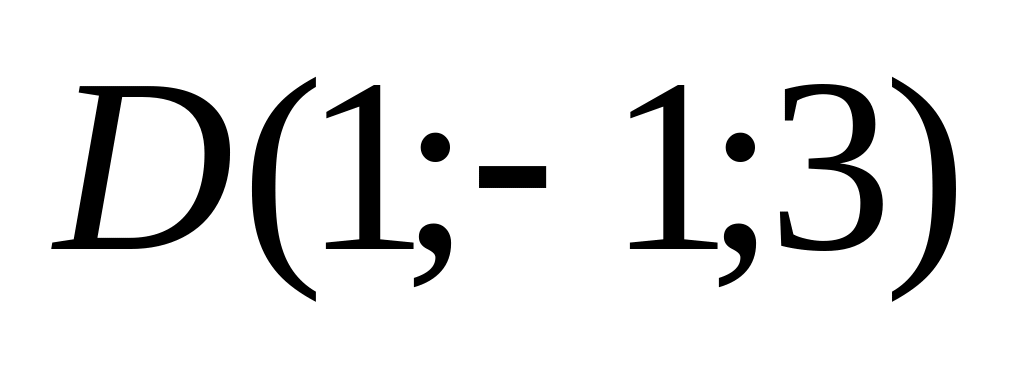
16)
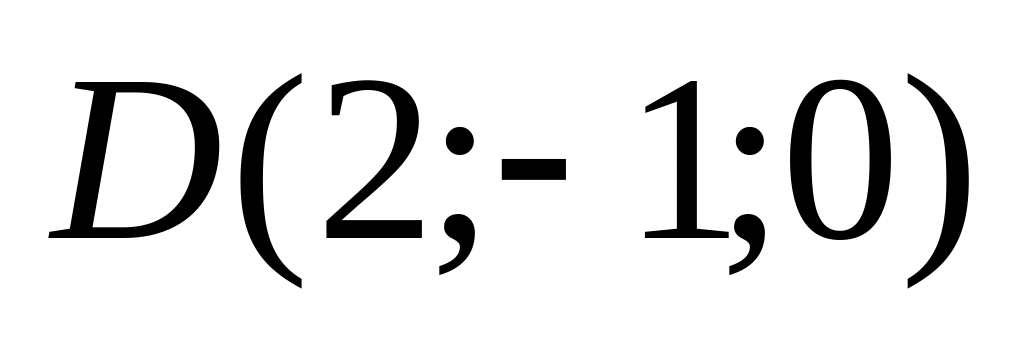
10. Треугольная пирамида задана своими вершинами . Найти:
а) площадь грани АВС;
б) объем пирамиды;
в) высоту пирамиды, опущенную из вершины на грань .
Варианты значений координат точек взять из заданий п. 8.
-
01)
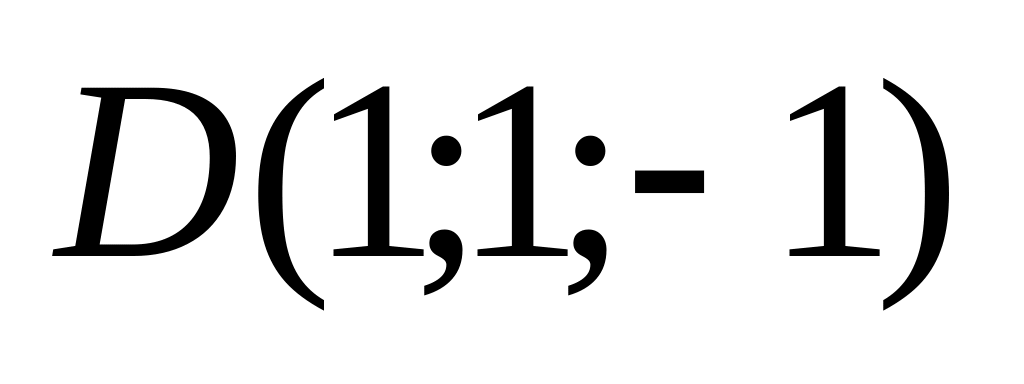
02)
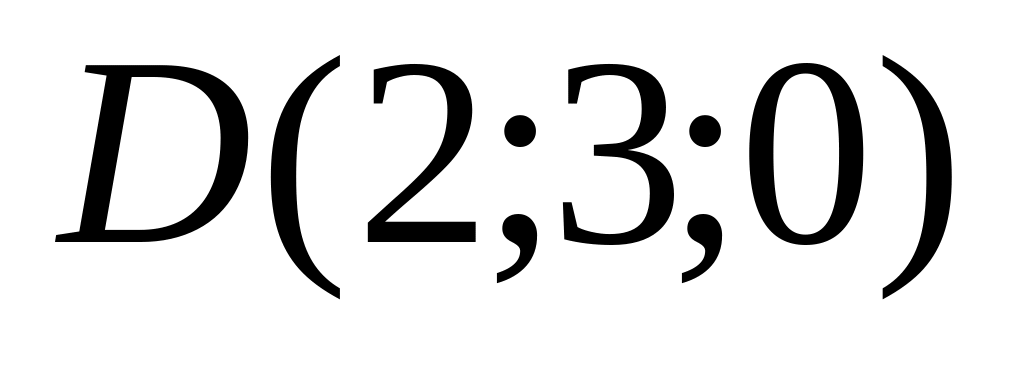
03)
04)
05)
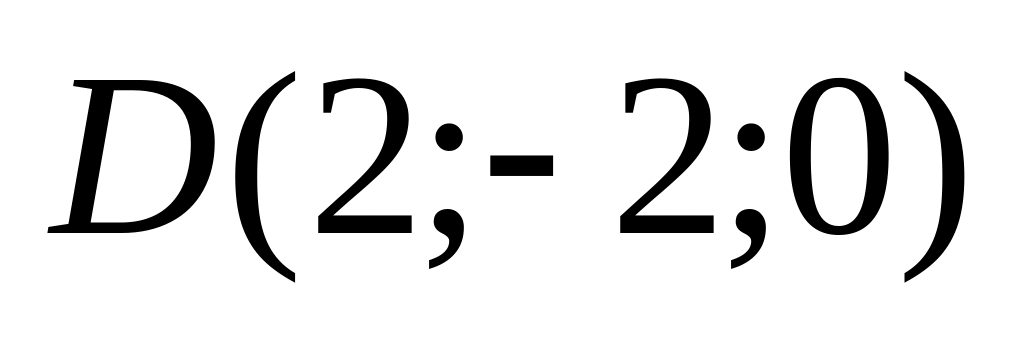
06)
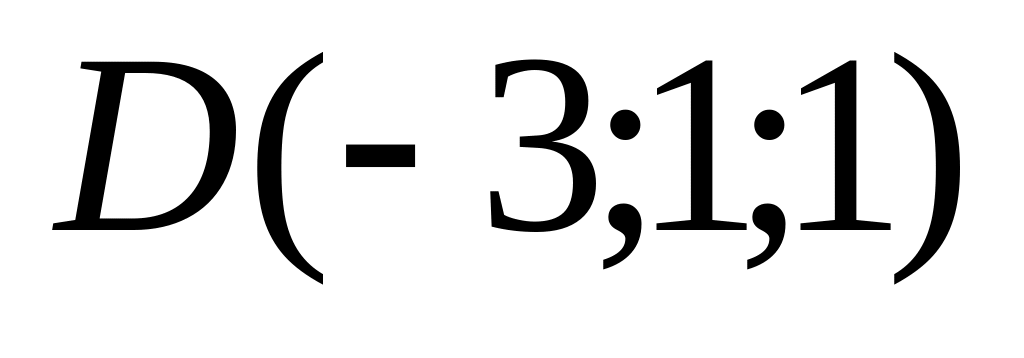
07)
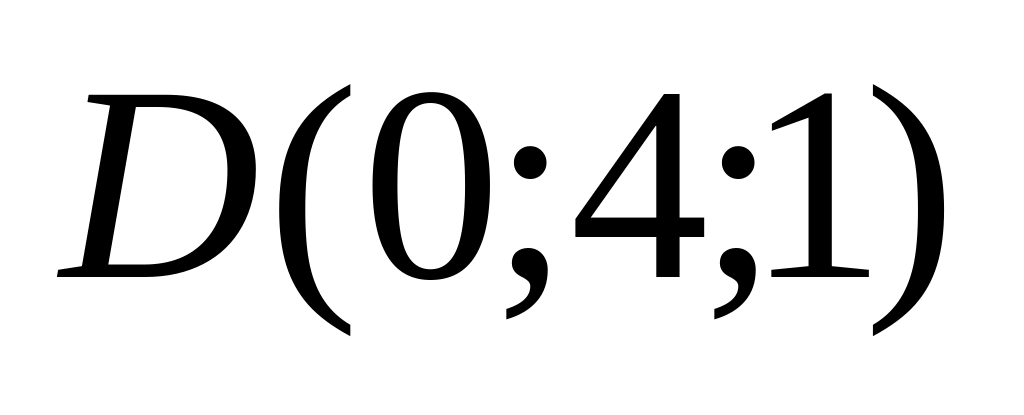
08)
09)
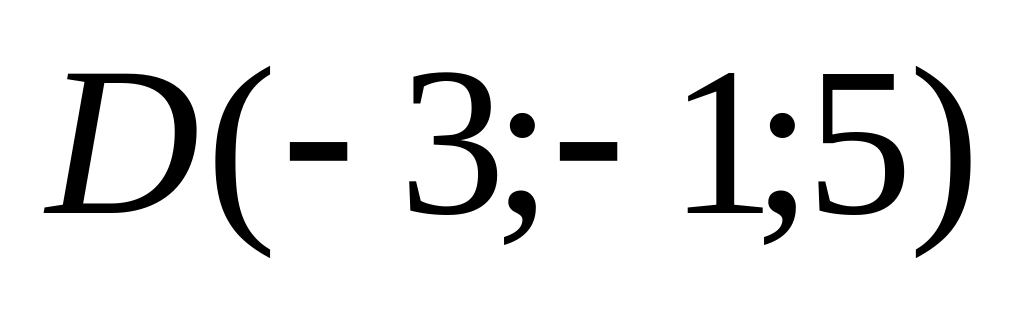
10)
11)
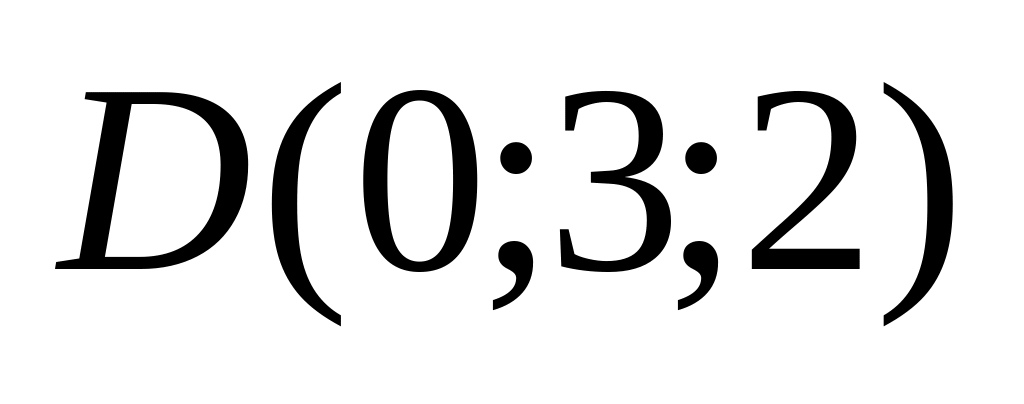
12)
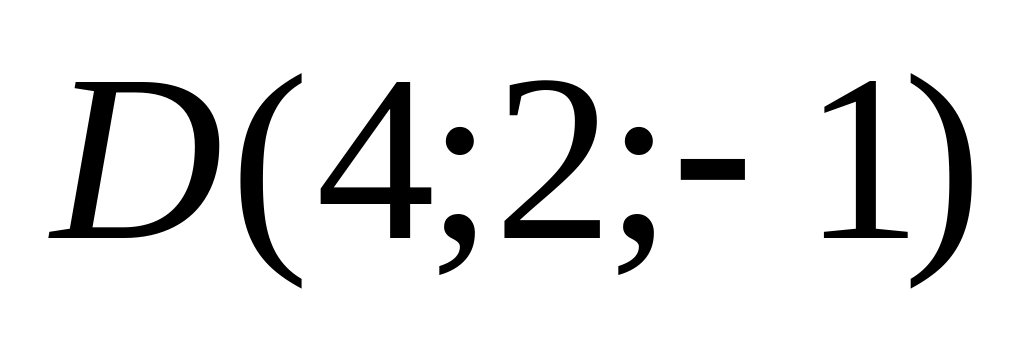
13)
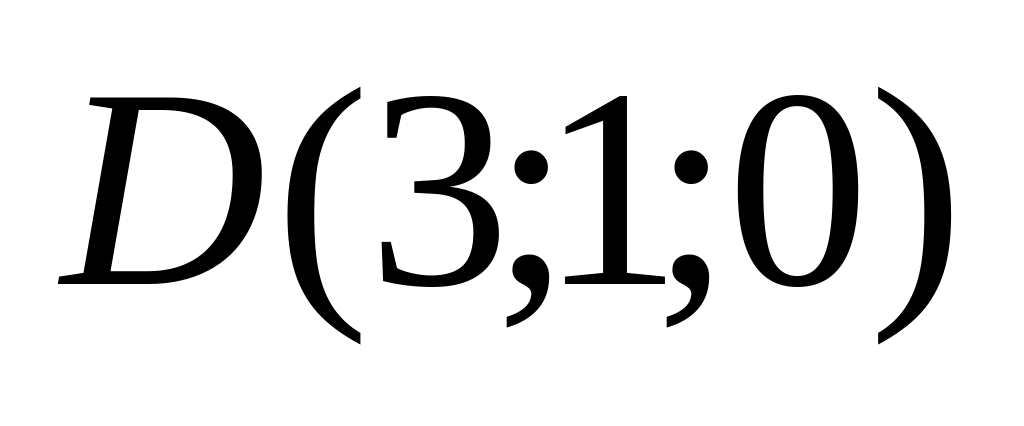
14)
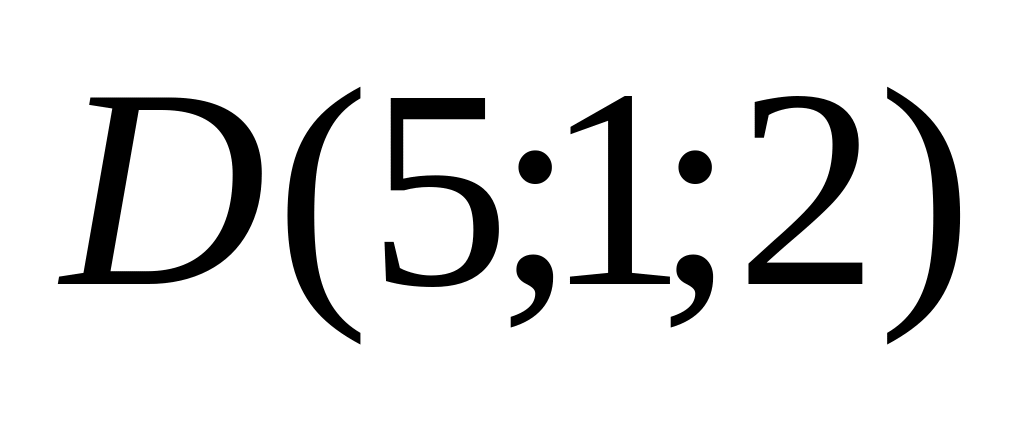
15)
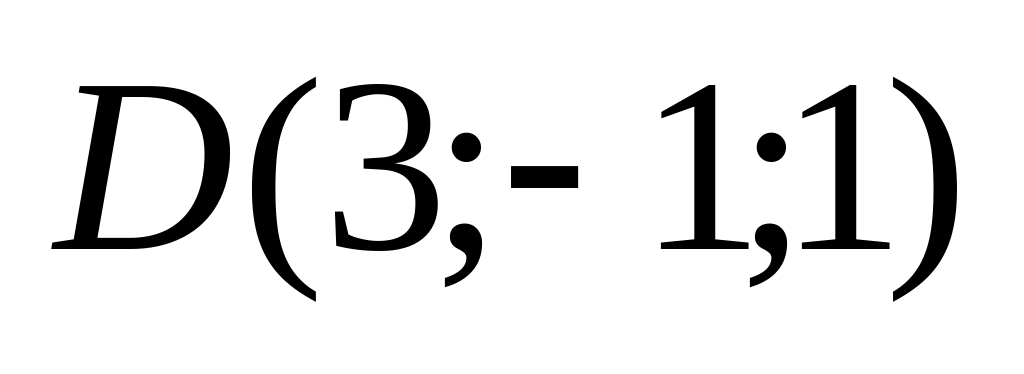
16)
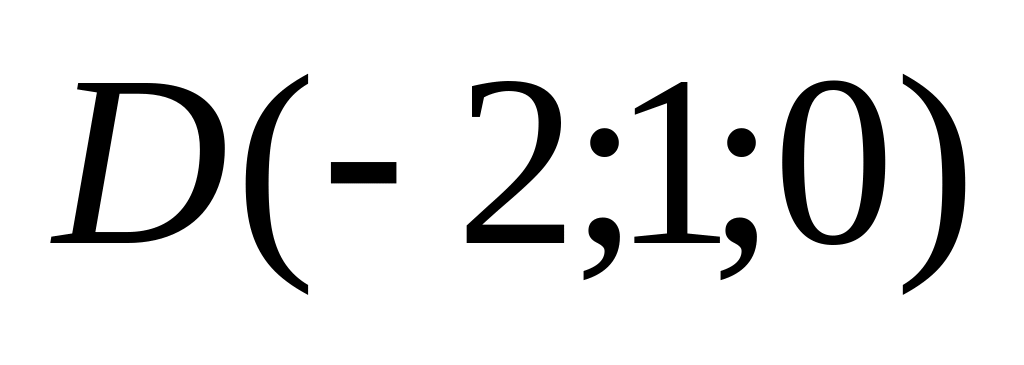
11. Найти
,
и угол
между
и
,
если заданы разложения
и
по векторам
и
,
а также заданы
,
и угол
между
и
.
-
01)
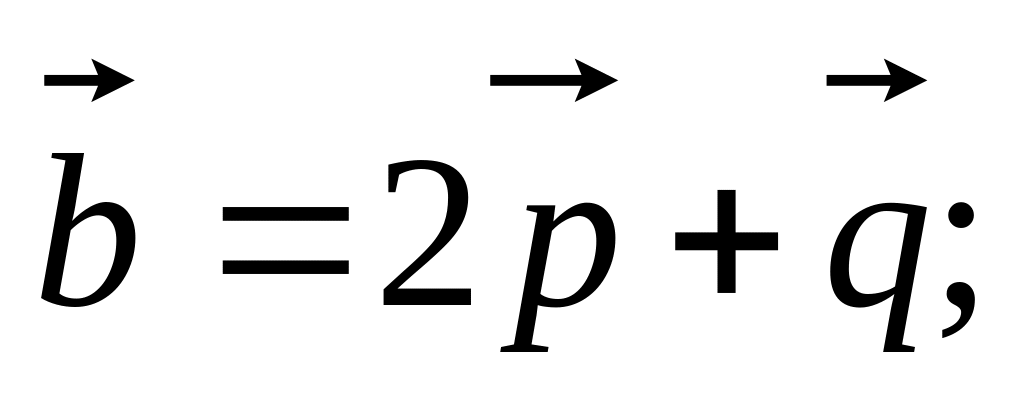
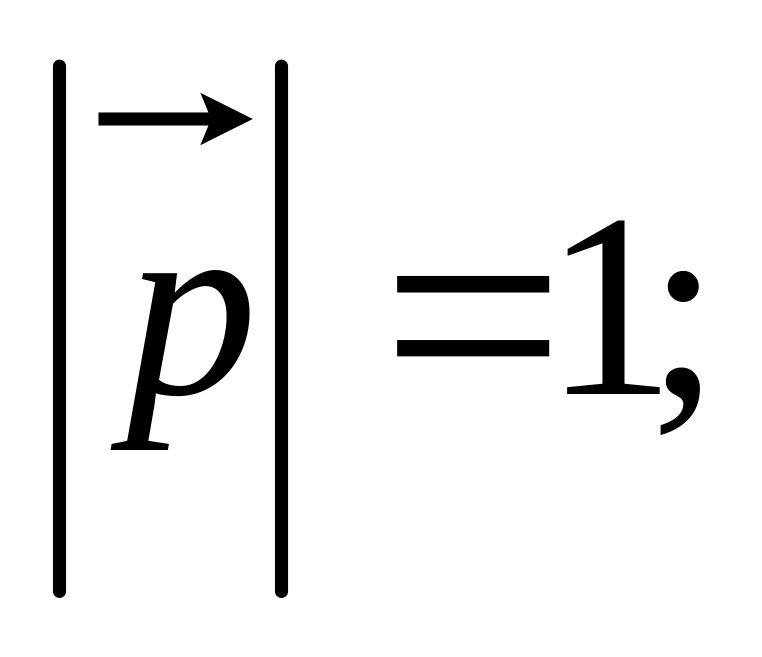
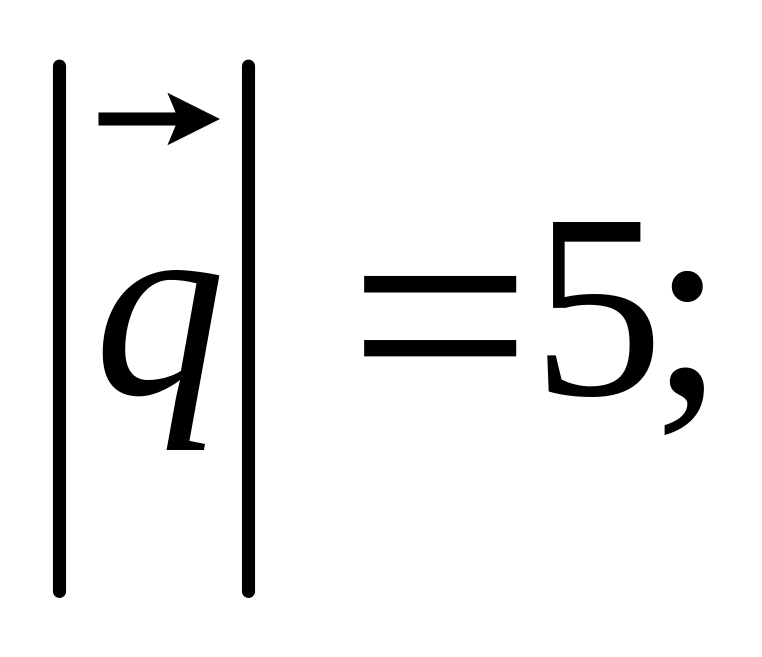
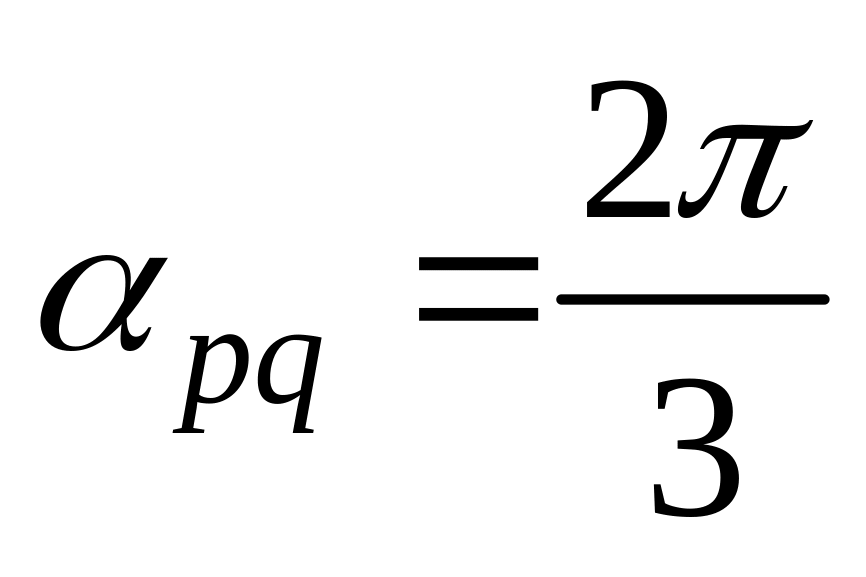
02)
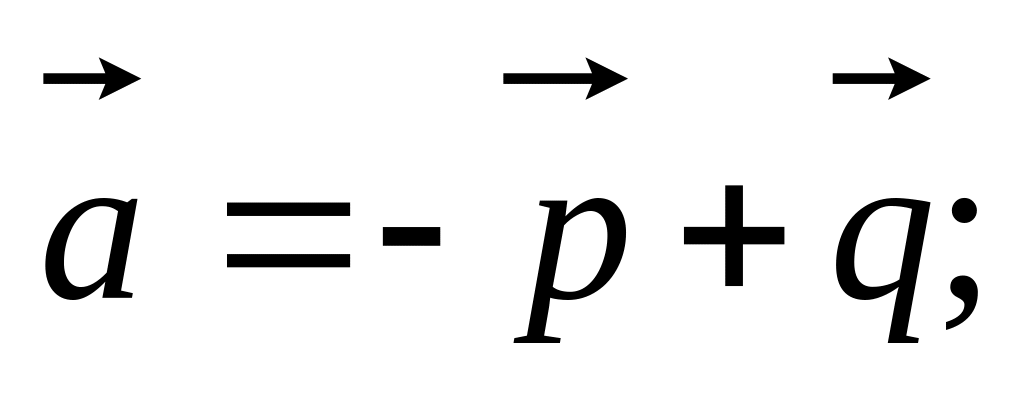
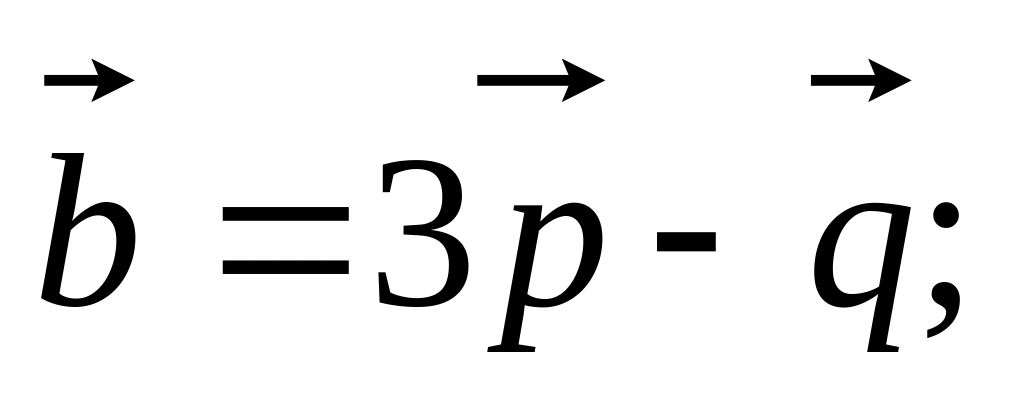
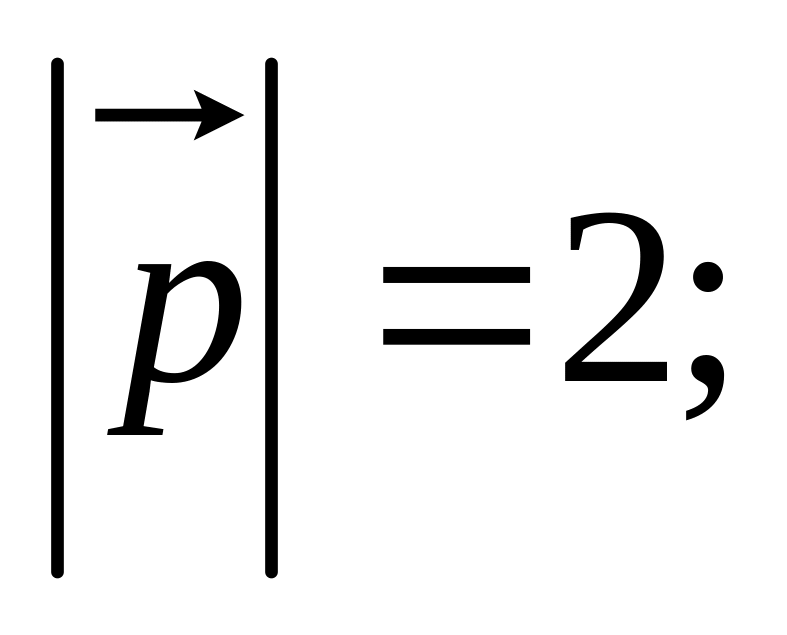
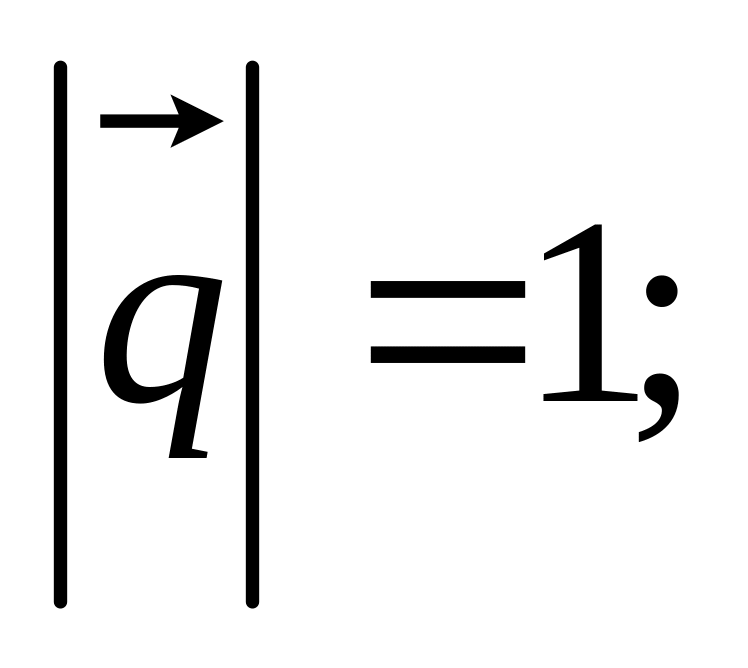
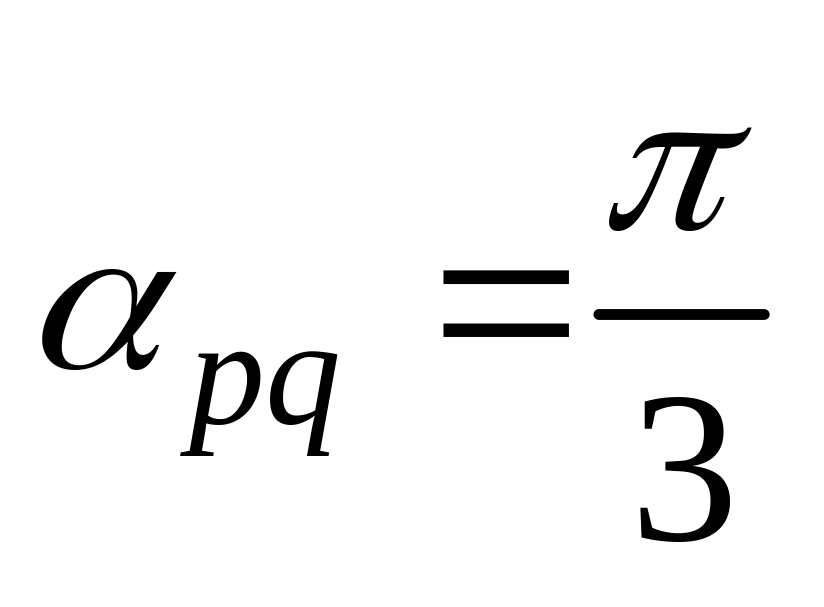
03)
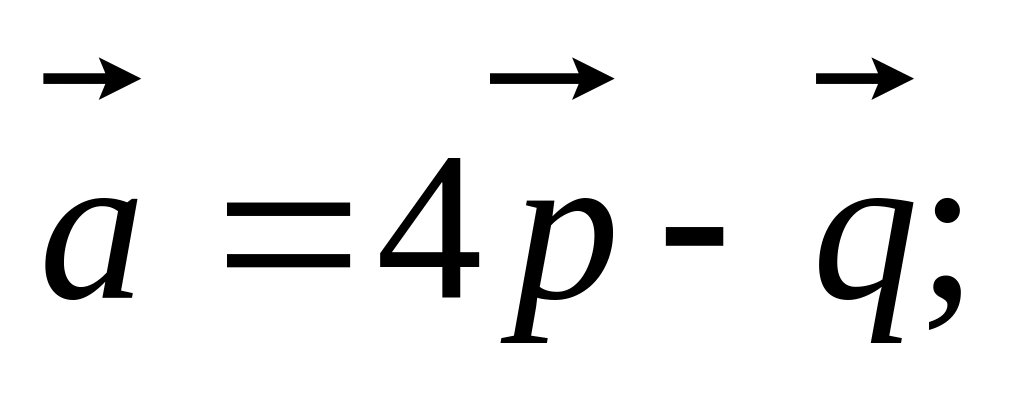
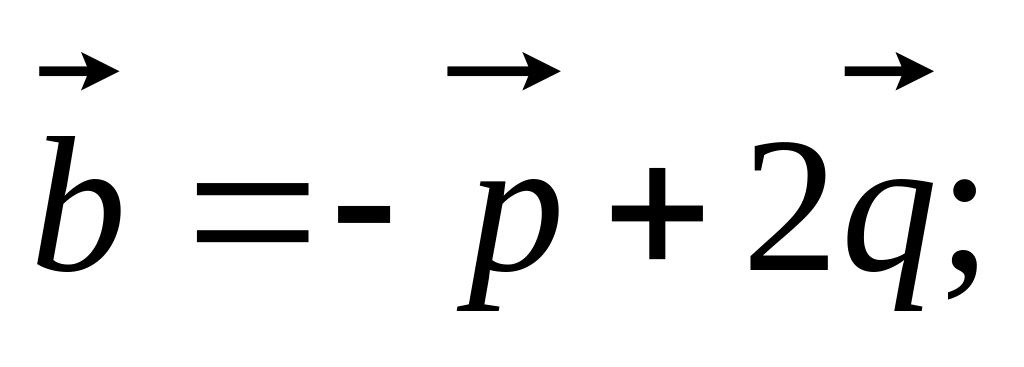
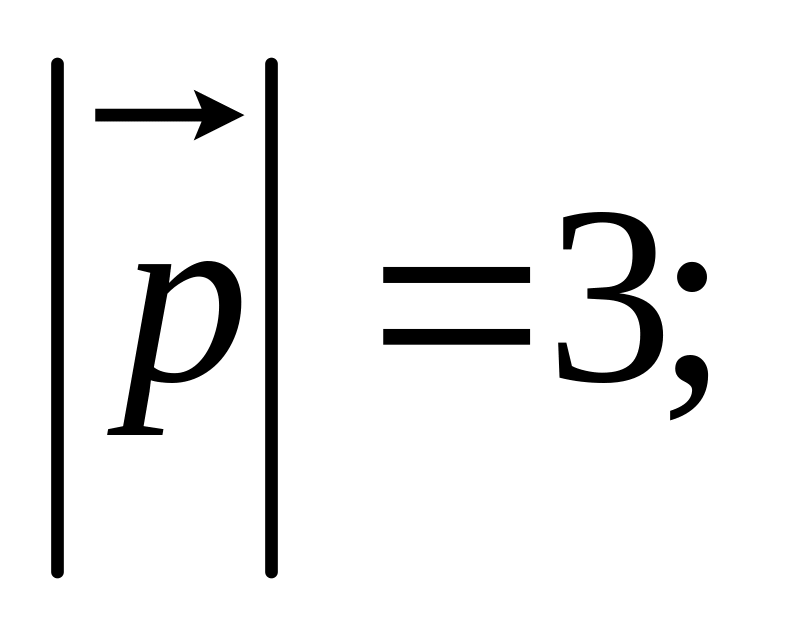
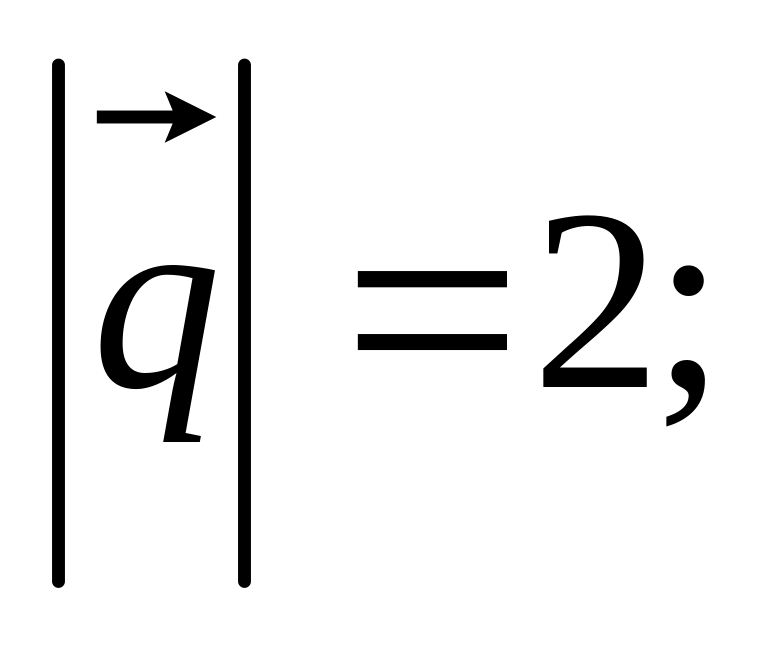
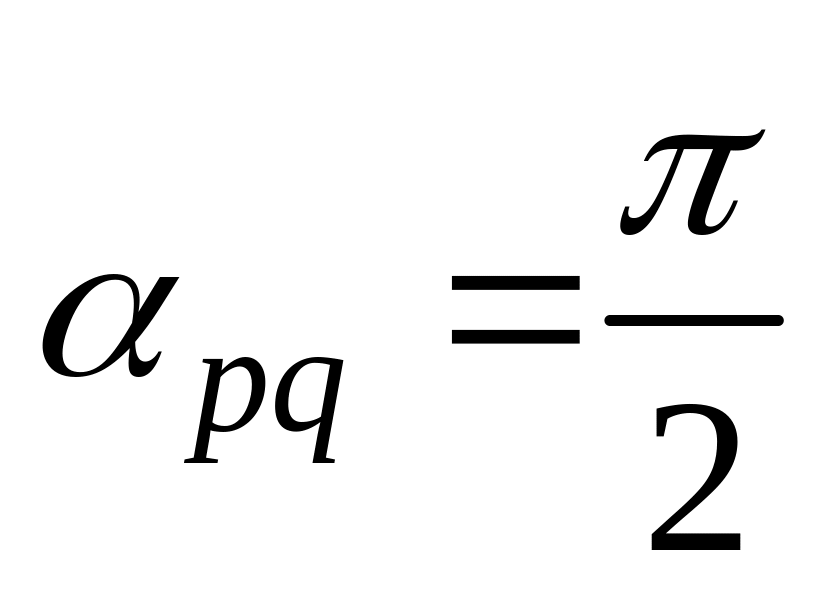
04)
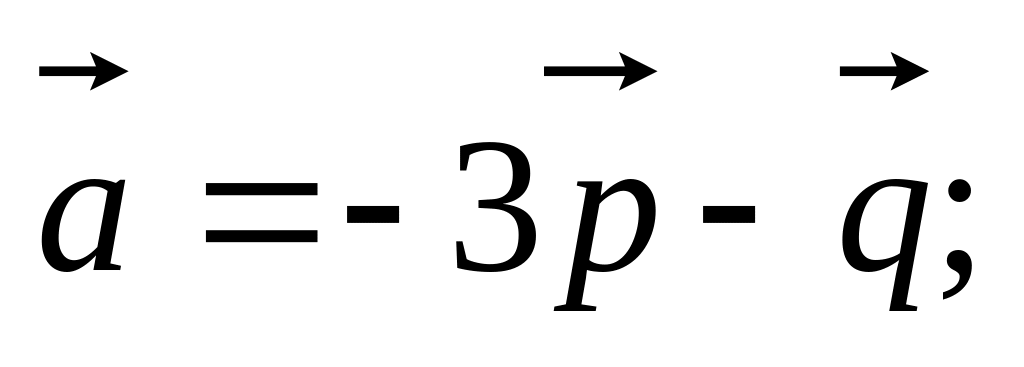
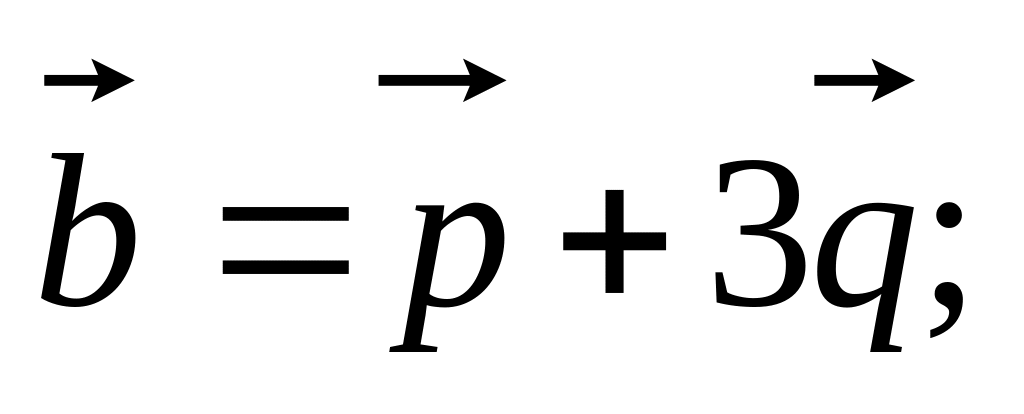
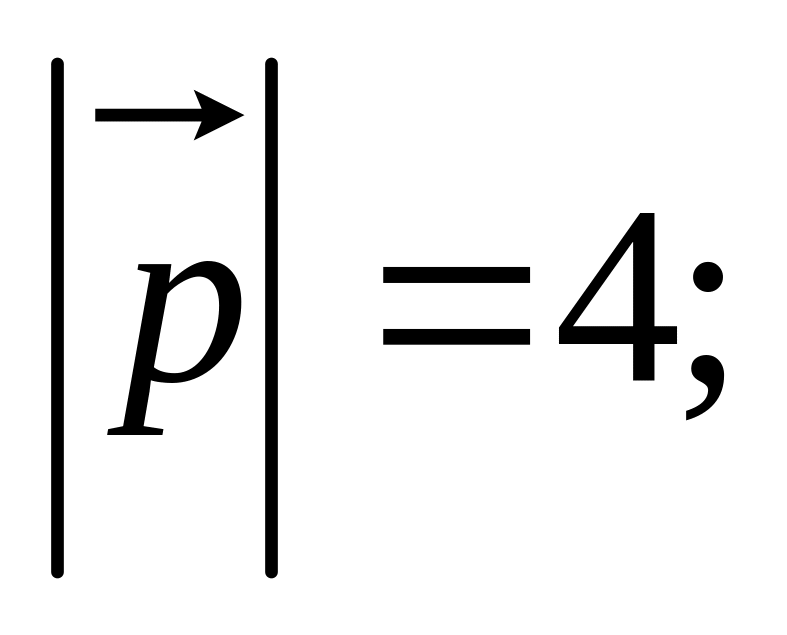
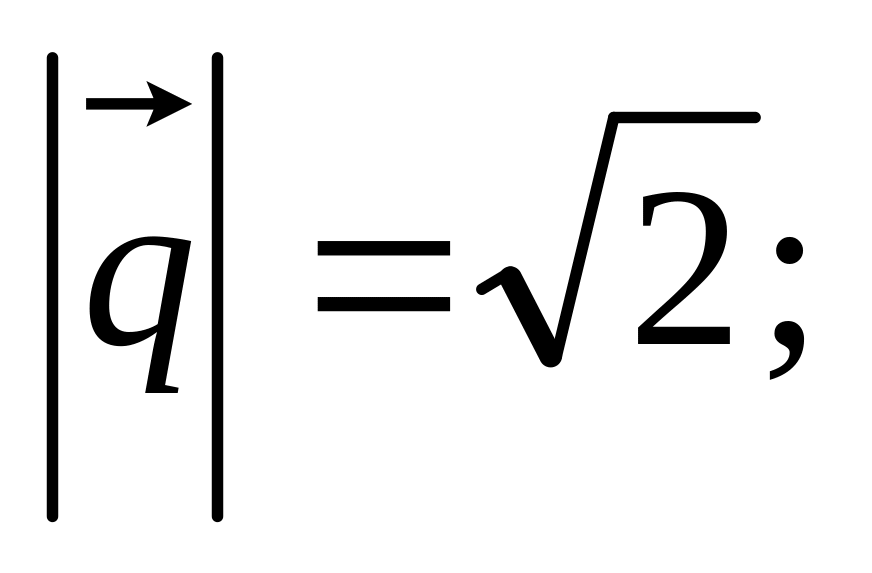
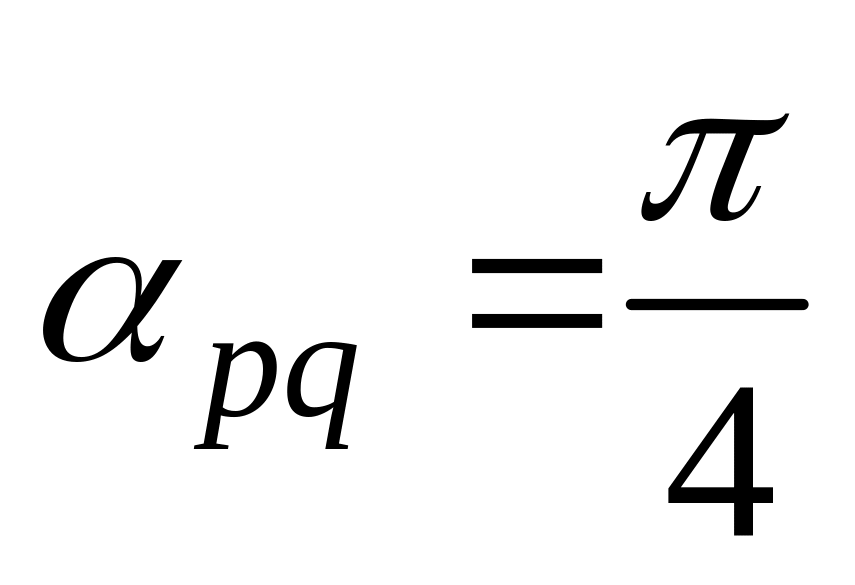
05)
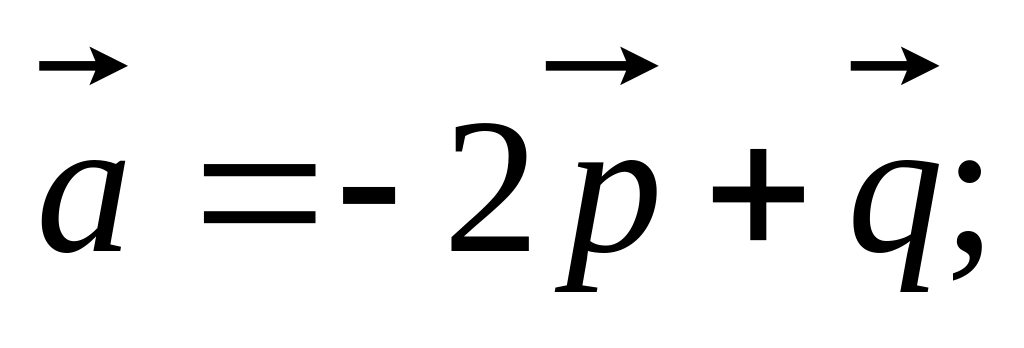
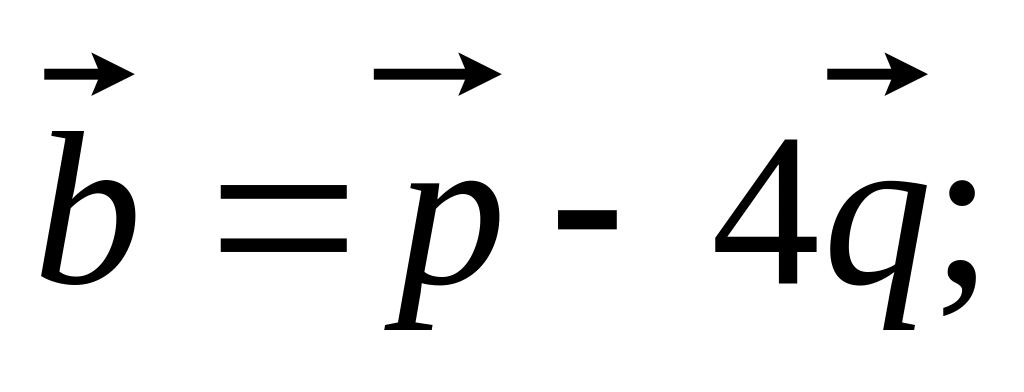
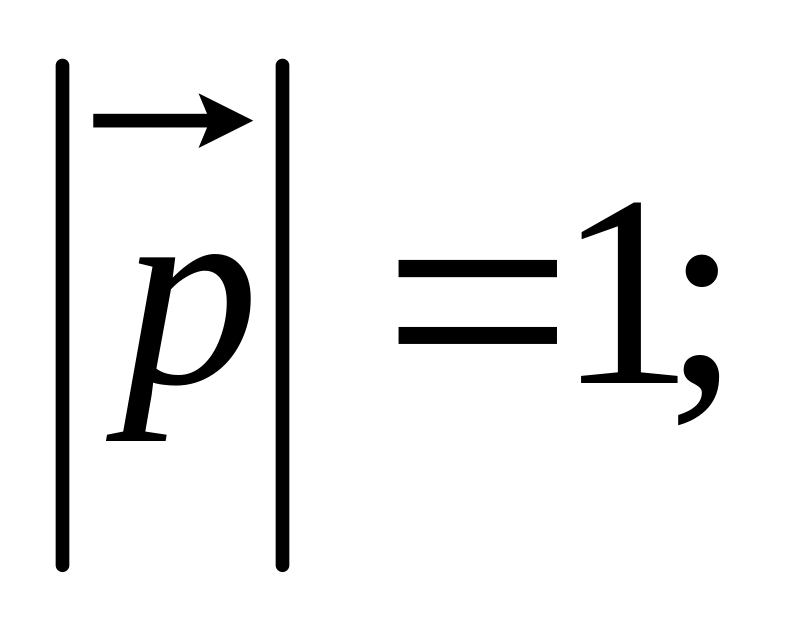
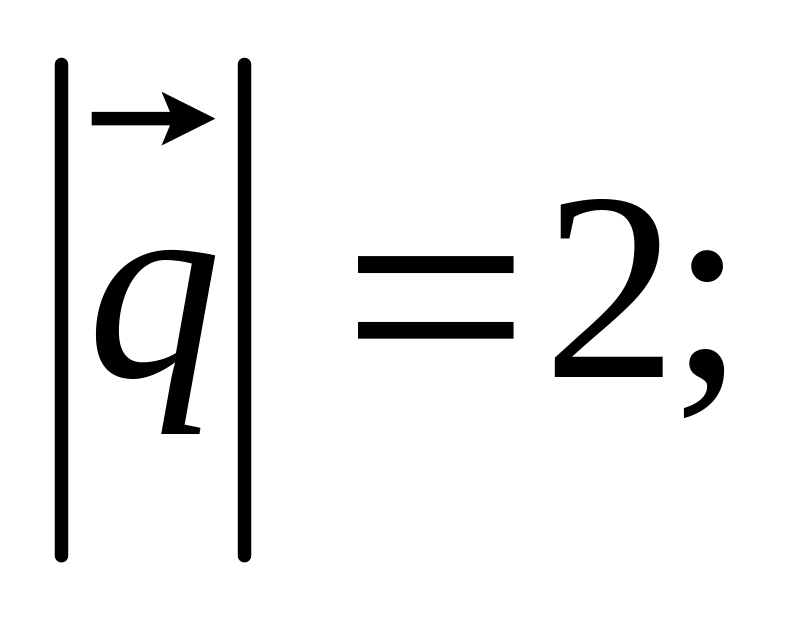
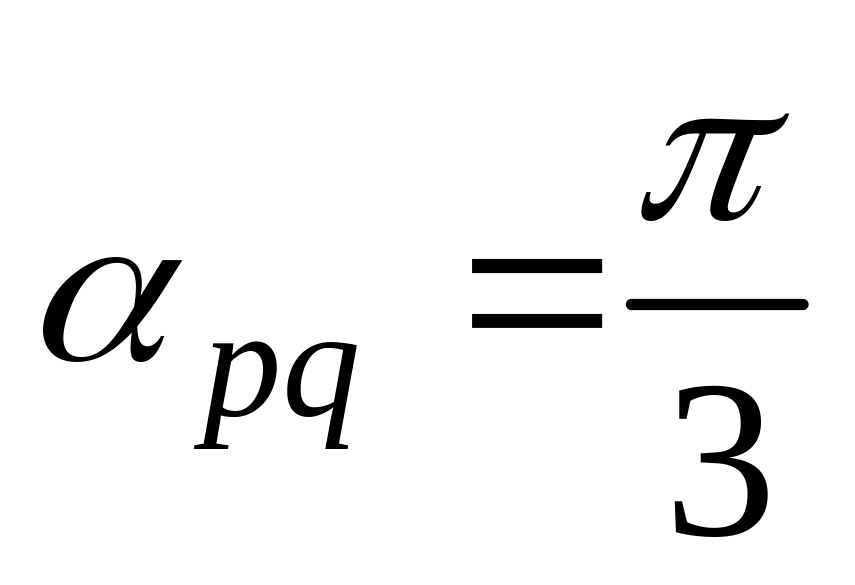
06)
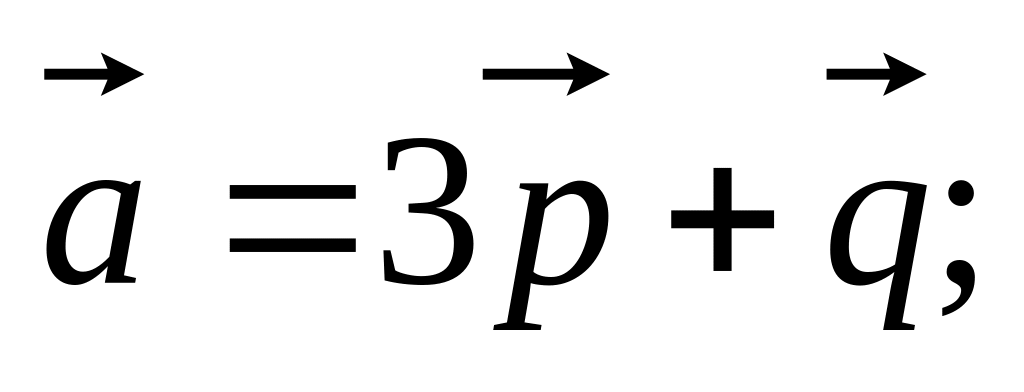
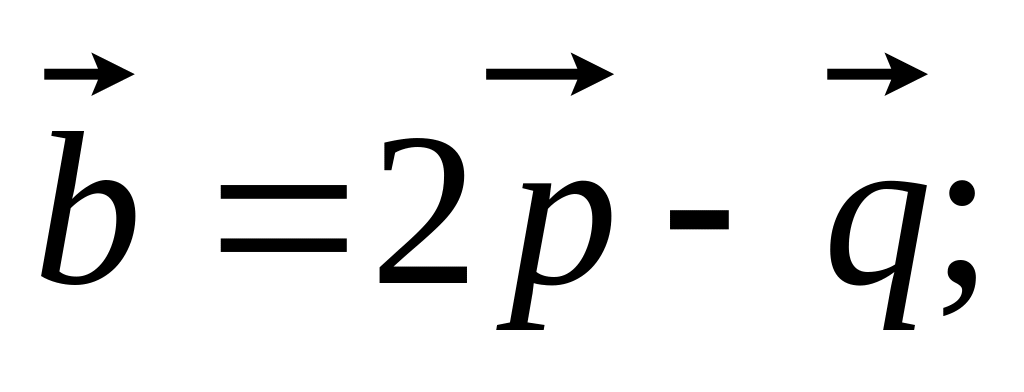
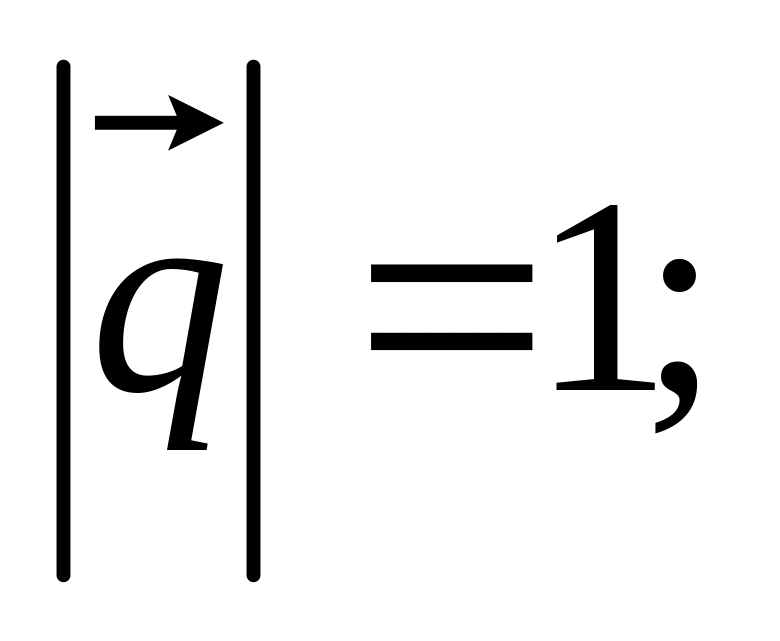
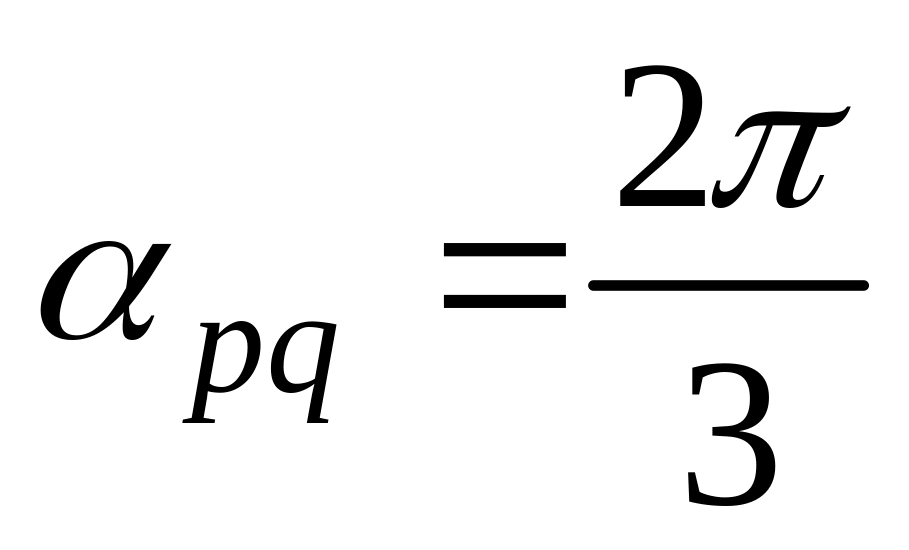
07)
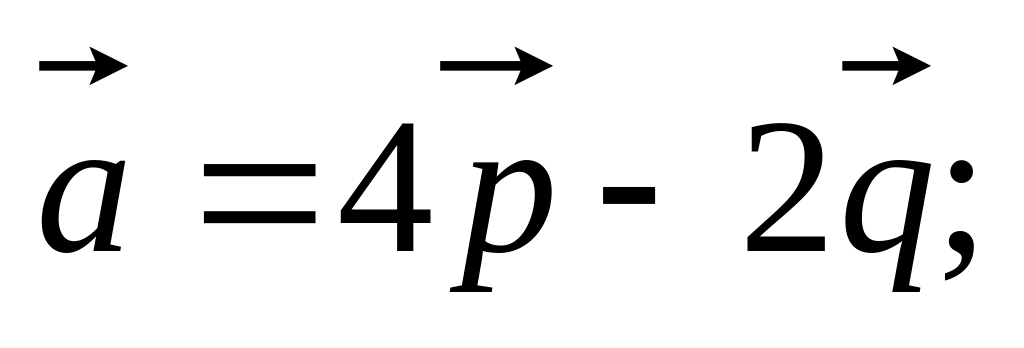
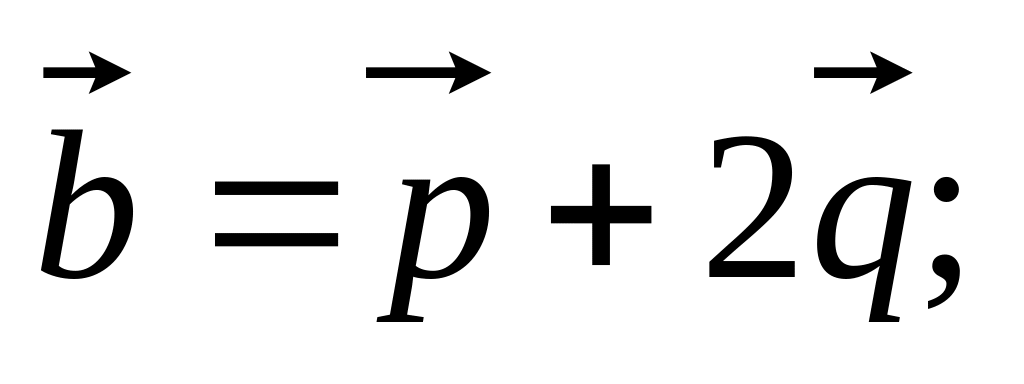
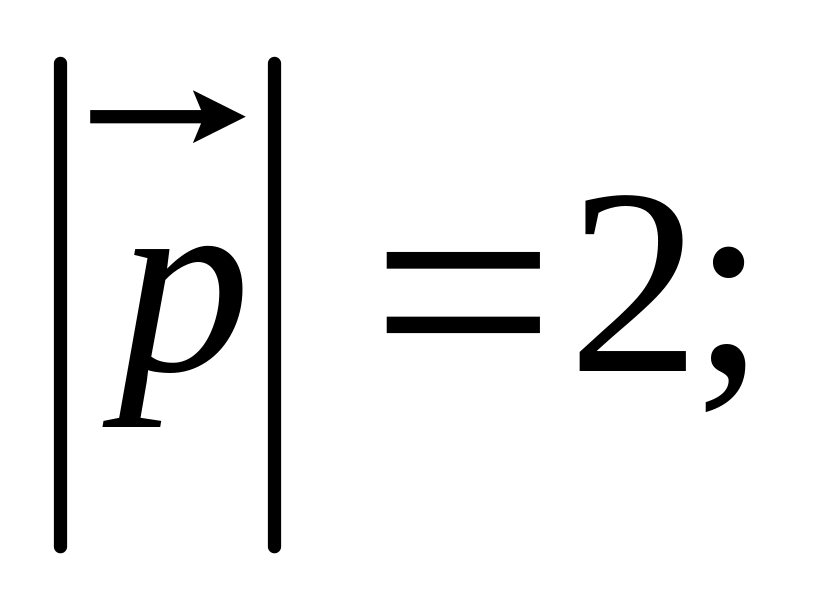
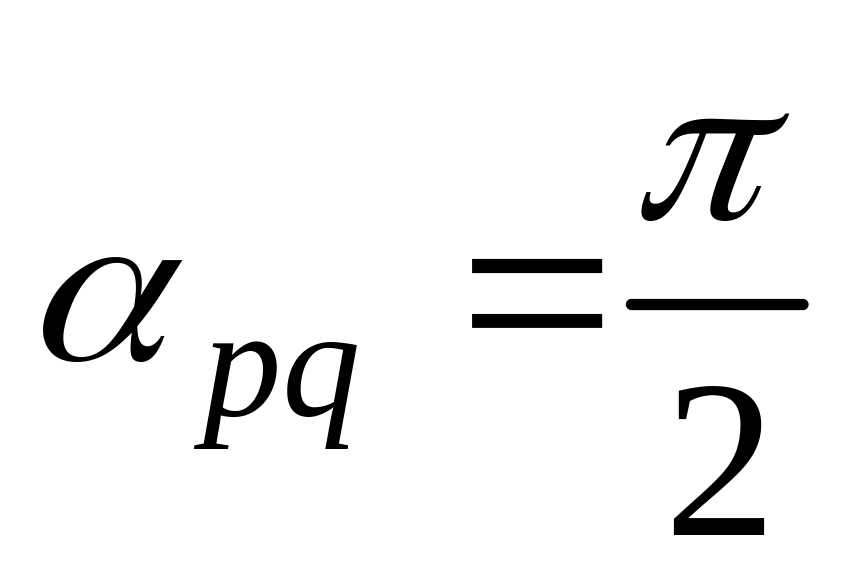
08)
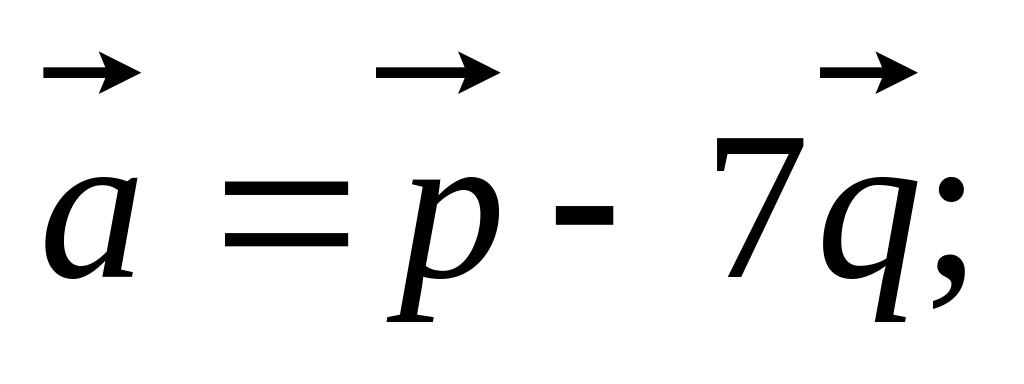
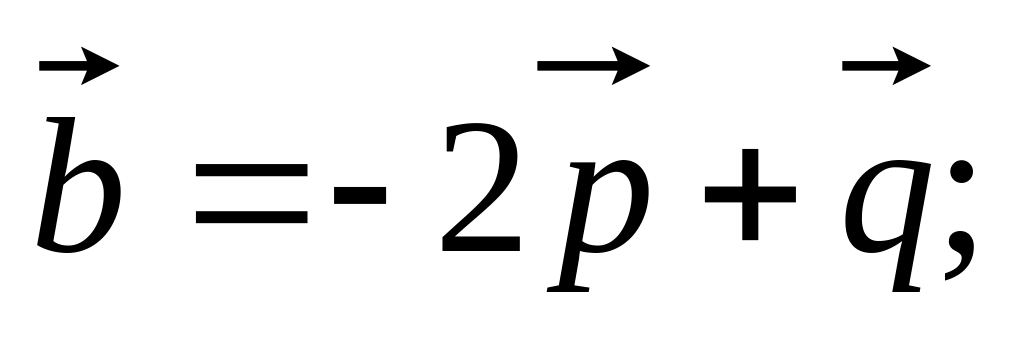
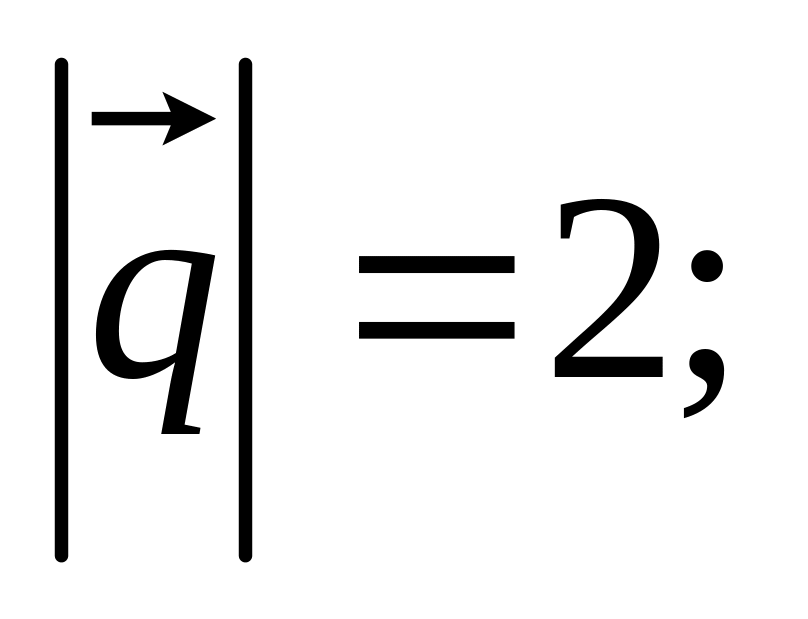
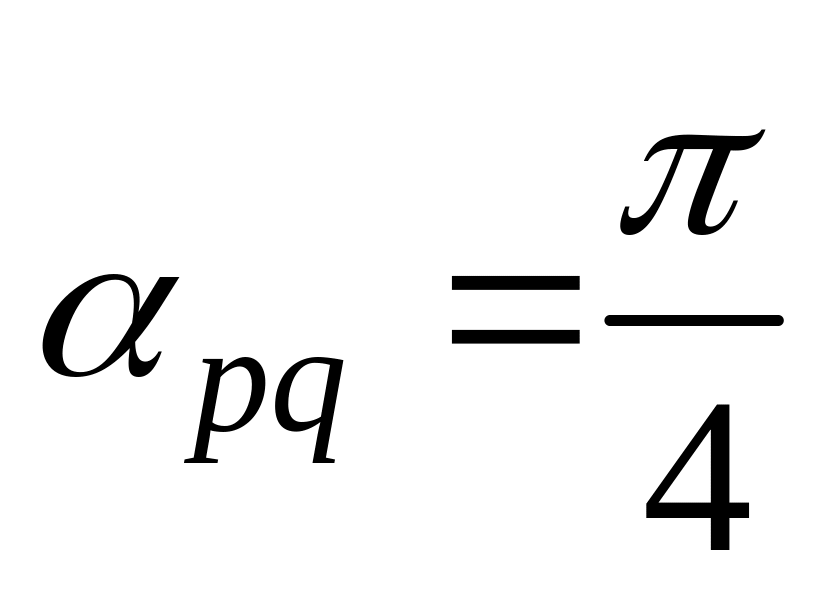
09)
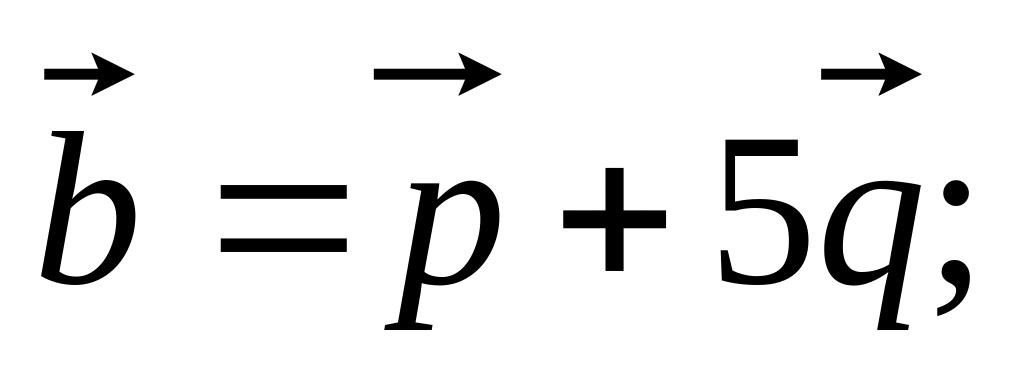
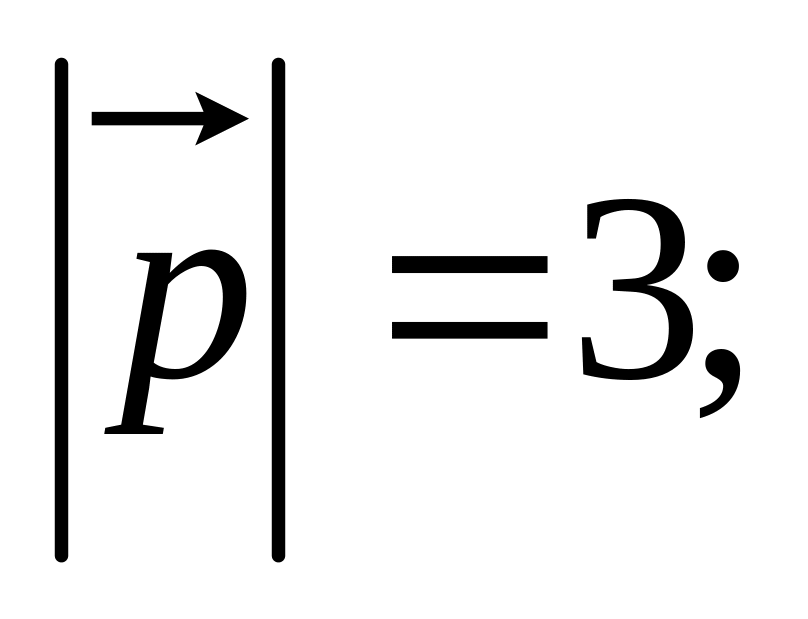
10)
;
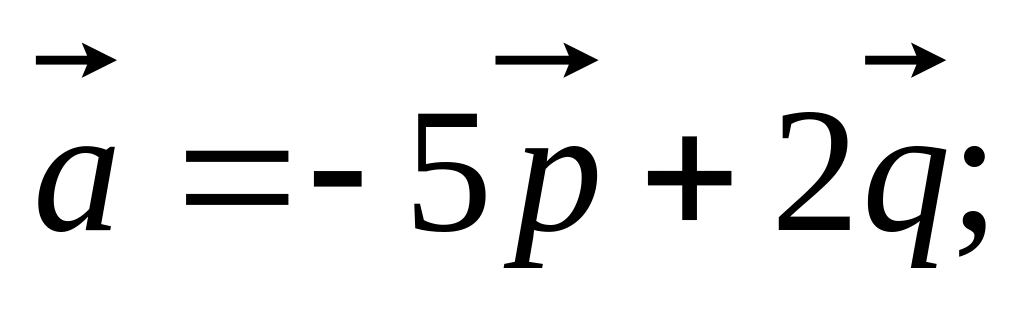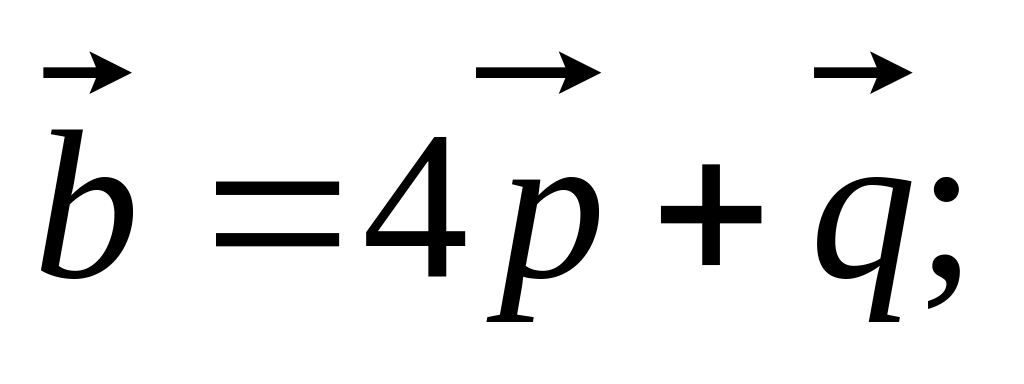
11)
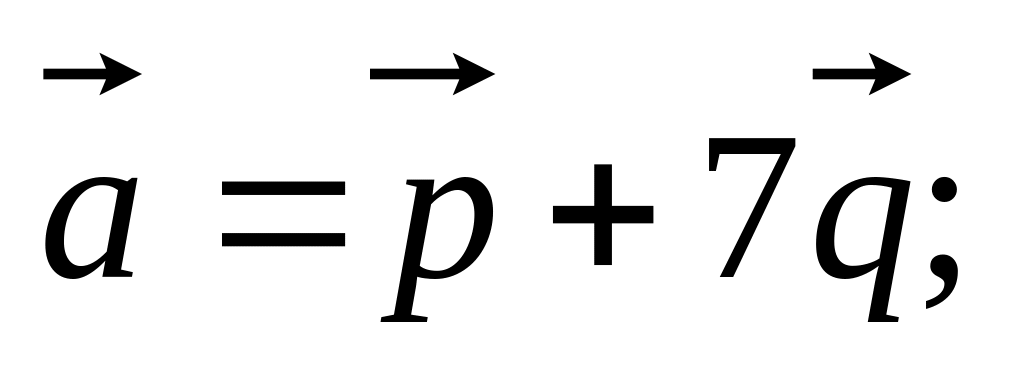
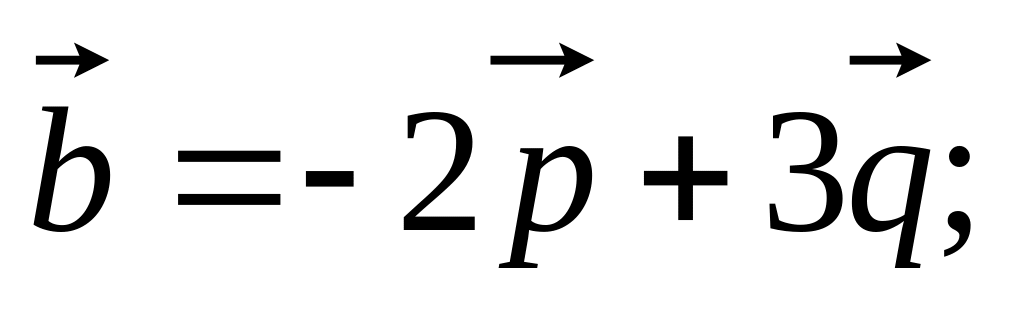
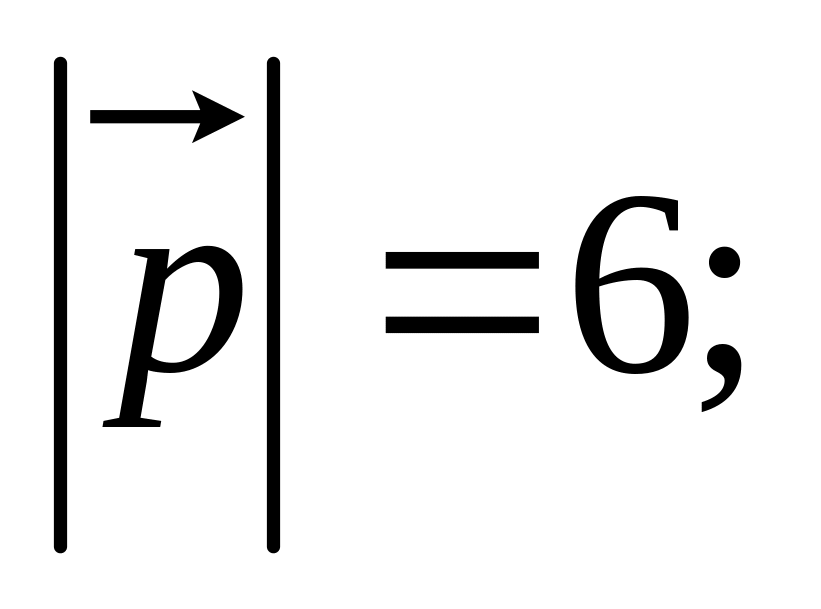
12)
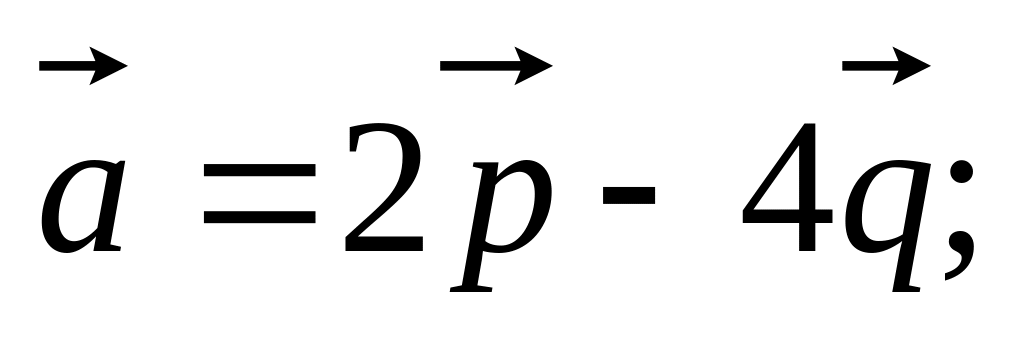
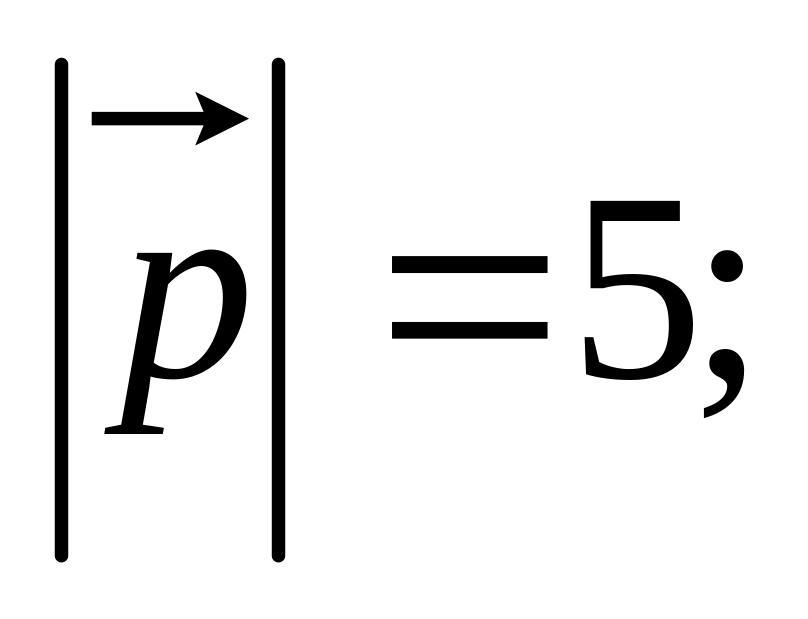
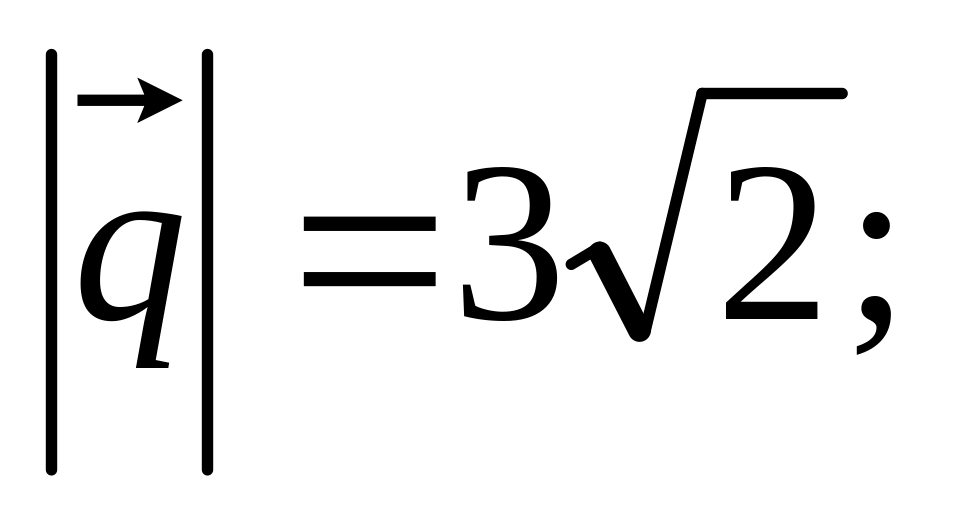
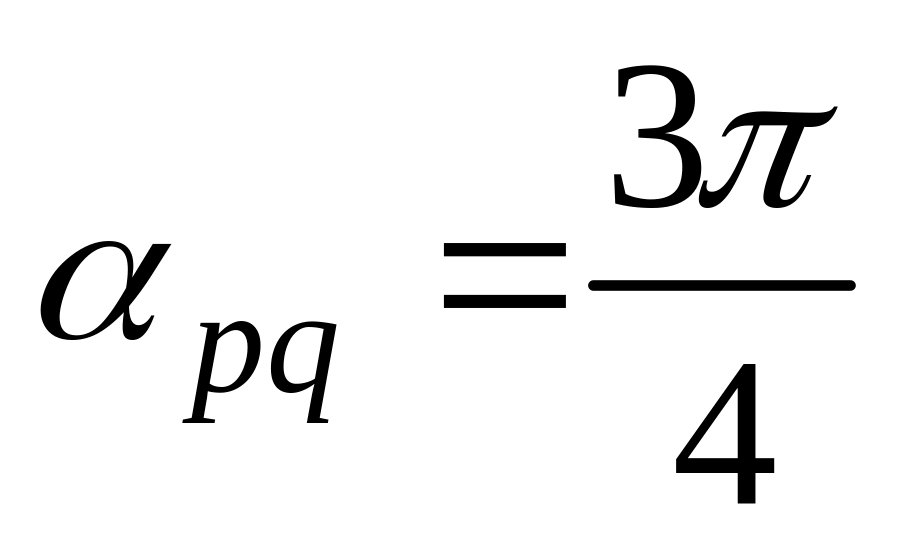
13)
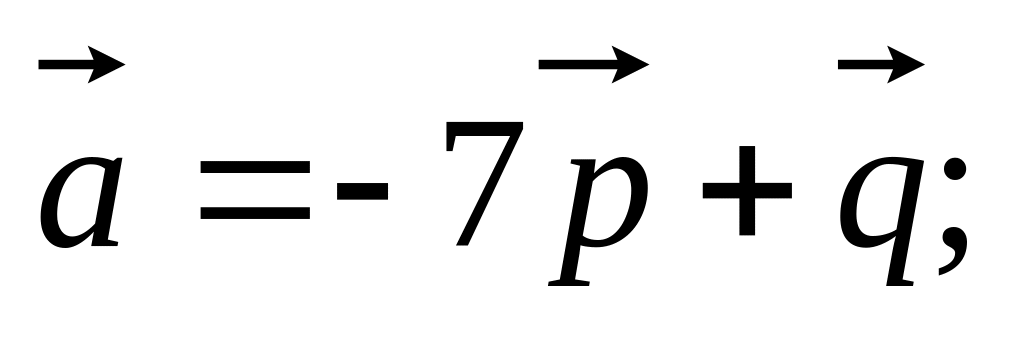
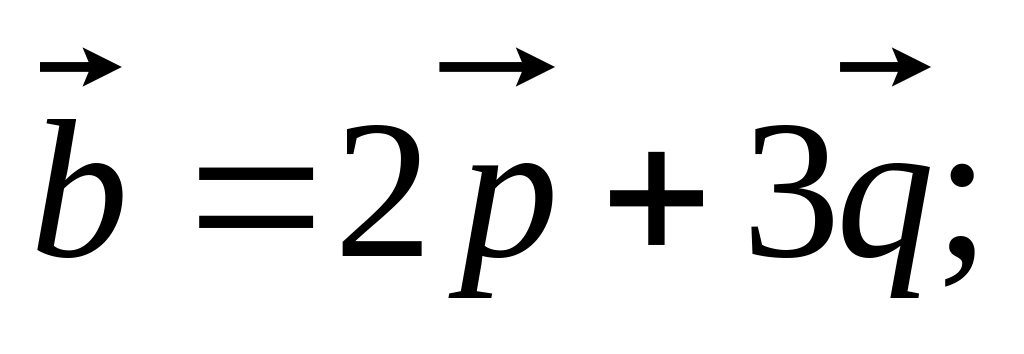
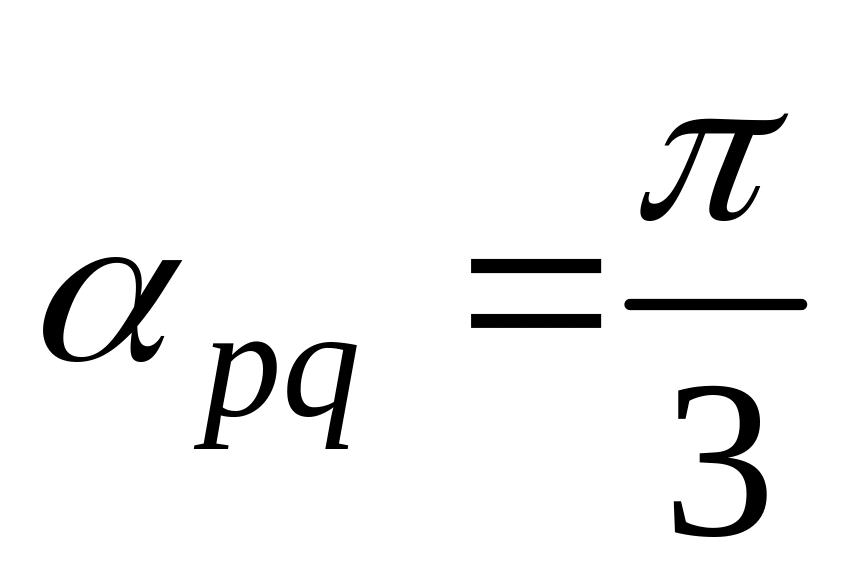
14)
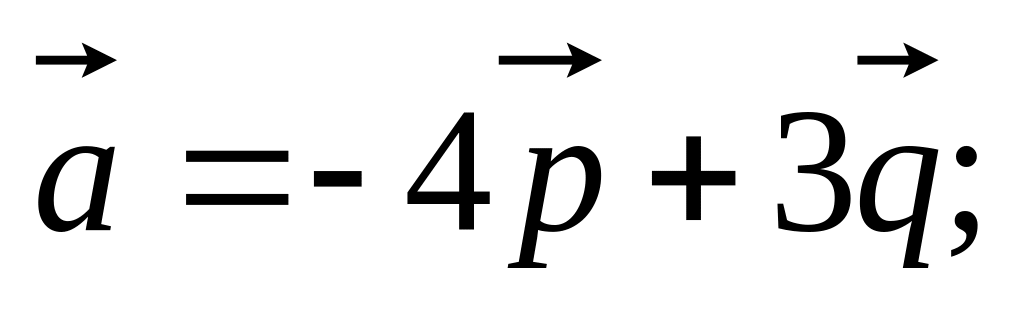
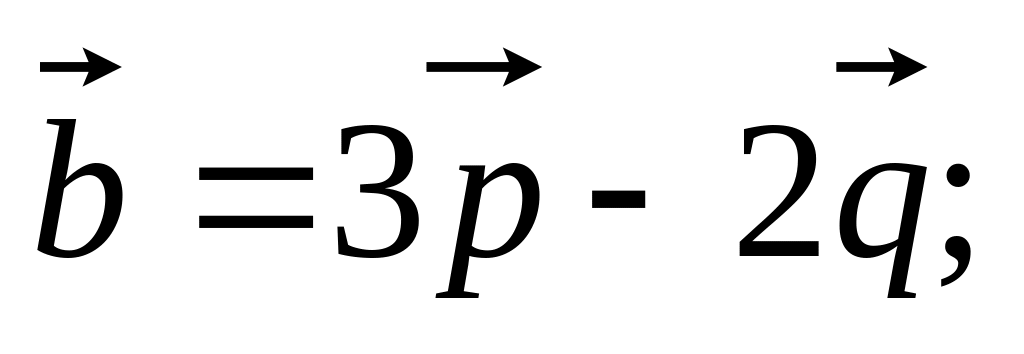
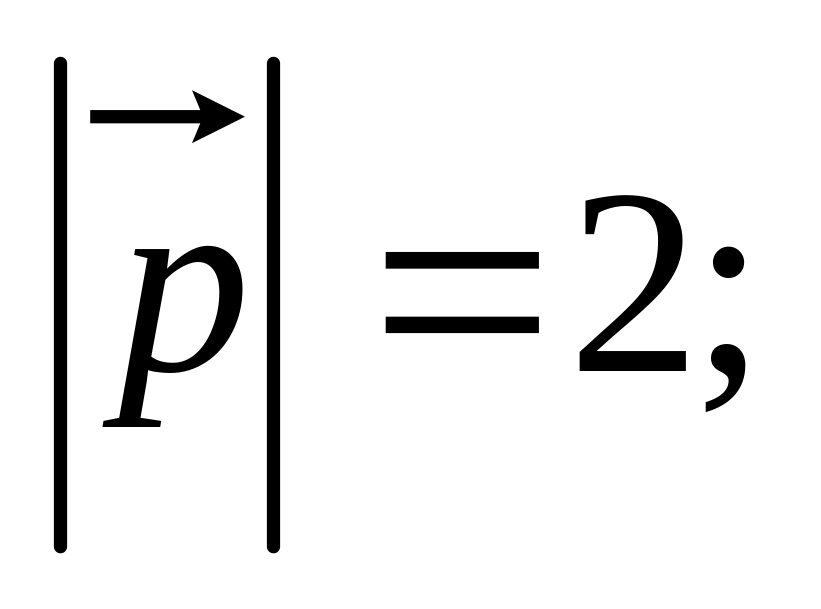
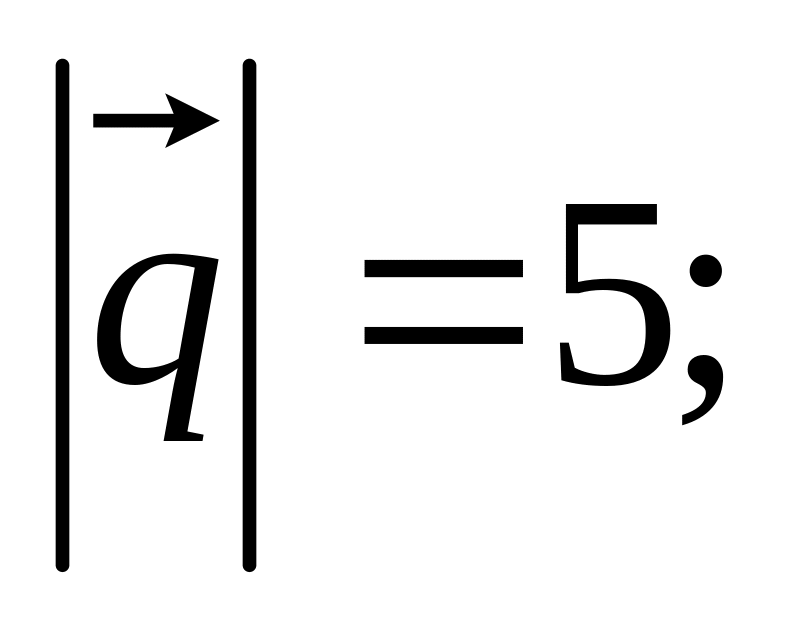
15)
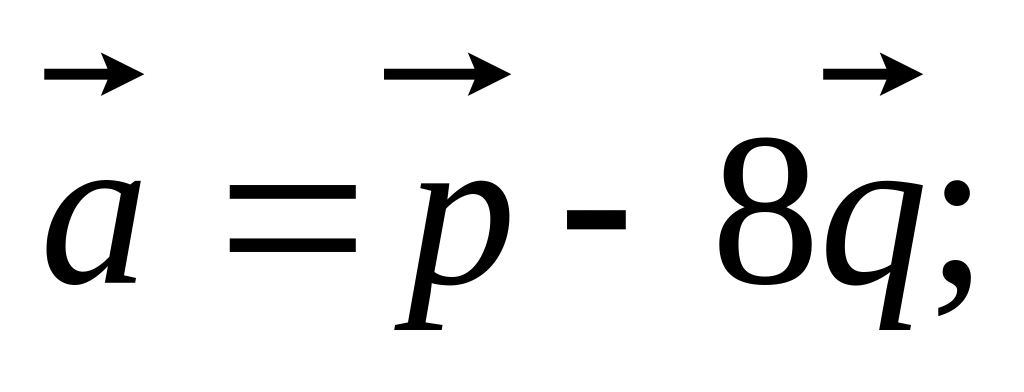
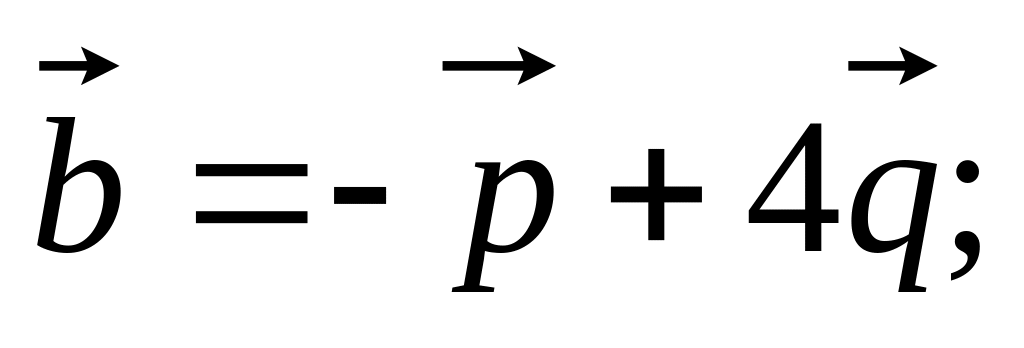
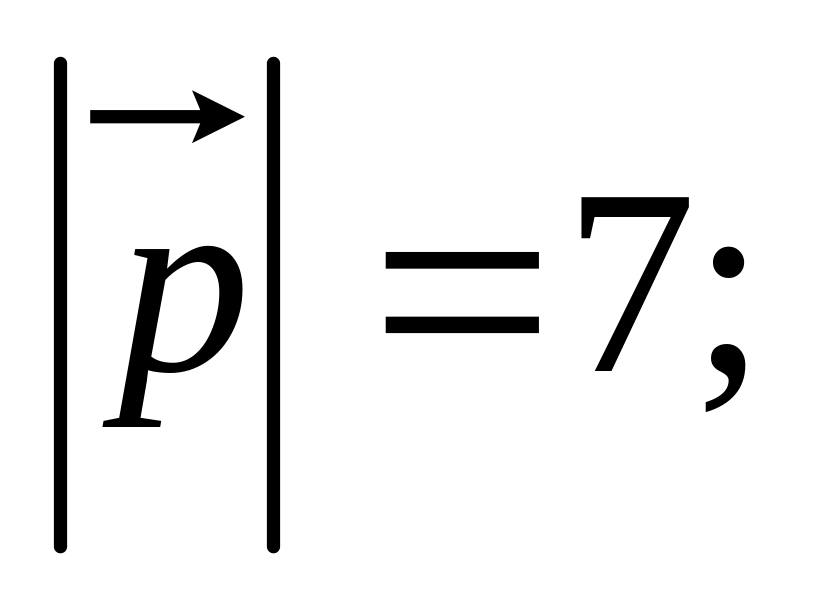
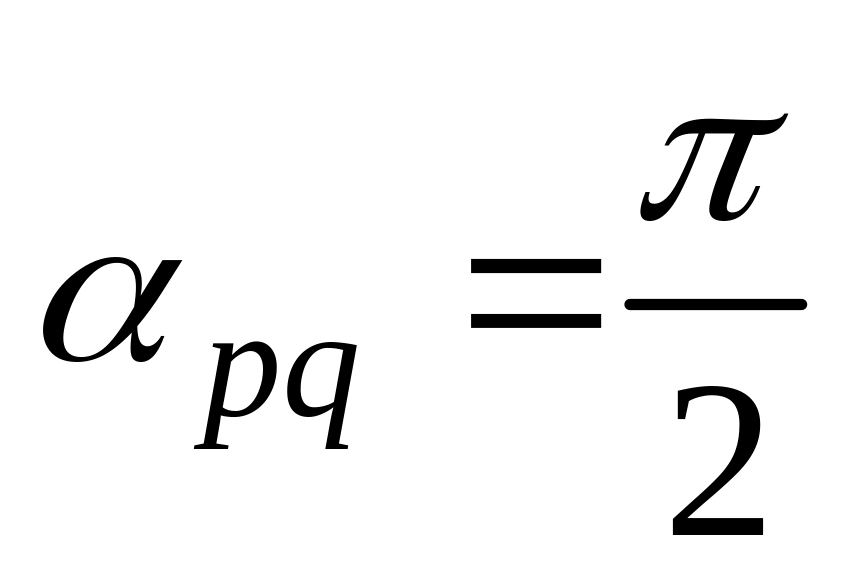
16)
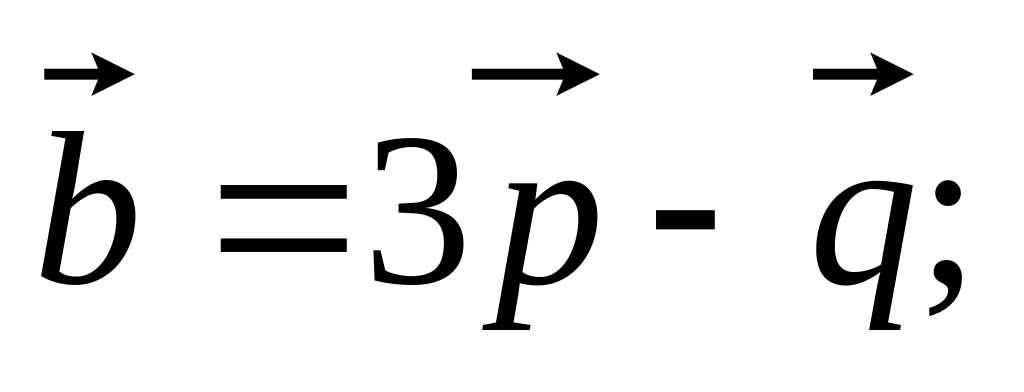
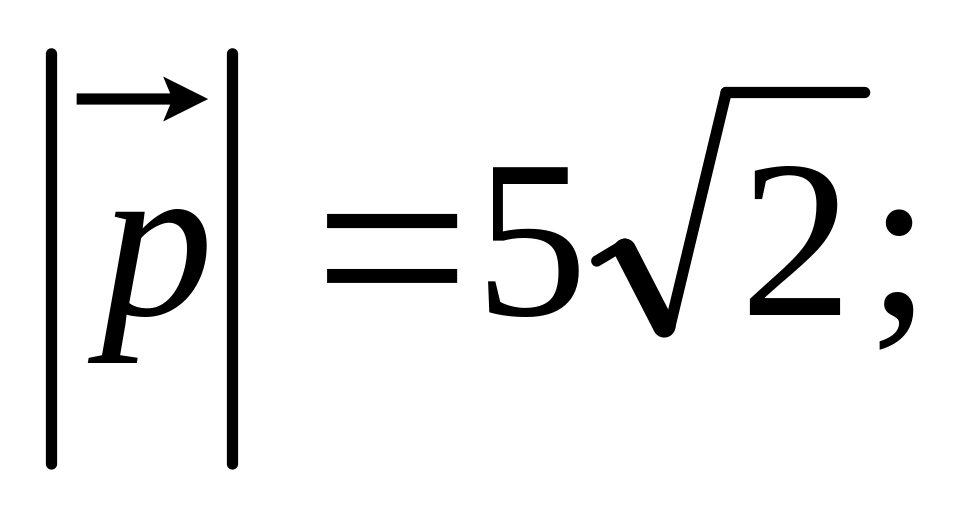
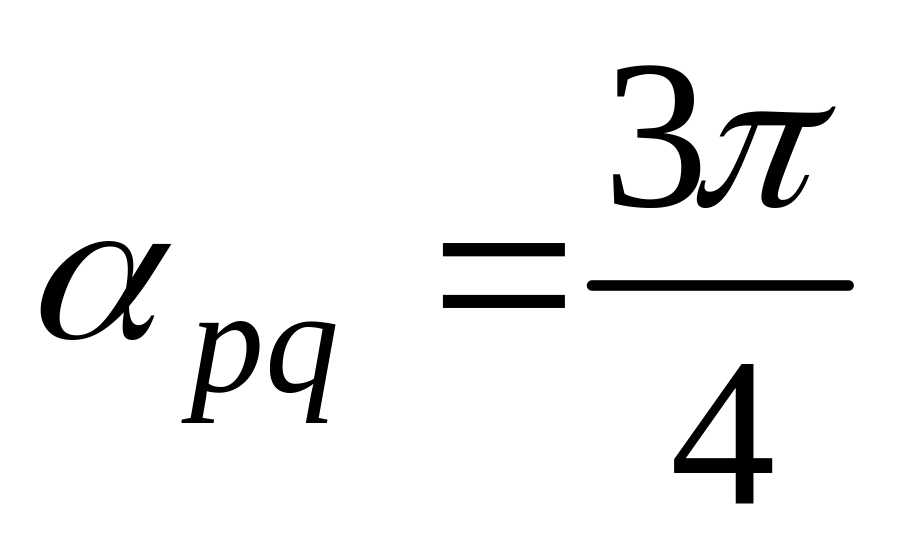
12. Показать, что тройка векторов
,
заданных своими координатами в базисе
сама является базисом. Найти координаты
вектора
в базисе
1) |
|
|
|
|
2) |
|
|
|
|
3) |
|
|
|
|
4) |
|
|
|
|
5) |
|
|
|
|
6) |
|
|
|
|
7) |
|
|
|
|
8) |
|
|
|
|
9) |
|
|
|
|
10) |
|
|
|
|
11) |
|
|
|
|
12) |
|
|
|
|
13) |
|
|
|
|
14) |
|
|
|
|
15) |
|
|
|
|
16) |
|
|
|
|
Аналитическая геометрия
13. На плоскости
заданы три точки
Составить каноническое, общее и
приведенное уравнения:
а) прямой проходящей через две точки и
б) прямой
проходящей через точку
параллельно
в) прямой проходящей через точку С перпендикулярно .
1) |
|
|
|
2) |
|
|
|
3) |
|
|
|
4) |
|
|
|
5) |
|
|
|
6) |
|
|
|
7) |
|
|
|
8) |
|
|
|
9) |
|
|
|
10) |
|
|
|
11) |
|
|
|
12) |
|
|
|
13) |
|
|
|
14) |
|
|
|
15) |
|
|
|
16) |
|
|
|
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
14. На плоскости
даны две прямые
и
Если они пересекаются, то найти координаты
точки М их пересечения и угол между
прямыми.
-
1)
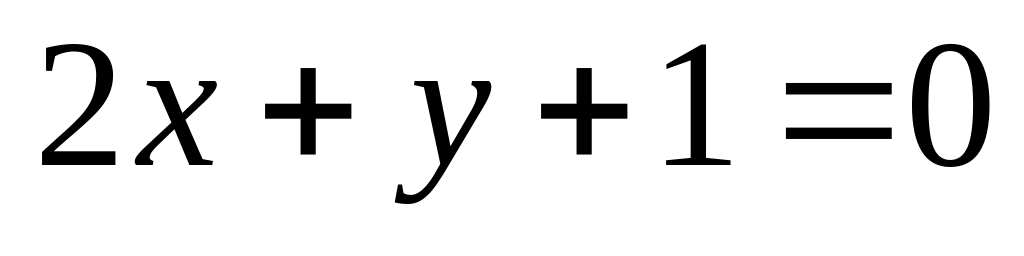
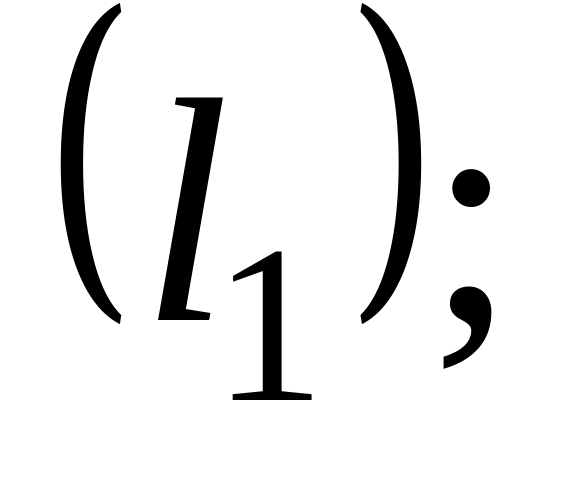
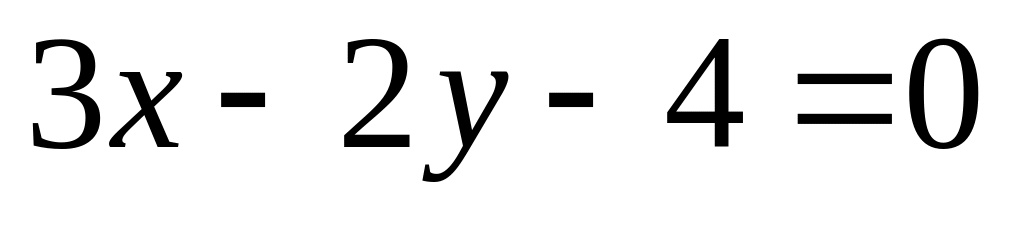
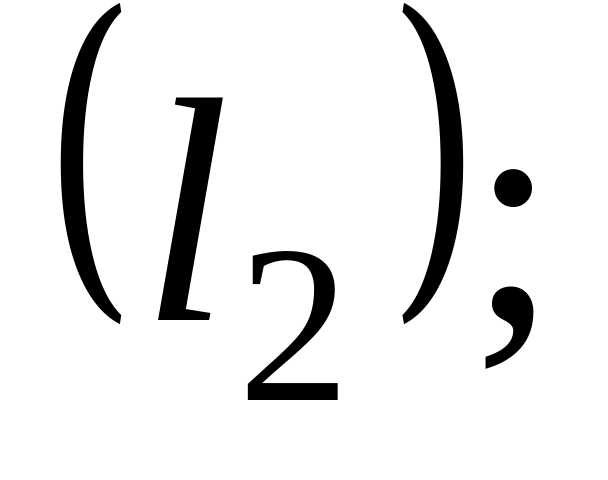
2)
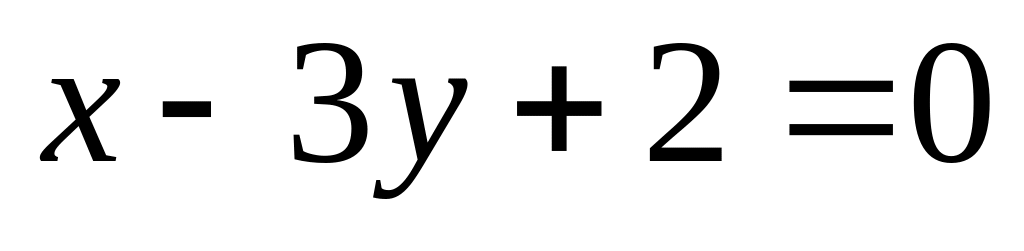
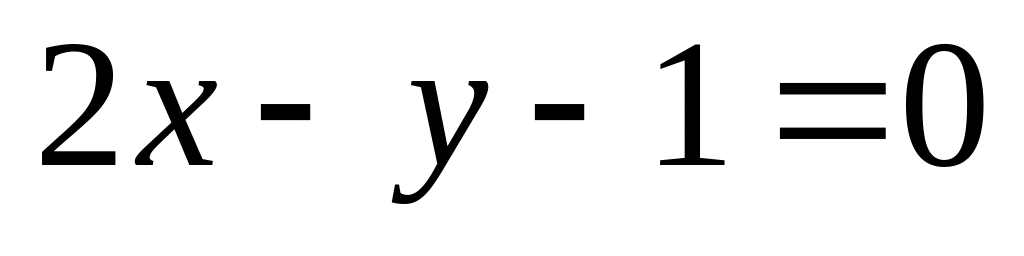
3)
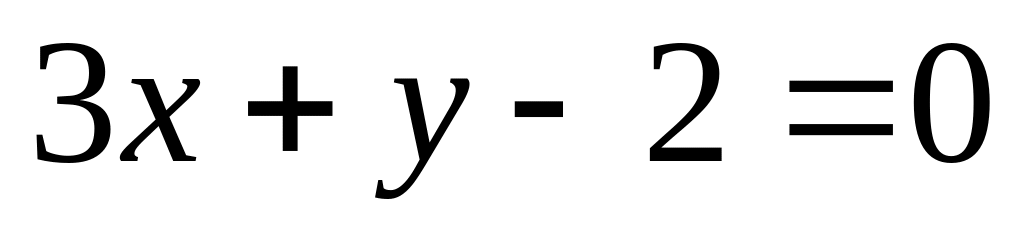
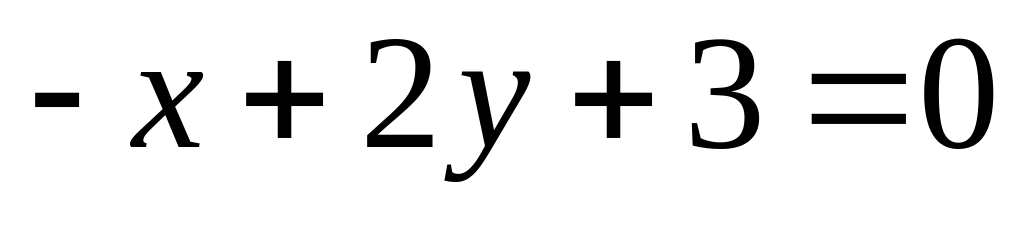
4)
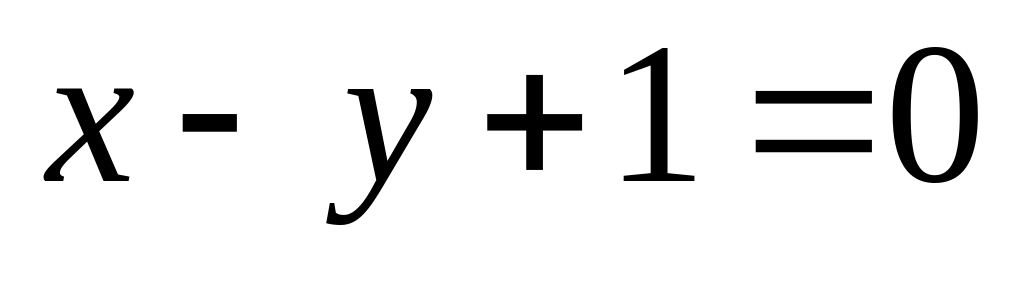
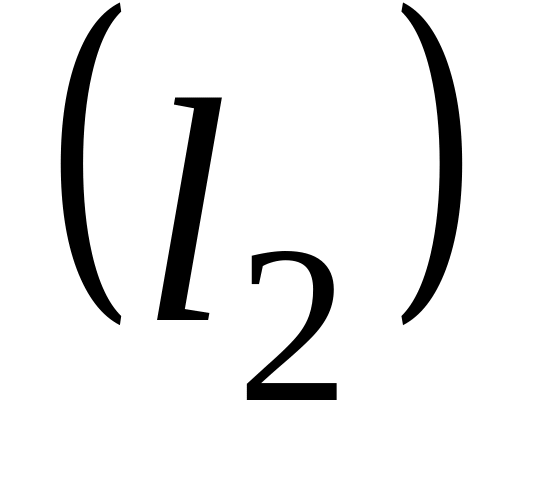
5)
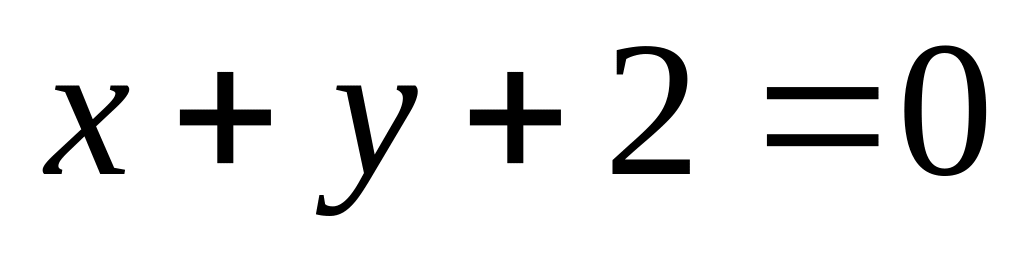
6)
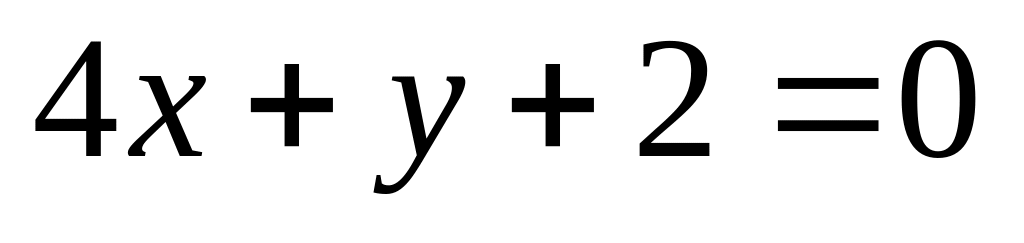
7)
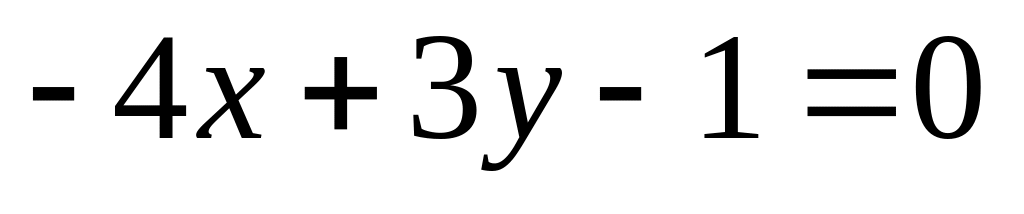
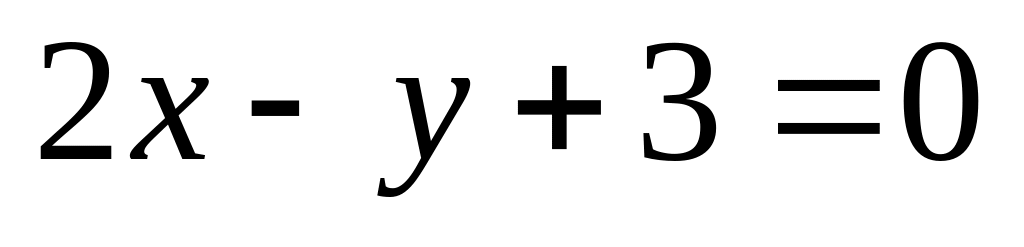
8)
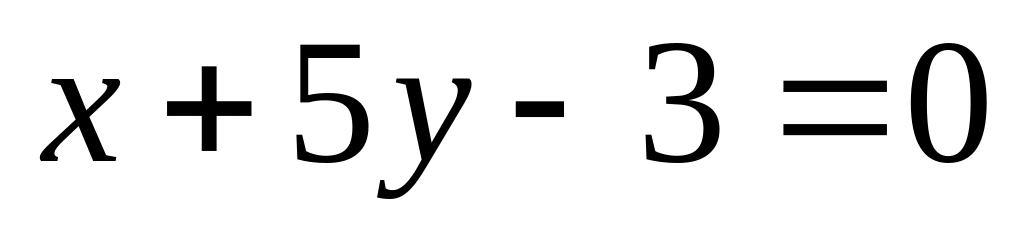
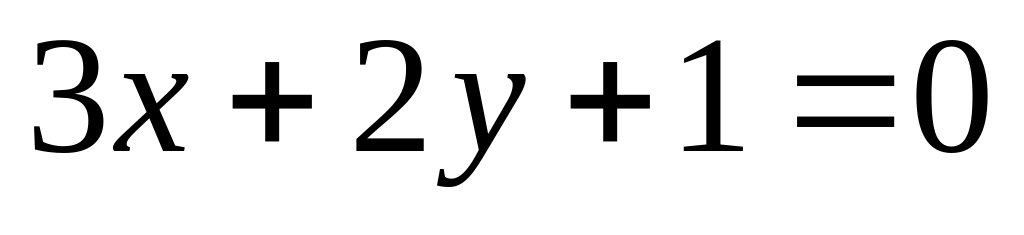
9)
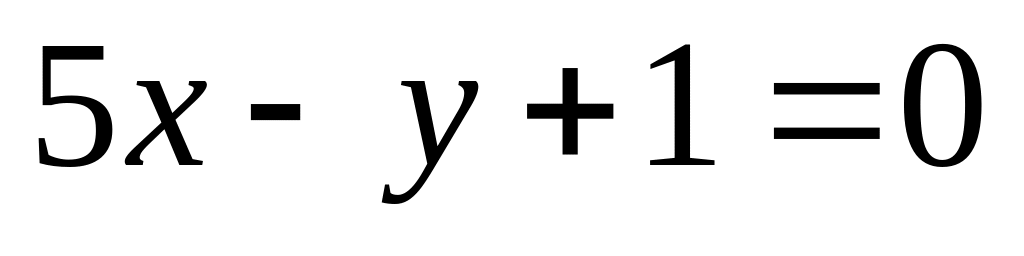
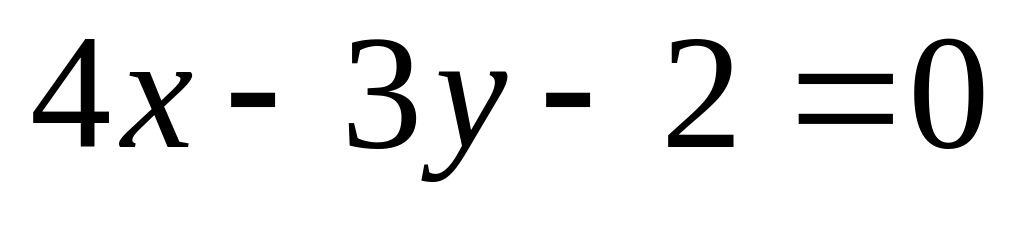
10)
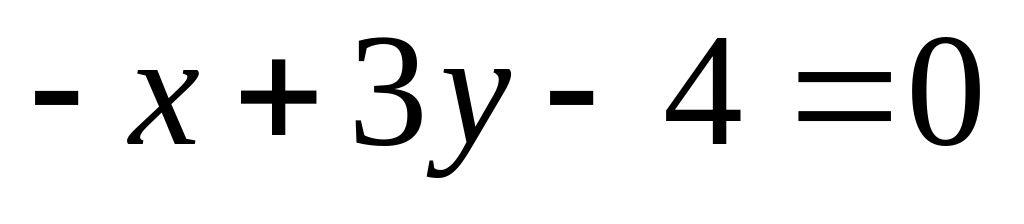
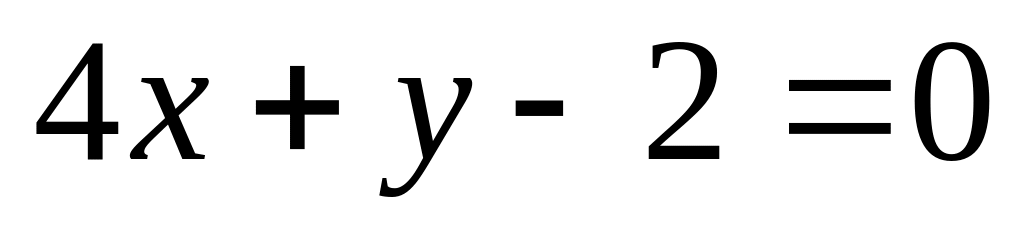
11)
12)
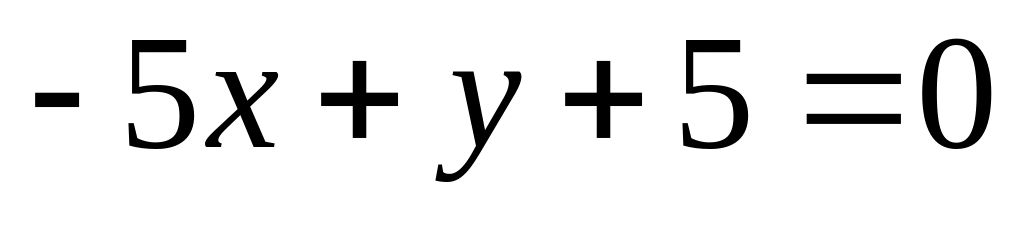
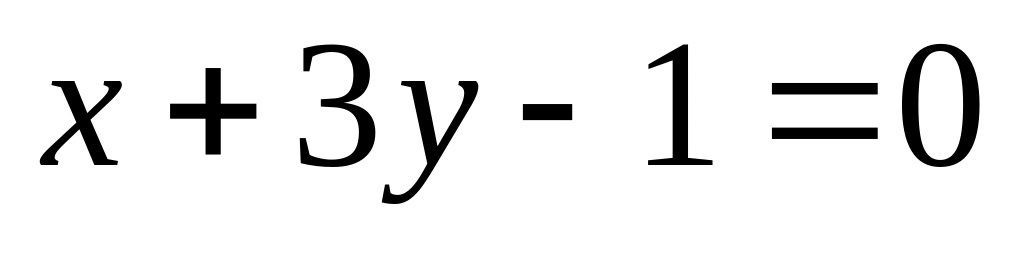
13)
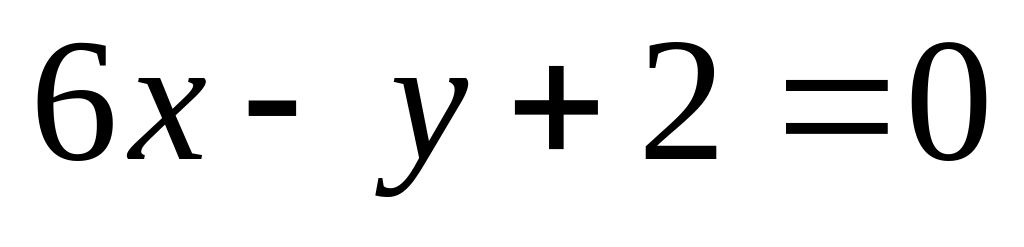
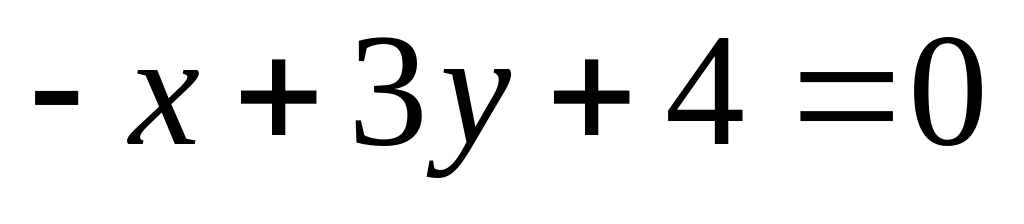
14)
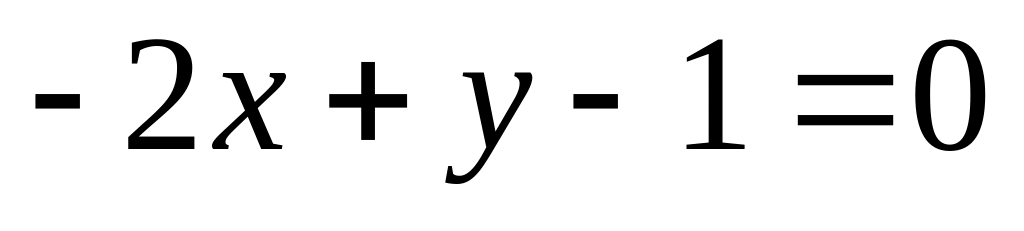
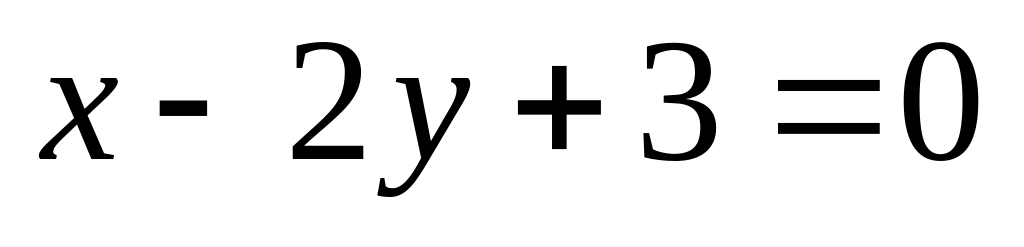
15)
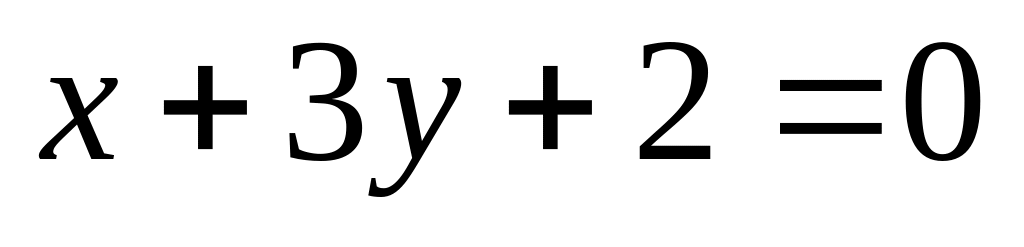
16)
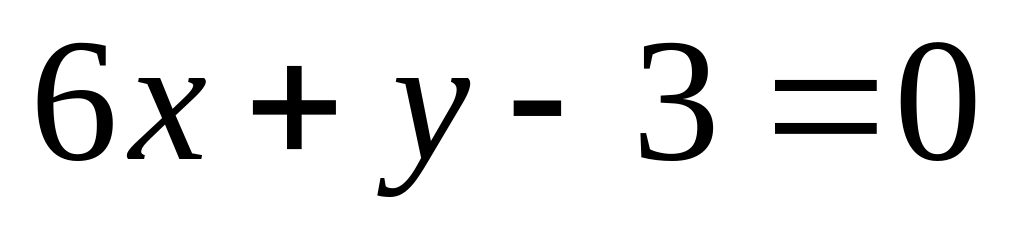
15. В пространстве
даны четыре точки
а) Составить уравнение плоскости
содержащей три точки
б) Составить уравнение плоскости
проходящей через точку
параллельно плоскости
в) Найти расстояние между плоскостями
и
Варианты значений координат точек
взять из задач п. 8 и 10.
16. Даны две плоскости
и
Найти угол между ними.
-
1)
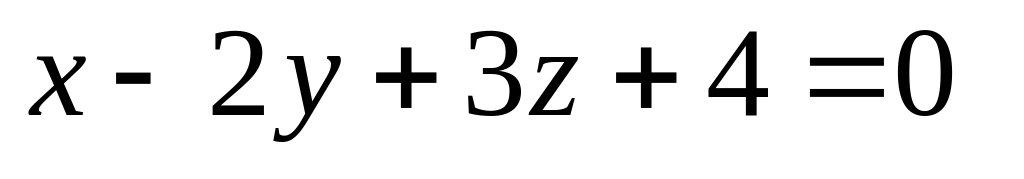
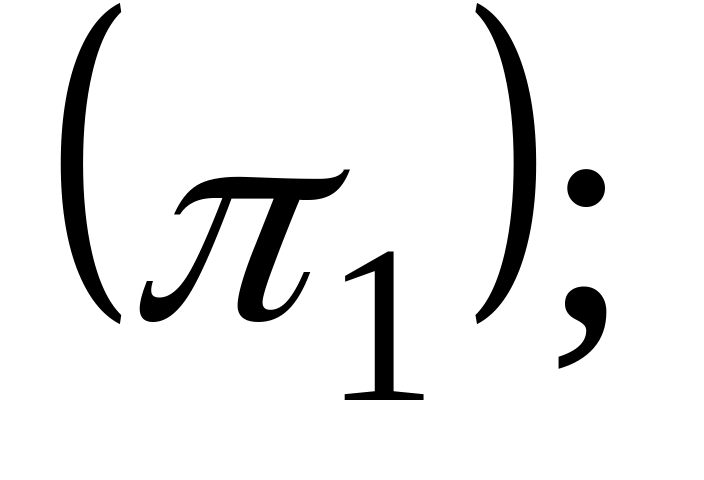
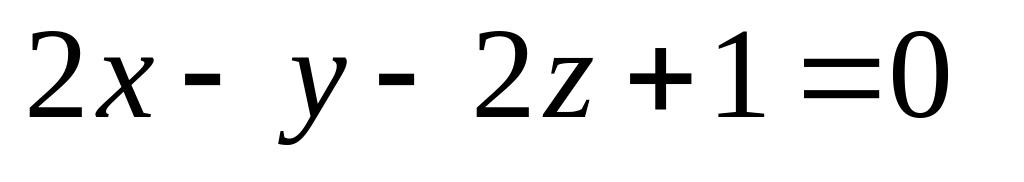
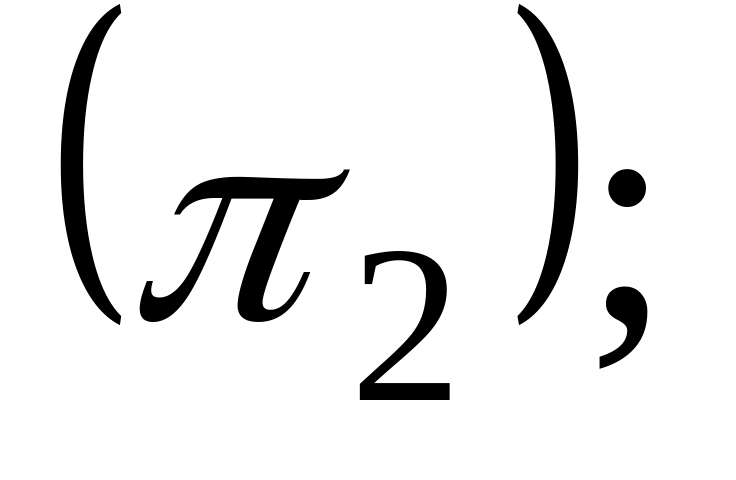
2)
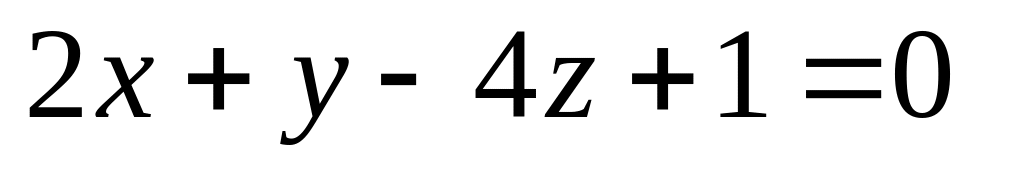
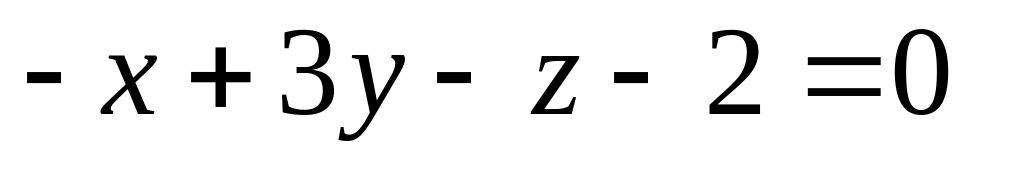
3)
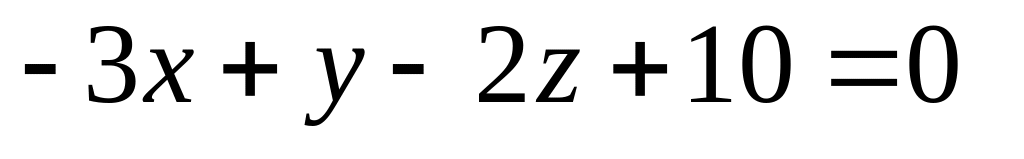
4)
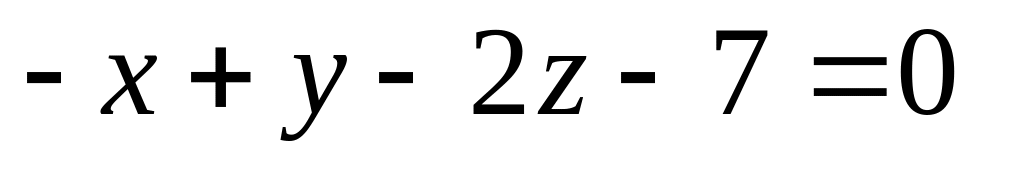
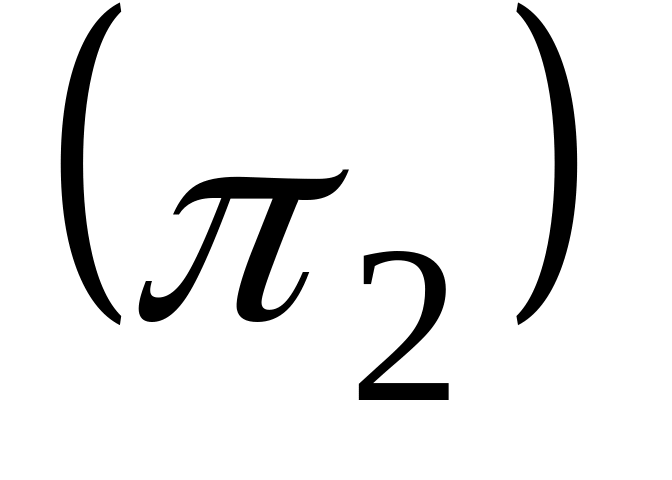
5)
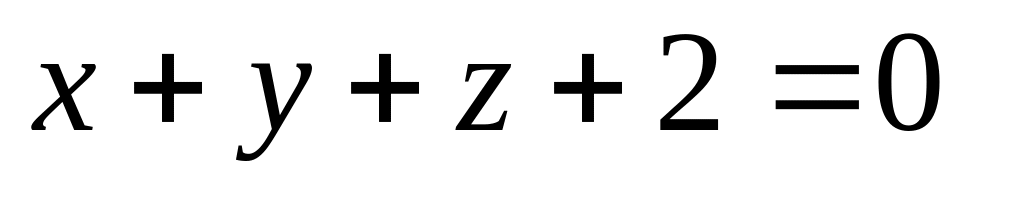
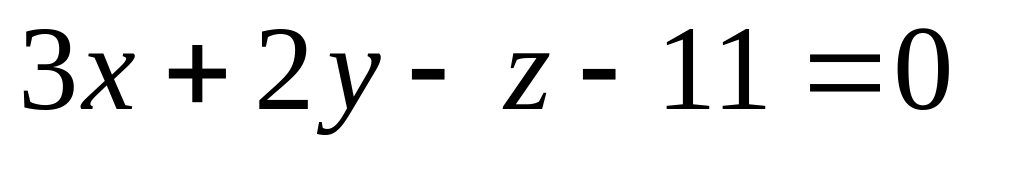
6)
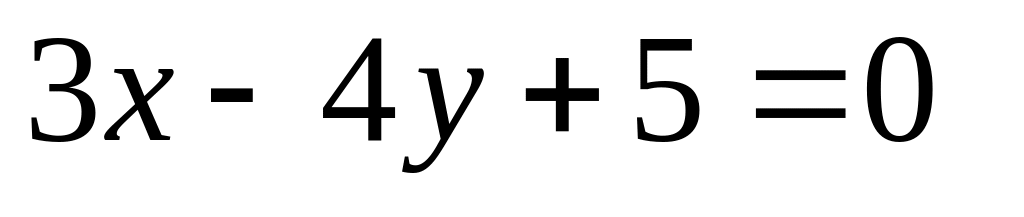
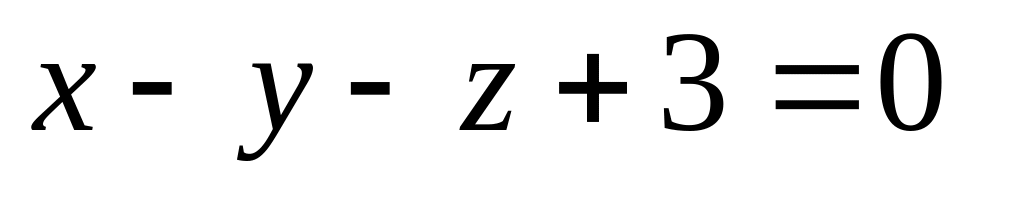
7)
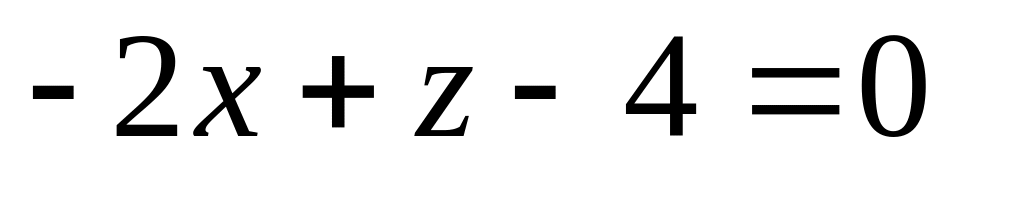
8)
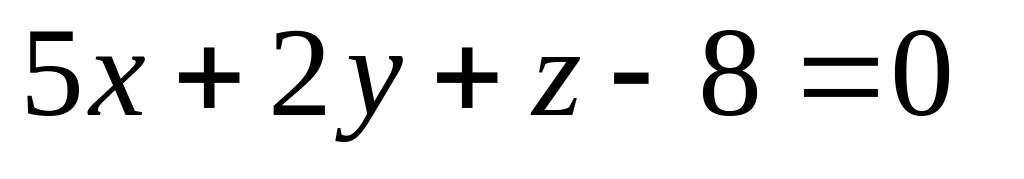
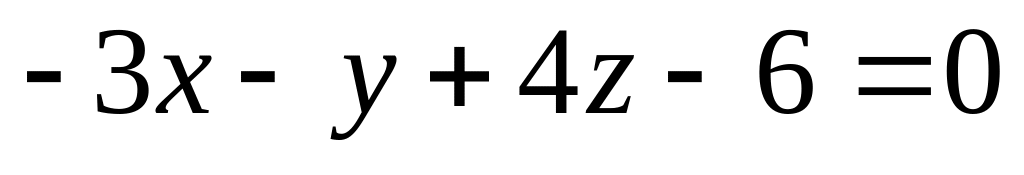
9)
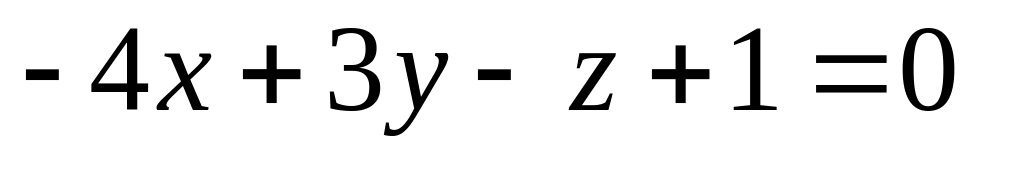
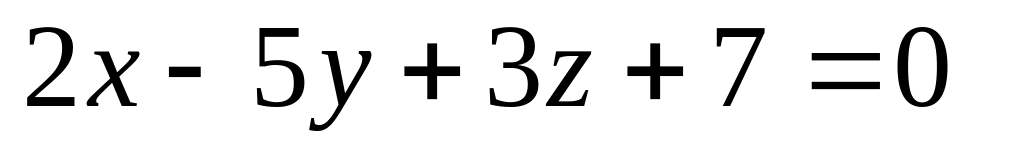
10)
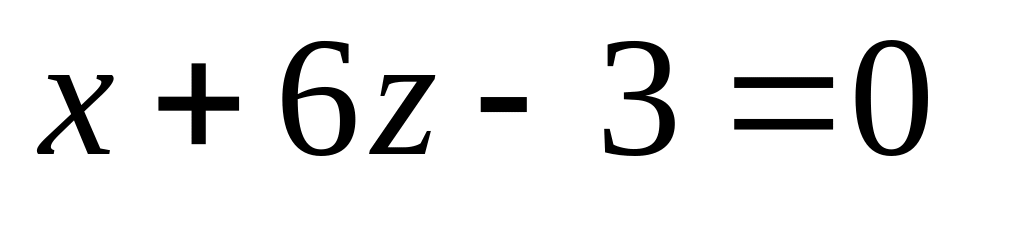
11)
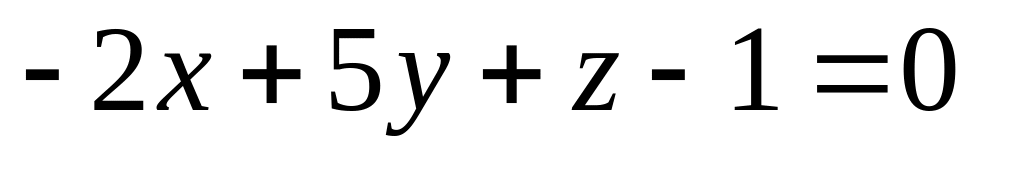
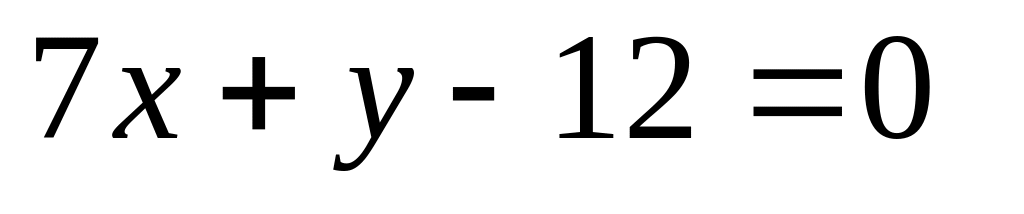
12)
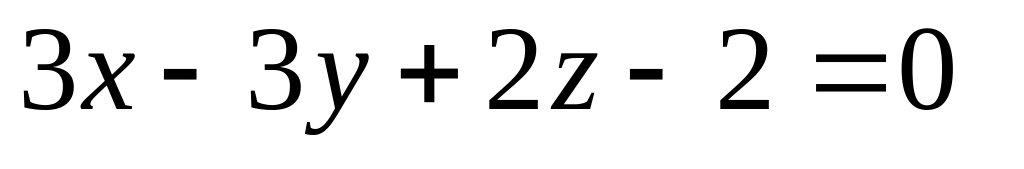
13)
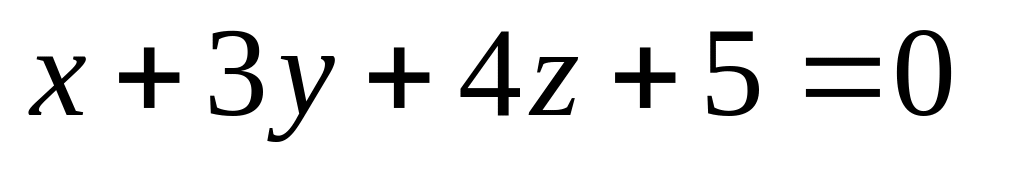
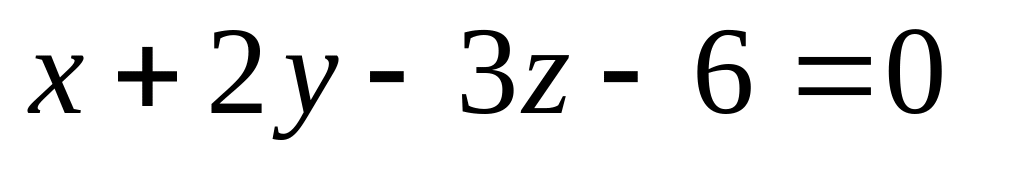
14)
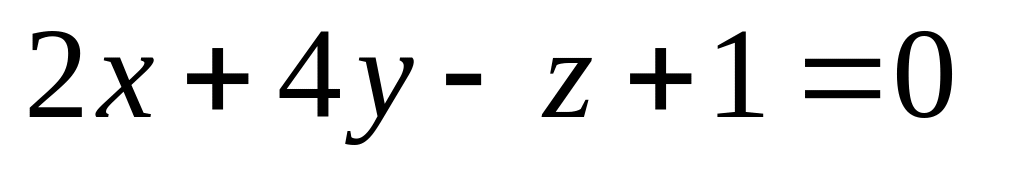
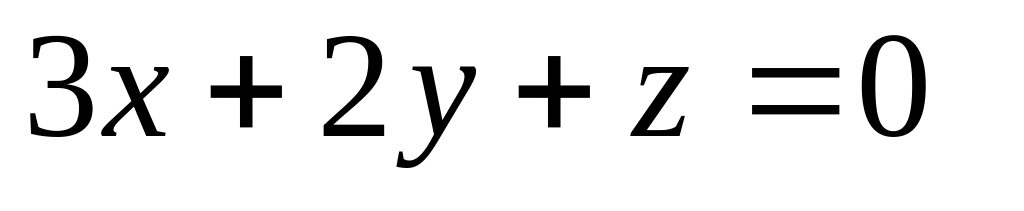
15)
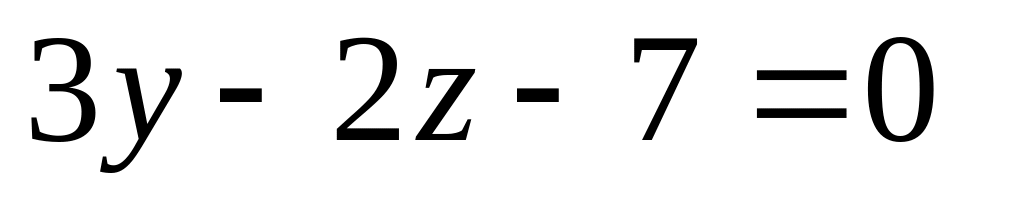
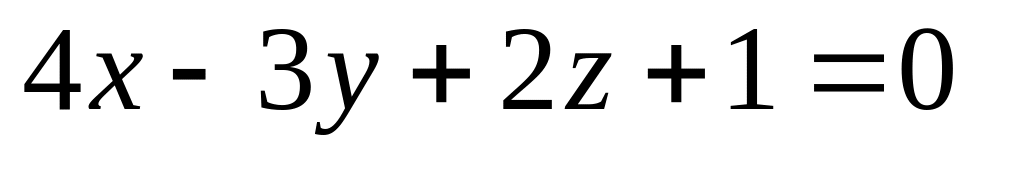
16)
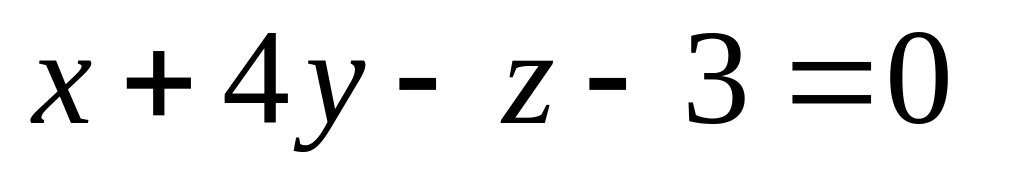
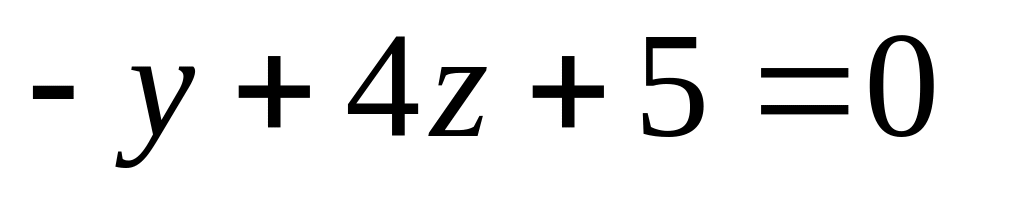
17. Даны две плоскости
и
а также точка
Составить уравнение плоскости
проходящей через точку
перпендикулярно обеим плоскостям
и
Варианты уравнений плоскостей взять
из п.16, а соответствующие им варианты
значений координат точки М следующие:
18. В пространстве
составить канонические и общие уравнения
прямой, проходящей через две заданные
точки
и
.
-
1)
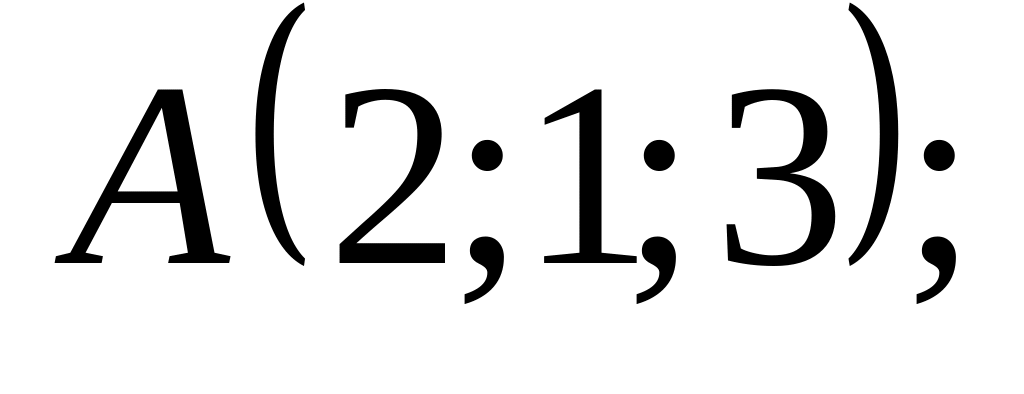
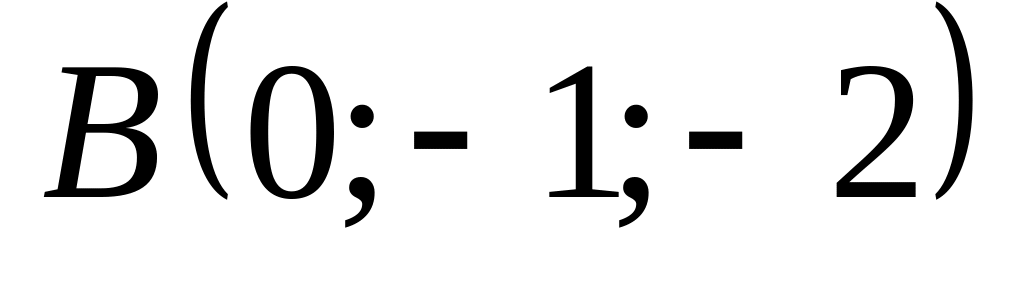
2)
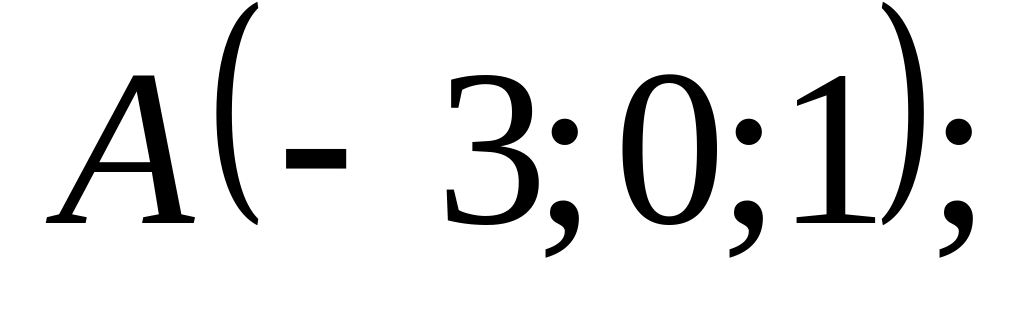
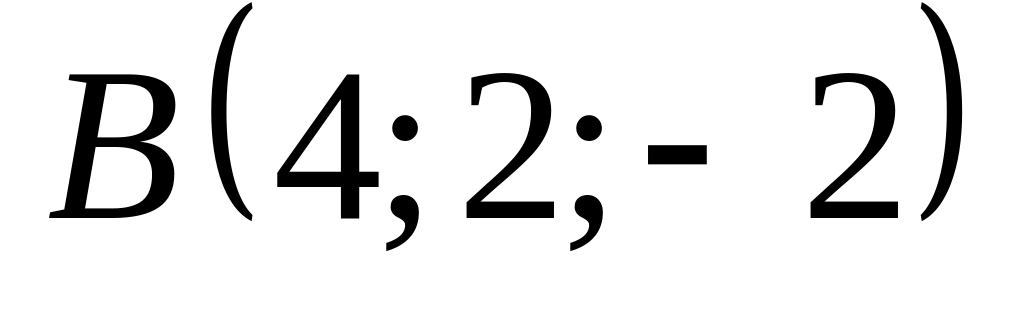
3)
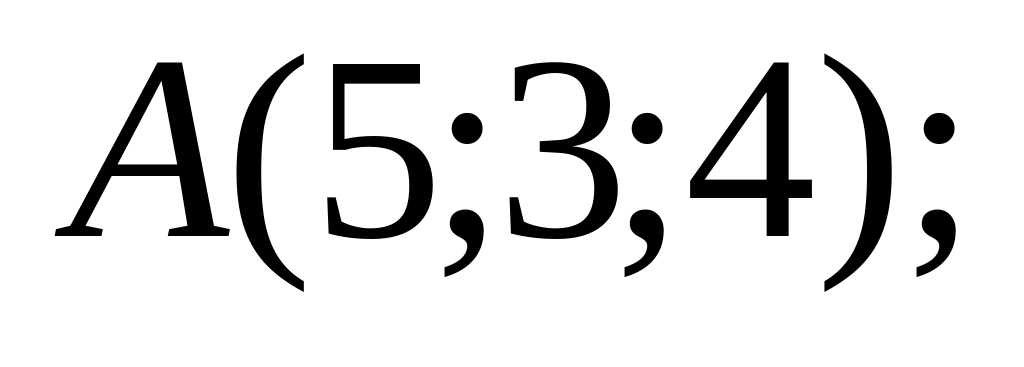
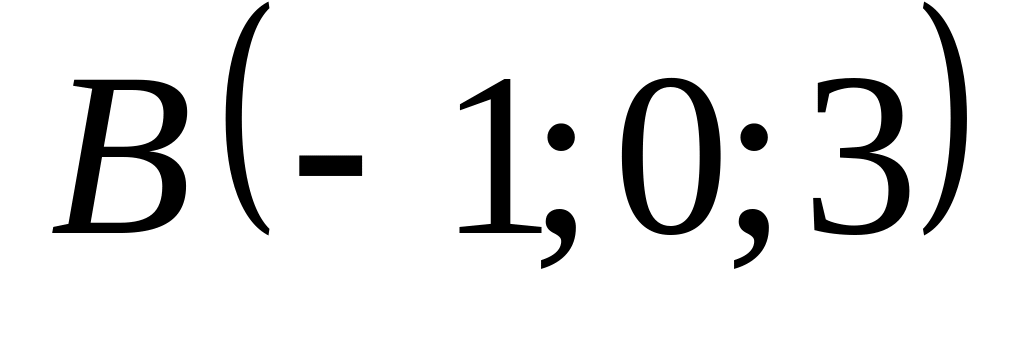
4)
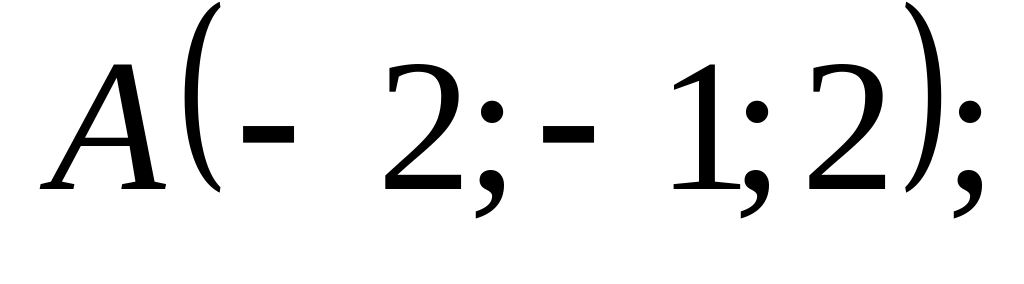
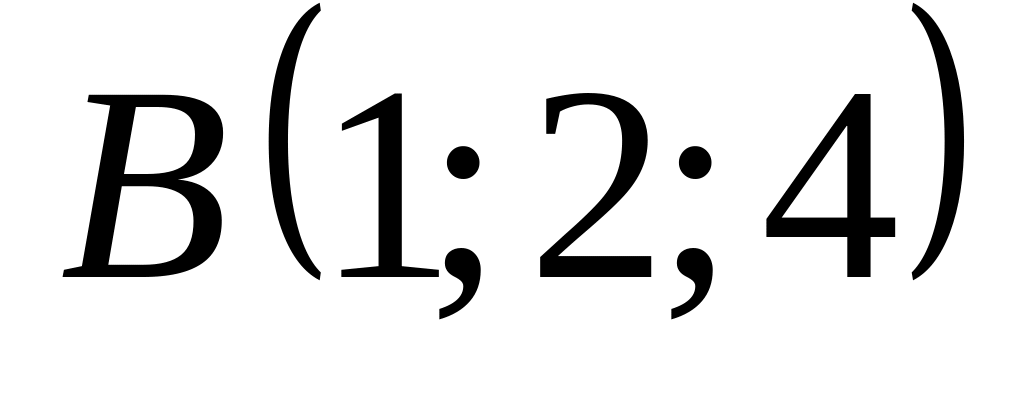
5)
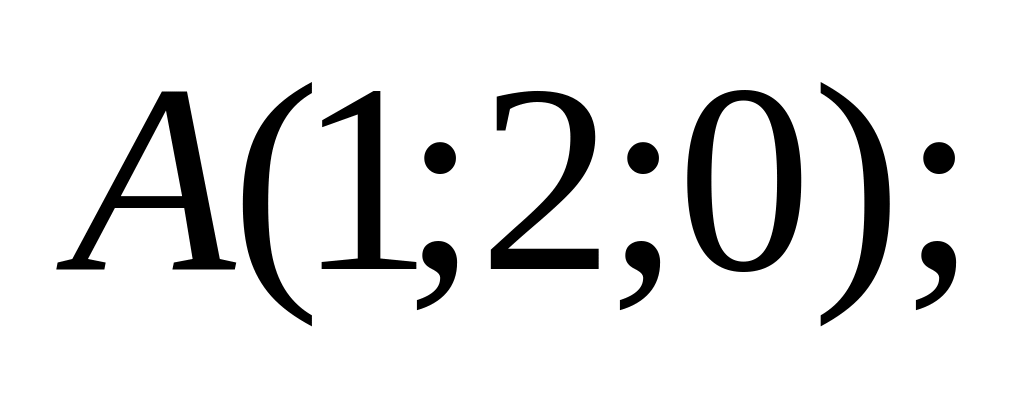
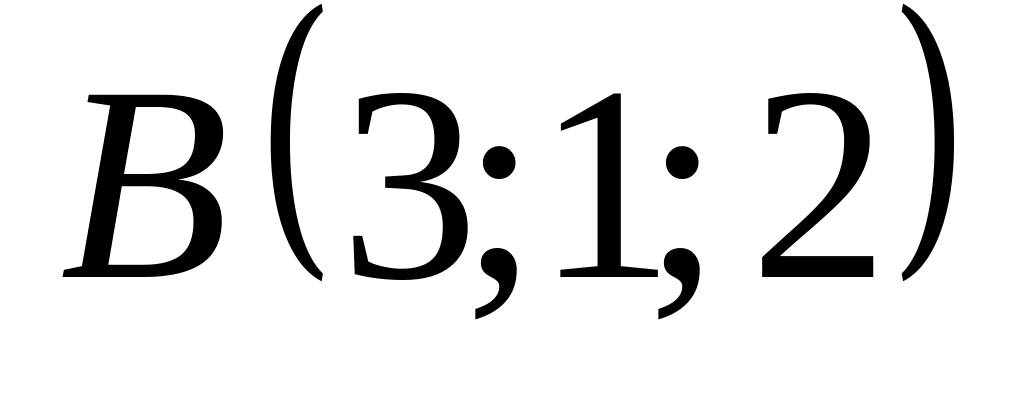
6)
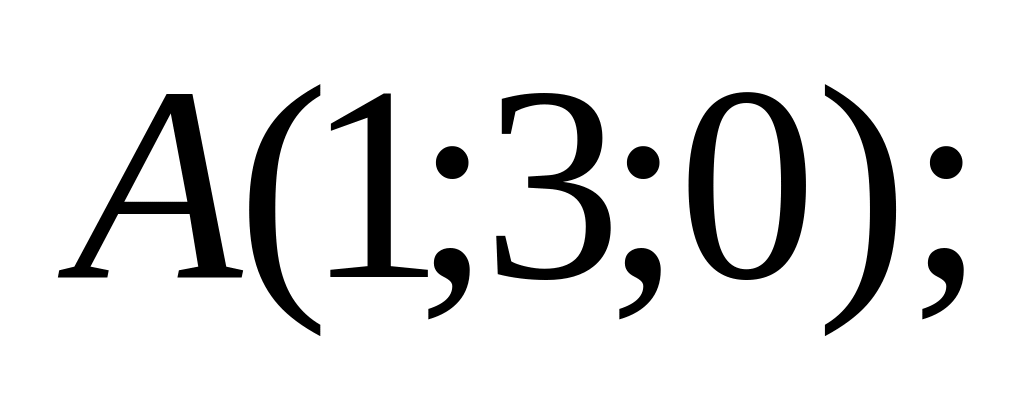
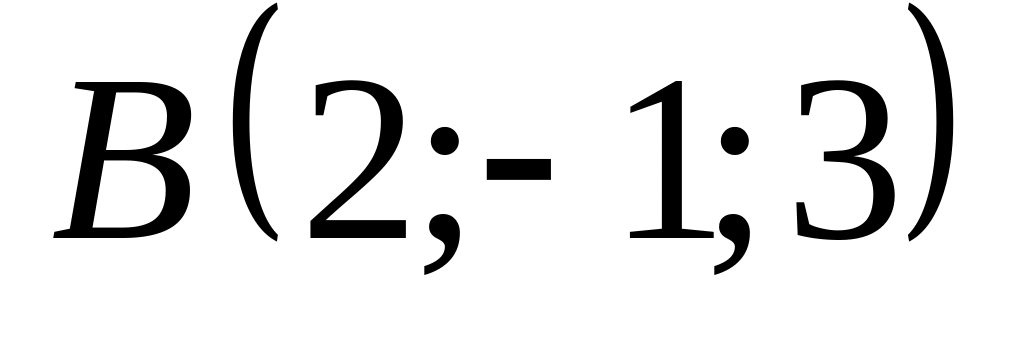
7)
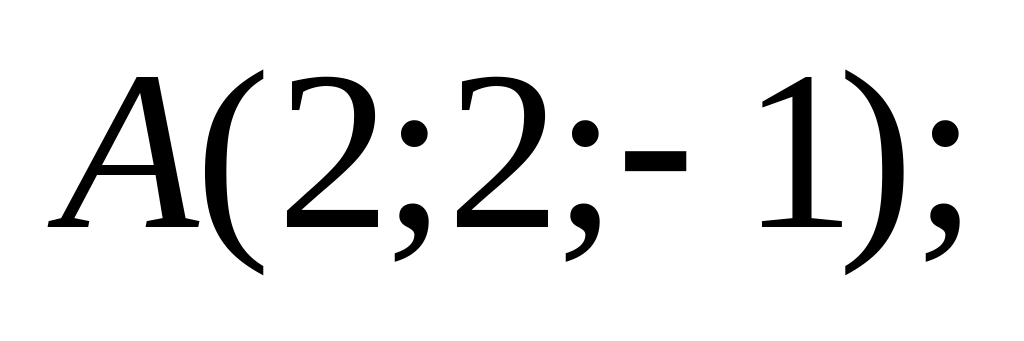
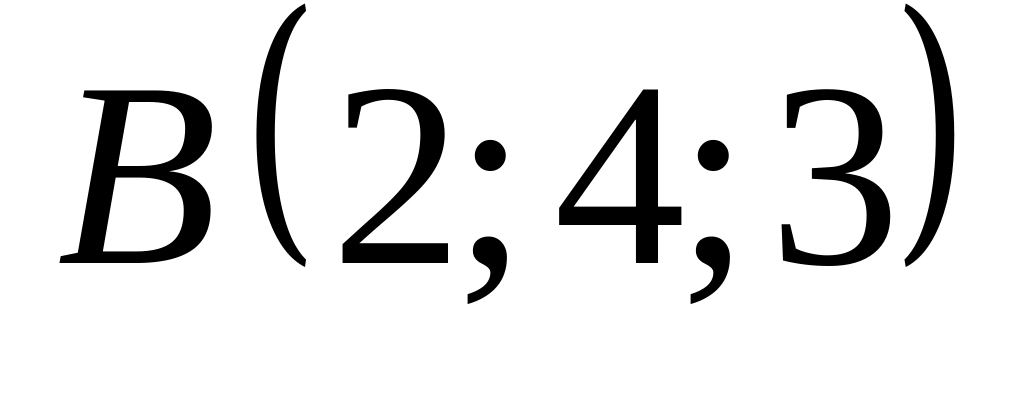
8)
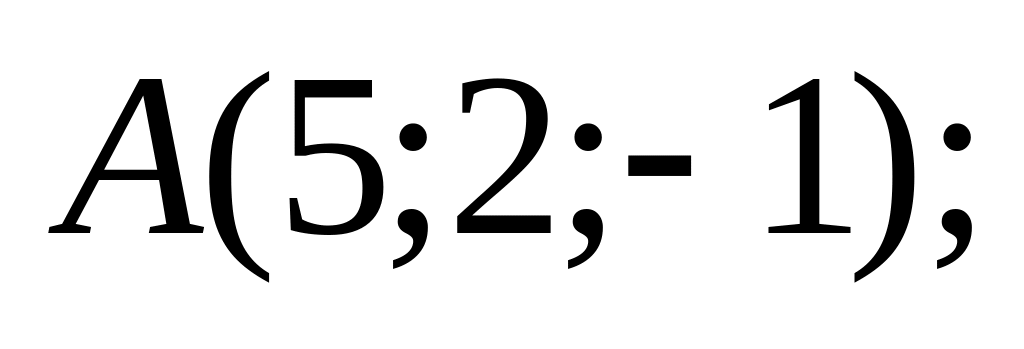
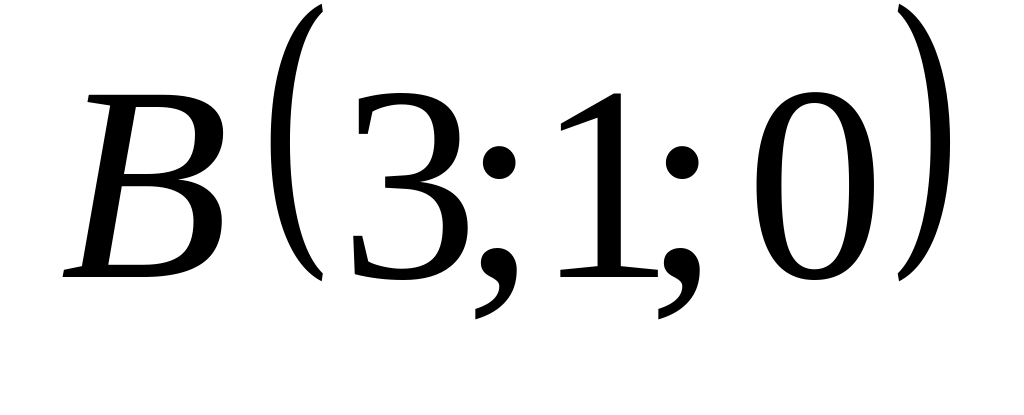
9)
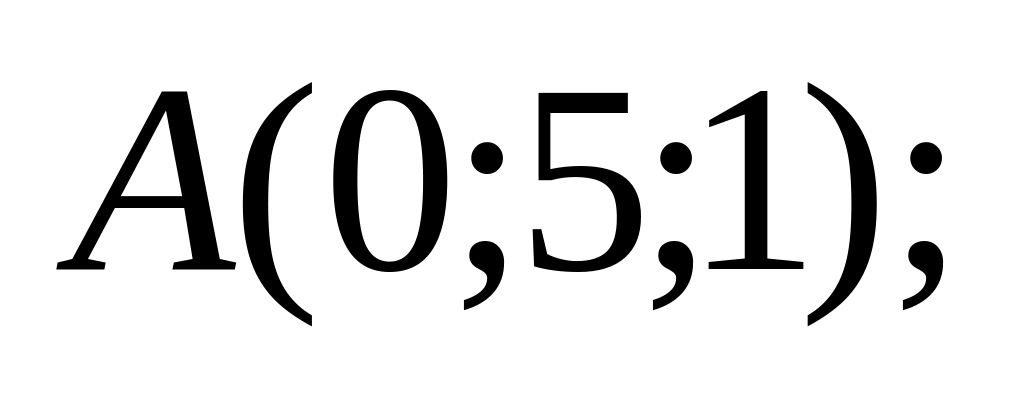
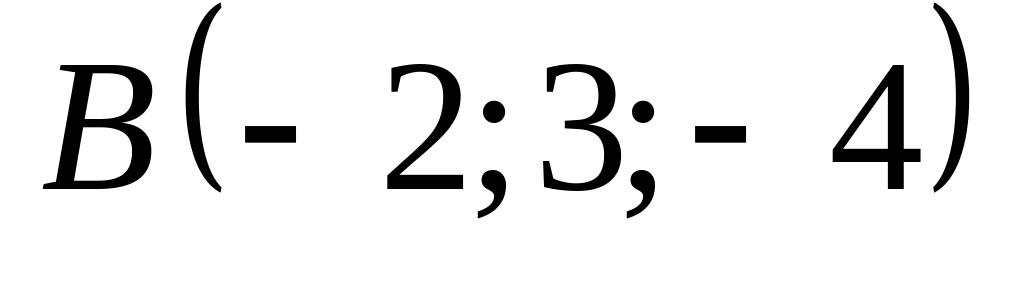
10)
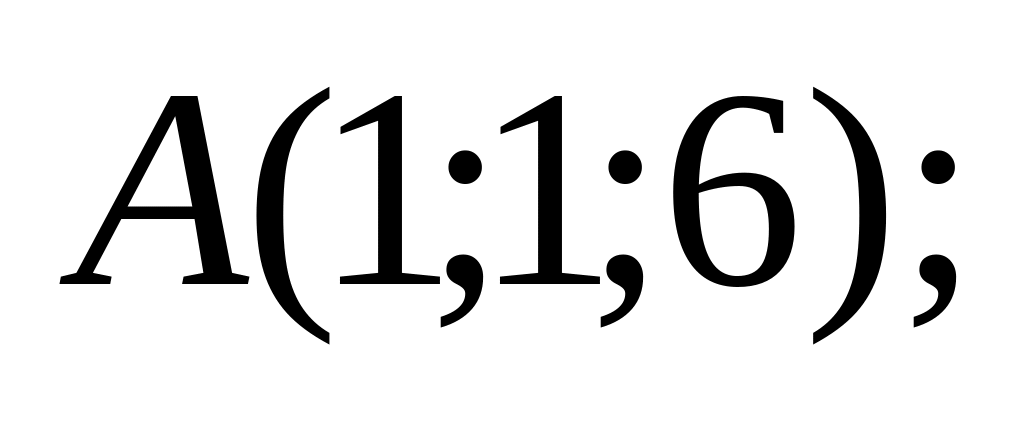
11)
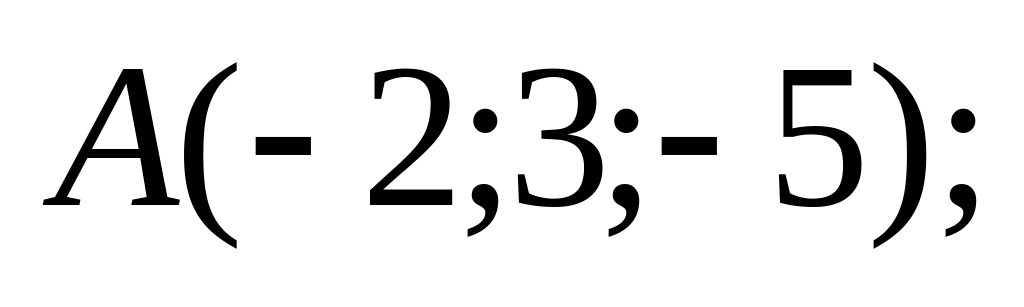
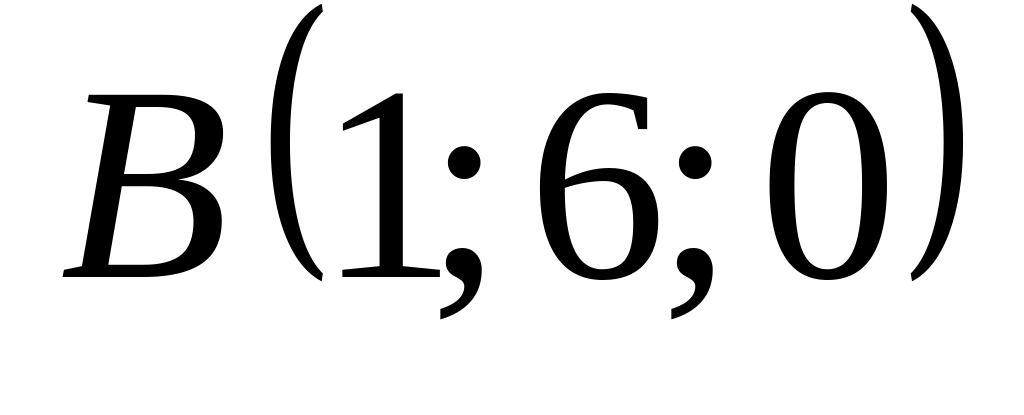
12)
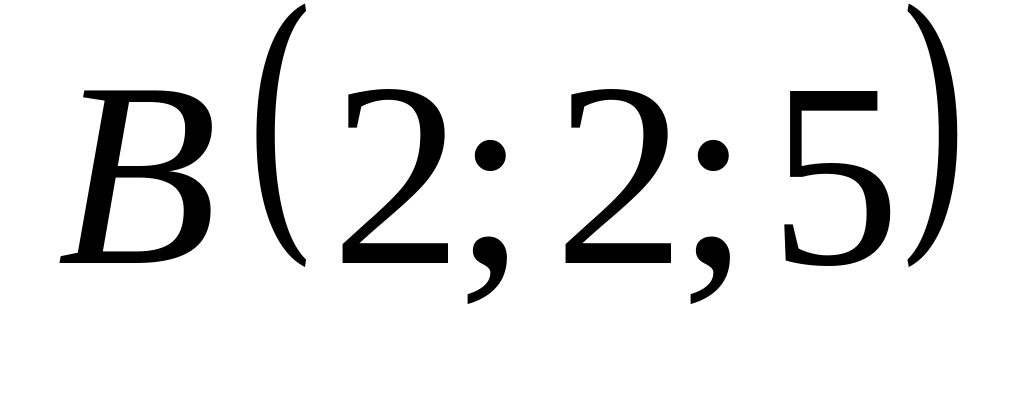
13)
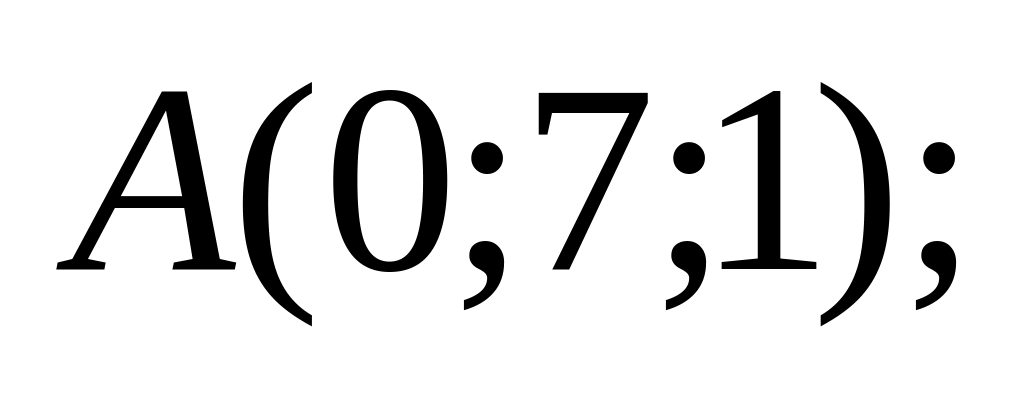
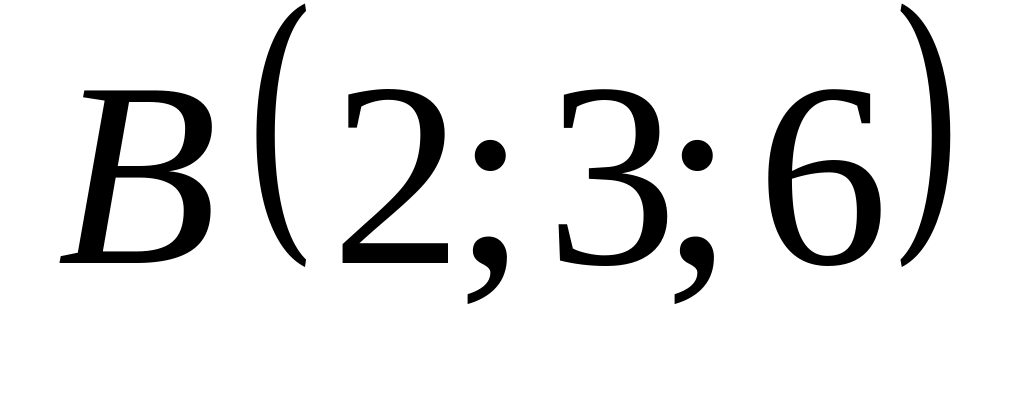
14)
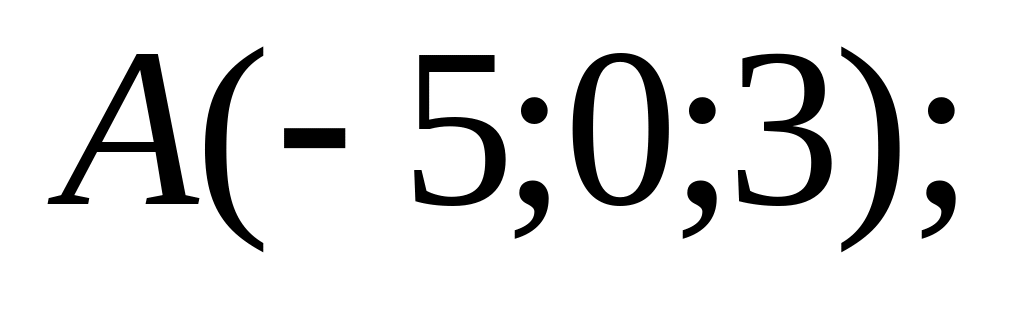
15)
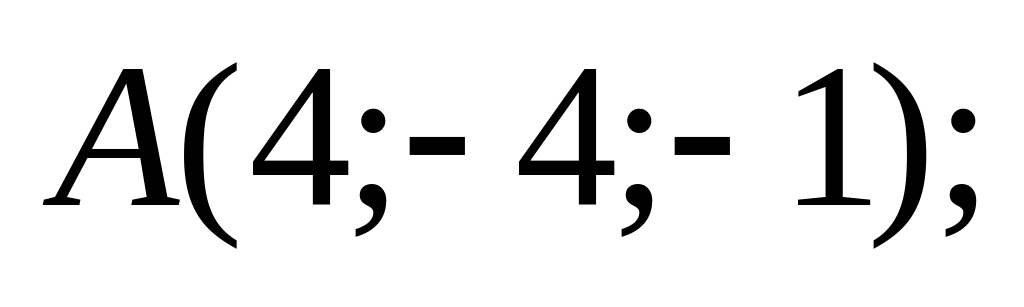
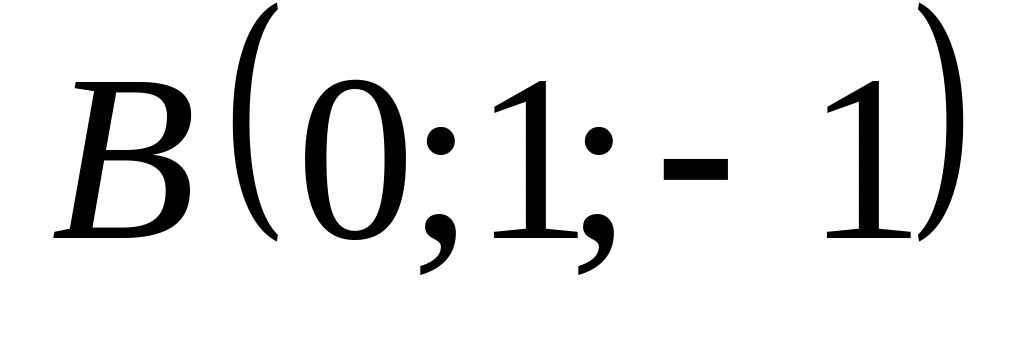
16)
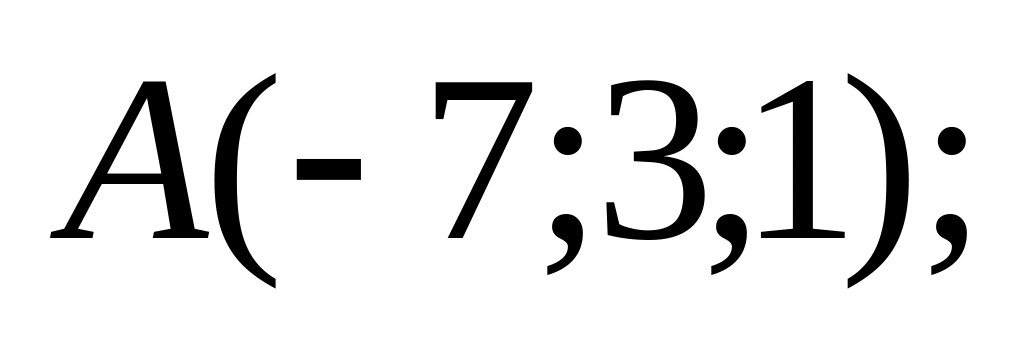
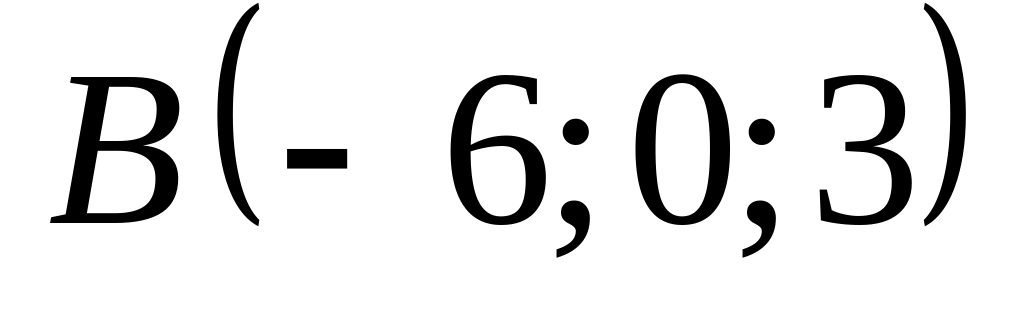
19. Даны две плоскости
Составить канонические уравнения прямой
– линии их пересечения. Варианты
уравнений плоскостей взять из пункта
16. Так, например, для первого варианта
общими уравнениями прямой
будут
20. В пространстве своими каноническими уравнениями заданы две прямые и , а также задана точка .
а) Составить канонические уравнения прямой проходящей через точку перпендикулярно обеим прямым и
б) Составить уравнение плоскости проходящей через точку параллельно обеим прямым и
1) |
|
|
|
|
|
2) |
|
|
|
|
|
3) |
|
|
|
|
|
4) |
|
|
|
|
|
5) |
|
|
|
|
|
6) |
|
|
|
|
|
7) |
|
|
|
|
|
8) |
|
|
|
|
|
9) |
|
|
|
|
|
10) |
|
|
|
|
|
11) |
|
|
|
|
|
12) |
|
|
|
|
|
13) |
|
|
|
|
|
14) |
|
|
|
|
|
15) |
|
|
|
|
|
16) |
|
|
|
|
|
21. В пространстве
задана прямая
и плоскость
Найти угол между ними и координаты точки
их пересечения. Для каждого варианта в
качестве уравнения прямой
взять уравнение прямой
из п. 20, а в качестве уравнения плоскости
взять уравнение плоскости
из п. 16.
22. Задана плоскость
и точка
Найти координаты проекции
точки
на плоскость
Для каждого варианта в качестве уравнения
плоскости
взять уравнение плоскости
из п. 16; значения координат точки
взять из задач п.20.