
- •Глава III. Теория вероятностей
- •3.1. Основные понятия
- •1. Алгебра событий
- •2. Вероятностное пространство
- •3. Теоремы сложения и умножения вероятностей
- •4. Независимость событий
- •5. Классическое вероятностное пространство
- •6. Элементы комбинаторики
- •7. Геометрические вероятности
- •Напомним соответствующие определения:
- •8. Упражнения и задачи
- •3.2. Контрольная работа №1 по теории вероятностей
- •3.3. Случайные величины
- •2. Дискретные случайные величины
- •3. Примеры дискретных случайных величин
- •Биноминальное распределение
- •Распределение Пуассона.
- •4. Непрерывные случайные величины
- •1. Свойства плотности распределения
- •2. Приведем примеры непрерывных распределений
- •5. Числовые характеристики случайных величин
- •1. Числовые характеристики дискретных случайных величин
- •2. Числовые характеристики непрерывных случайных величин
- •3. Свойства математического ожидания случайной величины
- •4. Свойства дисперсии случайной величины
- •5. Рассмотрим практические упражнения.
- •6. Формула Лапласа
- •1. Локальная формула Муавра-Лапласа
- •2. Интегральная формула Муавра-Лапласа
- •7. Распределение Пуассона
- •8. Контрольная работа №2 по теории вероятностей
- •Основная литература
6. Формула Лапласа
Вернемся к нормальному распределению. Пусть случайная величина Х распределена по нормальному закону. Плотность распределения имеет вид
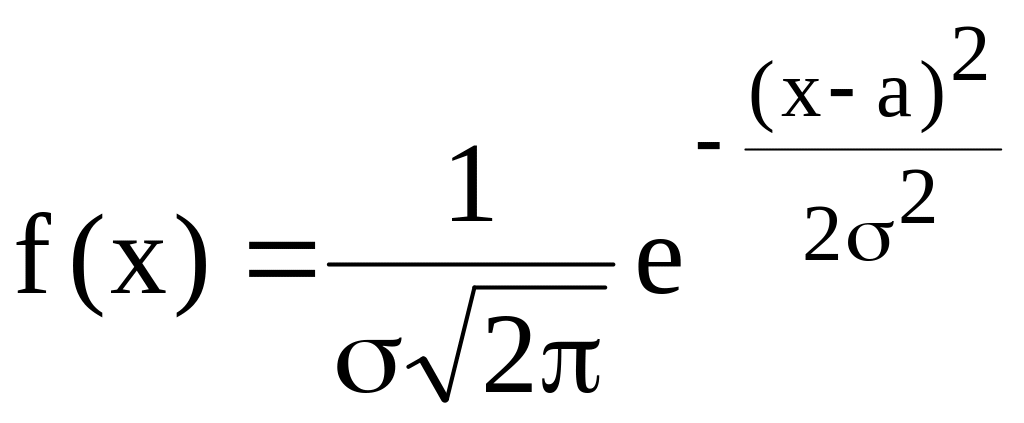 .
При этом М(Х) = а,
.
При этом М(Х) = а,
![]() ,
,
![]() .
.
Итак, второй
параметр
выражает среднеквадратическое отклонение
нормального распределения. Определим
вероятность попадания нормальной
случайной величины в интервал
![]() по формуле Лапласа
по формуле Лапласа
![]() ,
,
где
![]() ,
где Ф (t) – функция Лапласа.
,
где Ф (t) – функция Лапласа.
Пример 1. На
прядильной фабрике вырабатывается
пряжа, средняя прочность образцов
которой равна 260 сн;
![]() .
Прочность как случайная величина
приближенно следует нормальному закону
распределения. Определить долю образцов
пряжи с прочностью от 224 сн до 287 сн.
.
Прочность как случайная величина
приближенно следует нормальному закону
распределения. Определить долю образцов
пряжи с прочностью от 224 сн до 287 сн.
Поскольку прочность образцов пряжи Х согласно условию имеет приближенно нормальное распределение, поэтому можно использовать формулу Лапласа. В нашем случае параметры распределения такие: а=260 сн, и .
Причем
![]() .
Находим сначала
.
Находим сначала
![]()
![]() .
.
Итак, по формуле Лапласа имеем
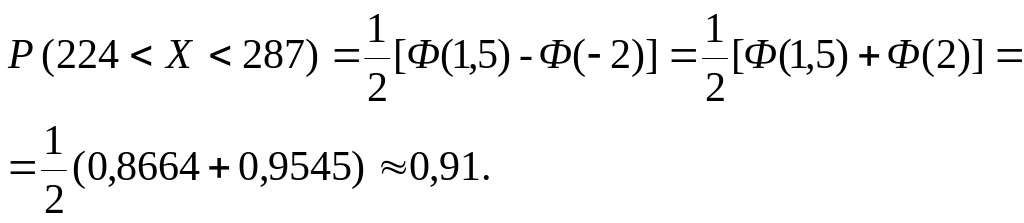
Значения функции Лапласа Ф (1,5) и Ф (2) нашли по таблице значений функции Лапласа.
Пример 2. Средняя
прочность образцов пряжи равна 280 сн.
![]() .
Определить долю образцов всей пряжи,
прочность которой отклоняется от средней
на величину не больше 20 сн. Считается,
что прочность приближенно изменяется
по нормальному закону.
.
Определить долю образцов всей пряжи,
прочность которой отклоняется от средней
на величину не больше 20 сн. Считается,
что прочность приближенно изменяется
по нормальному закону.
Здесь используем частный случай формулы Лапласа
![]() .
В рассматриваемом примере а =280,
.
В рассматриваемом примере а =280,
![]() .
Итак, имеем
.
Итак, имеем
![]() .
.
1. Локальная формула Муавра-Лапласа
Вернемся к биноминальному распределению. Производится n независимых испытаний, в каждом из которых событие А может появиться с постоянной вероятностью Р. Пусть случайная величина Х означает число появлений события А в n независимых испытаниях. Возможные значения таковы: 1,2,...,n; вероятности возможных значений вычисляются по формуле Бернулли
.
Приведем без вывода числовые характеристики биноминального распределения:
![]() .
.
Заметим,
что при большом числе повторных испытаний
n
формула Бернулли приводит к громоздким
вычислениям, т.е. в этом случае является
неприемлемой в практических приложениях.
Однако согласно следствию из теоремы
Ляпунова биноминальное распределение
при достаточно больших значениях n
является асимптотически нормальным,
т.е. приближенно можно считать нормальным
распределением. Далее используя плотность
распределения нормальной случайной
величины
,с
учетом
![]() нетрудно получить следующую приближенную
формулу
нетрудно получить следующую приближенную
формулу
![]() .
.
Введем в
рассмотрение функцию
![]() .
Она является четной. Причем
.
Она является четной. Причем
![]() .
Значения функции
.
Значения функции
![]() обычно определяют по таблице значений
этой функции. Последнюю приближенную
формулу перепишем в виде
обычно определяют по таблице значений
этой функции. Последнюю приближенную
формулу перепишем в виде
![]() .
.
Эта формула называется локальной формулой Муавра - Лапласа.
Замечание.
Заметим, что вероятность
![]() принимает максимальное значение при m
= np. При этом
принимает максимальное значение при m
= np. При этом
![]() .
.
Пример. Смесь состоит из хлопка и шерсти в пропорции 2:3. Определить вероятность того, что в случайном соединении из 120 волокон хлопковых волокон окажутся 30.
В нашем примере р = 0,4; q = 0,6; n =120; m =30. Поскольку число испытаний достаточно большое, поэтому целесообразно использовать локальную формулу Муавра-Лапласа. Сначала вычислим значение параметра t:
![]() .
.
Итак,
![]() .
.
