Кодовые слова заданной длины

Пусть алфавит , тогда множество различных двухбуквенных кодовых слов

,

а множество трехбуквенных кодов

.

Количество кодовых слов длины r в алфавите численностью n обозначается (читается «а из эн по эр»). Очевидно, что это количество зависит от численности алфавита и от длины слова.

Теорема. Количество кодовых слов длины r в алфавите V численностью n=n(V) равно r-степени числа n:

(5) .

 Слово образуется за r действий: 1) выбрать из алфавита букву на 1-е место в слове, 2) выбрать букву на 2-е место и т. д. Каждое действие независимо от варианта исполнения предыдущих действий выполняется n способами — всякий раз выбирается одна из n букв. Тогда по правилу умножения количество различных слов равно

. 

#. Найдем количество кодовых слов в алфавите V_B={0; 1} длиной r=8 символов. Это количество равно .

Кодовые слова данного типа называются, как известно, байтами.

Численность булеана Теорема. Численность булеана множества X равна двойке, возведенной в степень, равную численности множества X:

(6) .

 Каждое подмножество можно выразить индексным кодом — кодовым словом длины n(X), в котором k-й символ является индексом вхождения элемента x_k в данное подмножество. Индекс 1, если x_k принадлежит подмножеству; индекс 0, если нет. Так коду 000…0 соответствует пустое подмножество, коду 01010…0 — подмножество .

Очевидно взаимно однозначное соответствие подмножеств и индексных кодов, значит количество подмножеств равно количеству кодов длины n из алфавита {0; 1}. Таких кодов . Значит . 

Перестановки

Df. Перестановками называются различные кортежи, составляемые из всех элементов множества.

Расположить предметы в ряд можно по-разному. Поменяв местами любые два предмета в «очереди», мы получим новую перестановку. Так из множества {a; b} можно получить перестановки {(a; b); (b; a)}; из множества {; ; } — множество перестановок

{(; ; ), (; ; ), (; ; ), (; ; ), (; ; ), (; ; )}.

Количество различных перестановок зависит от числа переставляемых предметов. Количество перестановок n предметов обозначают P_n (читается: число перестановок n предметов).

Теорема. Число перестановок элементов множества равно факториалу его численности.

(7)

Напомним, что факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n: n!=123…n.

#. Составляется расписание уроков на понедельник в 8-а классе. Необходимо включить на этот день математику, литературу, географию, историю и физкультуру. Расписания суть перестановки этих пяти предметов. Число различных расписаний равно .

 Опишем алгоритм образования перестановки:

1)	выбор элемента из множества V на первое место	n
2)	выбор элемента из оставшихся на второе место	n–1
3)	выбор элемента из оставшихся на третье место	n–2
. . .	. . .	. . .
n)	выбор элемента последнего оставшегося на n-е место	1

В правое поле записывается для каждого действия количество способов выполнения. На каждое место выбирается элемент из оставшихся после отбора на предшествующие места. Ясно, что число способов заполнения каждого места в перестановке на единицу меньше, чем предыдущего. Последнее место может быть занято только одним способом.

Число способов заполнения каждого места не зависит от вариантов выбора предшествующих элементов. Поэтому, к подсчету перестановок применимо правило умножения:

.

Записав произведение в обратном порядке, получим формулу (7). 

Замечание. Пустое множество считается упорядоченным: нуль элементов можно упорядочить одним способом. Чтобы распространить формулу (7) на пустое множество принято считать 0!=1.

Df. Перестановками с повторениями называются различные кортежи элементов множества, содержащего классы тожественных элементов.

К этому понятию приводит задача составления анаграмм — перестановок букв в слове или предложении. Очевидно, что количество анаграмм слова «молоко» меньше P₆. В самом деле: поменяв местами две буквы «о», мы не получим новую анаграмму. Обозначим неизвестное пока число анаграмм этого слова (шесть букв, из которых три повторяются). Пронумеруем теперь буквы «о» о₁, о₂, о₃, чтобы они различались хотя бы номером. Переставляя в каждой анаграмме эти буквы, мы получим обычных перестановок шести элементов. Отсюда видно, что .

Можно сформулировать теорему о числе перестановок с повторениями.

Теорема. Число перестановок элементов множества с повторениями равно факториалу его численности, деленному на числа перестановок элементов в каждом классе.

(8) .

Df. Циклической перестановкой называется упорядоченное расположение элементов в замкнутую цепь (по кругу).

# Пять девочек танцуют в хороводе (см. рис. 1.).

В циклической перестановке определён порядок следования элементов, но неизвестен первый элемент. Так, если Аня и Катя поменяются местами, получается новая циклическая перестановка. Однако когда все девочки делают шаг в сторону, и каждая занимает место предшествующей девочки, новой циклической перестановки не образуется. Порядок следования девочек не изменяется.

Т

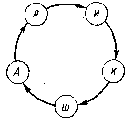Рис.1. Циклическая перестановка.

еорема. Число циклических перестановок элементов множества равно факториалу числа элементов без одного.

(9)

 Цепь из n звеньев можно разорвать n способами и получить n различных кортежей из каждой циклической перестановки (в этом можно убедиться на примере, показанном на рисунке 1 для n=5). Следовательно, численности циклических и обычных перестановок связаны соотношением: . Отсюда получаем формулу (9). 