12.4. Вимушені коливання

Рівняння вимушених коливань у контурі, що виникають внаслідок дії періодичного джерела струму має вид

(1)

з частинним розв'язком

, (2)

де .

Амплітуда коливань знаходиться стандартним розв'язком рівняння (1) і дорівнює

. (3)

Після підстановки характеристик елементів контуру одержимо

= . (4)

В (4) позначено реактивний опір на індуктивності та реактивний опір на конденсаторі, які ми визначимо нижче. Початкова фаза визначається так

. (5)

Загальний розв’язок рівняння вимушених коливань є сумою загального розв'язку однорідного рівняння (рівняння вільних згасаючих коливань) та знайденого частинного розв'язку. З часом загальний розв’язок однорідного рівняння згасне (е^-t0) й установляться коливання, що задаються частинним розв'язком.

Струм у контурі має величину

, (6)

де

І_о= , Z= . (7)

Величина Z називається імпедансом і є повним опором струмові у RLC-контурі. Для зручності подальших викладок фазових співвідношень приймемо початкову фазу струму у вигляді

або

. (8)

Тепер струм у колі запишеться у вигляді

, (9)

а заряд

. (10)

Напруга на опорі R становить

(11)

Напруга на індуктивності L. Запишемо вираз (п.2) у вигляді

(12)

де

є напруга на індуктивності з амплітудою

. (13)

Величина

(14)

має розмірність опору і називається реактивним опором індуктивності. Напруга на індуктивності випереджає напругу на опорі R за фазою на /2.

Напруга на конденсаторі C

.

,

= U_oC cos(t - -/2), (15)

де

(16)

є амплітуда напруги на конденсаторі. Величина

(17)

м ає розмірність опору і називається реактивним опором конденсатора. Напруга на конденсаторі U_C запізнюється відносно напруги на омічному опорі U_R за фазою на /2.

Фазові співвідношення між можна представити на фазовій (комплексній) площині за допомогою відповідних векторів, як це показано на Мал.134 із відповідними зсувами за фазою.

Резонанс напруги. Напруга та заряд на конденсаторі є функцією зовнішньої частоти . Положення екстремуму задається резонансною частотою

(18)

і визначає їх максимальне значення. Для малих R коли, , резонансну частоту можна покласти рівною _o, і

. (19)

В одержаному виразі Q - є добротність контуру і вона показує у скільки разів напруга на конденсаторі при резонансі може перевищити прикладену напругу .

Резонанс струму. Максимальне значення струму в контурі задається мінімальним значенням імпедансу Z, яке визначається умовою , тобто

. (20)

При цьому резонансна частота становить

. (21)

При резонансі струму його амплітуда буде максимальною

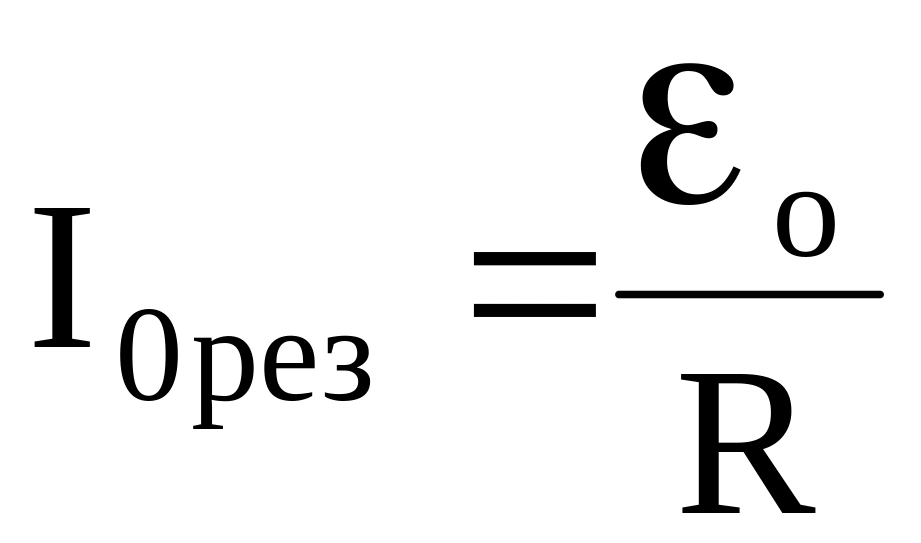. (22)

Приклад 1. В контурі діє змушуюче джерело змінного струму з частотою і напругою . Резонанс струму спостерігається при ємності конденсатора , причому . Обчислити індуктивність контуру та омічний опір.

Дано: , =50 Гц, , , L-?, R-?

Розв’язок