2.1.2. Реализация булевых функций формулами

Для задания булевых функций помимо таблиц также используют формулы. Формулы обычно строят по «принципу матрешек», вкладывая друг в друга символические записи элементарных функций. Говоря о формуле, часто указывают, с использованием каких функций она строилась. Например, - это формула над множеством, состоящим из дизъюнкции, импликации и штриха Шеффера, а - формула над множеством, состоящим из конъюнкции, отрицания и эквивалентности.

Каждой формуле сопоставляется функция (при этом говорят, что формула реализует функцию). Процедура сопоставления пошаговая. Покажем, как действовать, на примерах.

Упражнение 2.9. Построить таблицу истинности и выписать вектор значений функции:

а) ; б) ; в) .

◄ а)

0	0	1	0	1
0	1	1	1	0
1	0	0	0	0
1	1	0	0	0

Вектор значений функции .

0	0	0	0	1	1
0	0	1	0	1	1
0	1	0	1	1	1
0	1	1	1	1	1
1	0	0	1	0	0
1	0	1	1	1	1
1	1	0	1	1	1
1	1	1	1	1	1

б)

Вектор значений функции .

в) решить самостоятельно.►

Итак, на примерах мы рассмотрели понятие формулы над множеством функций и понятие функции, реализуемой формулой над . Теперь этим понятиям нужно дать формальные определения.

Определение. Пусть - некоторое подмножество функций из ; - множество символов, используемых для обозначения функций из множества ; - множество символов, используемых для обозначения переменных; , . Тогда

1. каждое выражение вида 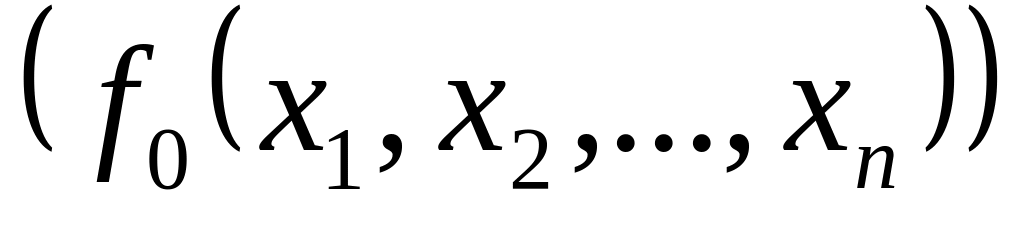, называется формулой над ;

2. выражение вида 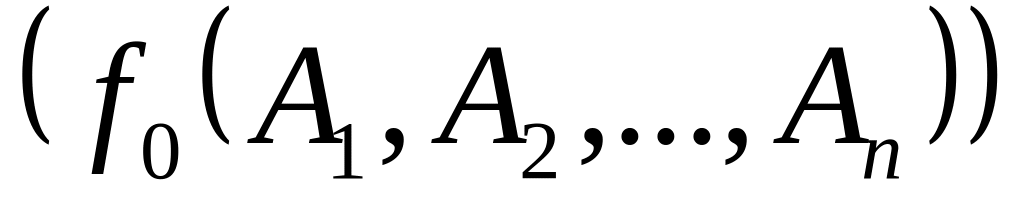, где - либо символ переменной 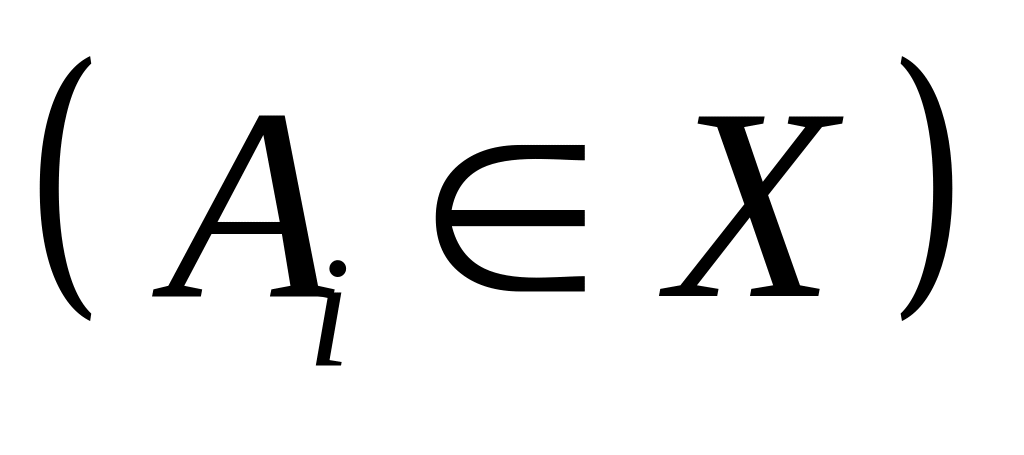, либо формула над , называется формулой над .

Обозначения: - формула над множеством функций ; - формула над множеством функций .

Определение функции, реализуемой формулой, также строится индуктивно. Оно громоздкое и довольно сложное для восприятия. Мы рассмотрим его несколько позже. Опыт показывает, что при первом знакомстве с курсом вполне достаточно понимать, что такое функция, реализуемая формулой, интуитивно.

Если формула реализует функцию , то пишут .

Функцию , реализуемую формулой над множеством функций , будем называть суперпозицией функций .

Замечание. Для упрощения записи формул введен ряд соглашений:

а) внешние скобки у формул можно опускать;

б) вместо можно писать , а вместо – или ;

в) связку « » принято считать сильнее любой двуместной связки, поэтому внешние скобки в выражении, над которым стоит знак « – », можно опускать;

г) связку « » принято считать сильнее любой другой двуместной связки, поэтому в скобки выражения , , можно не брать.

Например, формулу можно записать в виде .

Упражнение 2.10. Показать, что формулы реализуют равные функции:

а) и ; б) и .

◄ а)

0	0	1	0	1	1
0	1	1	0	1	1
1	0	0	0	0	0
1	1	0	1	1	1

б) Выполнить самостоятельно. ►

Если две формулы и реализуют равные функции, то их называют равносильными и пишут .

Теорема. Для формул над множеством имеют место следующие равносильности:

1. ; 2. ;

3. ; 2. ;

5. ; 6. ;

7. ; 8. ;

9. ; 10. ;

11. ; 12. ;

13. ; 12. ;

15. ; 16. ;

17. ; 18. ;

19. .

◄ Чтобы доказать справедливость любого из этих равенств, нужно убедиться в равенстве функций, реализуемых формулами, записанными в его левой и правой частях. Для этого достаточно построить таблицы истинности этих функций. Например, для равносильности под номером 10 имеем:

0	0	0	1
0	1	0	1
1	0	0	1
1	1	1	0
0	0	1	1	1
0	1	1	0	1
1	0	0	1	1
1	1	0	0	0

Как видим, формулы и реализуют равные функции и, следовательно, равносильны.

Справедливость остальных равенств проверьте самостоятельно. ►

Равносильности 1-19 характеризуют свойства дизъюнкции, конъюнкции и отрицания: 1 и 2 – коммутативность, 3 и 4 – ассоциативность, 5 – дистрибутивность конъюнкции относительно дизъюнкции, 6 – дистрибутивность дизъюнкции относительно конъюнкции, 7 и 8 – идемпотентность. Равносильности 9 и 10 называют законами де Моргана, 15 и 16 – законами поглощения, 17 – законом противоречия, 18 – законом исключенного третьего, 19 – законом двойного отрицания.

Дополним соглашение об упрощенной записи формул: в случае многократного применения ассоциативной операции скобки можно опускать. Например, формулу можно записать в виде . В дальнейшем будем также употреблять следующие обозначения: и .

Упражнение 2.11. Учитывая соглашения о порядке выполнения операций, опустить «лишние» скобки и знак « » в формулах:

а) ; б) .

◄ а) ;

б) выполнить самостоятельно. ►

Упражнение 2.12. Доказать, что имеет место равносильность:

а) ; б) ;

в) ; г) ;

д) ; е) .

◄ Выполнить самостоятельно. ►

Упражнение 2.13. Применяя равносильные преобразования, упростить формулу:

а) ; б) ; в) ; г) .

◄ а) .

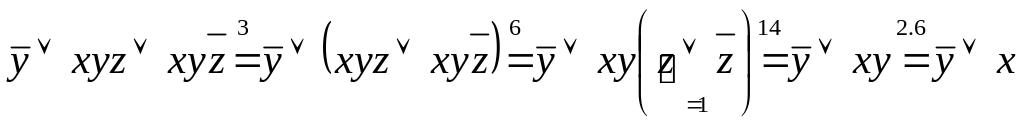б) .

в) и г) выполнить самостоятельно. ►

Упражнение 2.12. Указать существенные и фиктивные переменные функции:

а) ;

б) .

◄ а) Преобразуем формулу, используя равносильность :

.

Поскольку на любом наборе и на любом наборе , то согласно определению , - фиктивные переменные. Переменная же - существенная, т.к. , .

б) выполнить самостоятельно. ►

Обратите внимание. Если функция реализована формулой, в которую некоторая переменная не входит, то эта переменная фиктивная. Обратное утверждение неверно. Действительно, в упражнении 14 а) мы рассмотрели функцию, реализованную формулой, содержащую переменные , , однако эти переменные оказались фиктивными.

Упражнение 2.15. Выяснить, на скольких векторах 4-х мерного булева куба обращается в ноль функция: а) ; б) .

◄ а) Функция обращается в ноль, если или . Равенства выполняются, только если все переменные равны единице. Равенства выполняются на таких наборах значений переменных , у которых одновременно не равны единице и одновременно не равны единице. При построении конкретного булевого вектора , отвечающего этим требованиям, будем сначала выбирать пару , а затем пару . Каждую из этих пар можно выбрать тремя способами (взять 0,0, или 0,1, или 1,0). Значит, согласно правилу произведения построить булев вектор, на котором оба слагаемых и равны нулю, можно девятью способами.

Таким образом, есть десять векторов, на которых функция обращается в нуль.

б) решить самостоятельно. ►