Московский государственный институт электронной техники
(технический университет)
А. И. Литвинов
МЕТОДИЧЕСКОЕ ПОСОБИЕ
к практическим занятиям по «Дифференциальным уравнениям»
Утверждено методическим советом каф. ВМ-2
Зав. кафедры С. Г. Кальней
МИЭТ, 2012 г.
————————————————————————————————————————
Прочти, реши и опять прочти!..
Настоящее методическое пособие предназначено помочь студентам в освоении теоретических вопросов предмета «Дифференциальные уравнения» путём использования подробно решённых задач и примеров.
Одновременно, пособие должно помочь наиболее мотивированным студентам развивать навыки самостоятельной работы, что очень важно при подготовке инженера любой специальности.
Тем, кто захочет воспользоваться возможностью показать себя постоянно и эффективно работающим, привлечь к себе внимание преподавателей и научных руководителей, приобрести авторитет среди своих товарищей, пособие тоже окажет помощь.
Рассмотренные и доступные с самого начала семестра материалы помогут качественно готовиться и к лекциям, и практическим занятиям, и к различным контрольным испытаниям.
СОДЕРЖАНИЕ:
№ |
Тема занятия: |
Стр. |
1. |
Основные понятия. Теорема о существовании и единственности решения ДУ 1-го порядка. Уравнение 1-го порядка с разделяющимися переменными. |
2 |
2. |
Уравнения первого порядка с разделяющимися переменными. Систематизация и закрепление знаний. |
8 |
3. |
Однородные функции и однородные уравнения первого порядка. Уравнения специального вида, приводящиеся к однородному уравнению 1-го порядка. Выдача части-1 БДЗ. |
11 |
4. |
Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли. |
17 |
5. |
Уравнения в полных дифференциалах. |
24 |
6. |
Уравнения 1-го порядка, не разрешённые относительно производной. |
30 |
7. |
Повторение: все типы уравнений 1-го порядка. Обзорные упражнения: определение типа дифференциального уравнения и обсуждение общего алгоритма решения. Систематизация знаний. Подготовка к контрольной работе. |
36 |
8. |
Уравнения 1-го порядка. Контрольная работа №1. Приём части-1 БДЗ. Выдача части-2 БДЗ. |
36 |
9. |
Уравнения высших порядков. Уравнения, допускающие понижение порядка. |
11 |
10. |
Линейные ДУ n-го порядка. Линейная зависимость решений линейного уравнения. Линейное однородное уравнение. |
11 |
11. |
Линейные неоднородные уравнения с постоянными коэффициентами. Решение методами: «вариации произвольных постоянных» и «неопределенных множителей». |
11 |
12. |
Краевые задачи для линейных дифференциальных уравнений. Повторение: решение линейных ДУ 2-го и 3-го порядков. Систематизация знаний. Подготовка к контрольной работе. |
11 |
13. |
Уравнения n-го порядка. Контрольная работа №2. Прием части-2 БДЗ. Выдача части-3 БДЗ. |
11 |
14. |
Системы дифференциальных уравнений первого порядка. Сведение системы ДУ к одному уравнению высшего порядка. |
11 |
15. |
Системы линейных однородных дифференциальных уравнений 1-го порядка с постоянными коэффициентами: общее и частное решения. |
11 |
16. |
Системы линейных неоднородных дифференциальных уравнений 1-го порядка с постоянными коэффициентами. Правая часть: специальная и произвольная. Самостоятельная работа – 40 мин. Приём части-3 БДЗ. |
11 |
17. |
Повторение и систематизация материала. Подготовка к экзамену. |
11 |
•◄●►•
Замечание: если в рассматриваемом Задании пример имеет номер 3-9, это значит, что цифра 3 указывает порядковый номер примера в этом Задании, а цифра 9 указывает номер примера из Задачника, указанного в Семестровом плане студентов.
ЗАНЯТИЕ 1. Основные понятия. Теорема существования и единственности ДУ 1-го порядка. Уравнения первого порядка с разделяющимися переменными.
☺ ☻ ☺
Основные понятия:
1. Дифференциальным уравнением (ду) называют равенство, содержащее независимые переменные, искомую функцию и её производные (или дифференциалы).
2. Решить ду – значит найти все его решения!
3. Решение ду – любая функция, которая, будучи подставлена в исходную запись уравнение, обращает его в тождество!
••• ≡ •••
Пример
1–1:
Показать, что при любом действительном
значении параметра
заданная функция
является решением ДУ:
. (1)
Решение:
1).
Разделим уравнение на
.
Получаем уравнение в виде:
. (2)
2).
Для нахождения производной заданной
функции вспомним:
,
так как имеем:
-
табличный интеграл!
Тогда:
=
.
3).
Подставим заданную функцию
и ее производную
в уравнение (2), которое равносильно
исходному уравнению (1): 
→ тождество.
4). Это значит, что заданная функция является решением заданного уравнения.
Ответ: заданная функция является решением заданного уравнения.
Пример
2–4:
В заданном семействе:
выделить уравнение кривой, удовлетворяющей
приведенному начальному условию:
.
Решение:
1).
Выделить из семейства кривых кривую,
которая проходит через точку (0,1) – это
значит вычислить значение произвольной
постоянной
,
при условии, что
=0,
=1.
2).
Подставим
=0,
=1
в выражение семейства:
,
откуда
=1.
3).
Тогда уравнение кривой семейства,
проходящей через точку (0,1):
.
Ответ: уравнение кривой: .
Пример
3–9:
Составить дифференциальное уравнение
семейства парабол:
. (1)
Решение:
1).
Преобразуем выражение семейства
(известная операция выделения полного
квадрата):
.
При непрерывном изменении параметра
ось параболы
смещается влево при значении параметра
,
вправо при значении
;
одновременно вершина параболы движется
по параболе
.
2).
Вычислим производную
для заданного семейства:
.
(2)
3). Для получения дифференциального уравнения нужно исключить параметр из выражения (1) или из выражения (2):
а)
умножив выражение (2) на
,
получим уравнение
=[учтём
(1)]
=
;
б)
получено дифференциальное уравнение:
=
.
Ответ: ДУ для семейства парабол = .
Пример
4–16:
Методом изоклин построить приближенно
семейство интегральных кривых для
дифференциального уравнения:
.
Р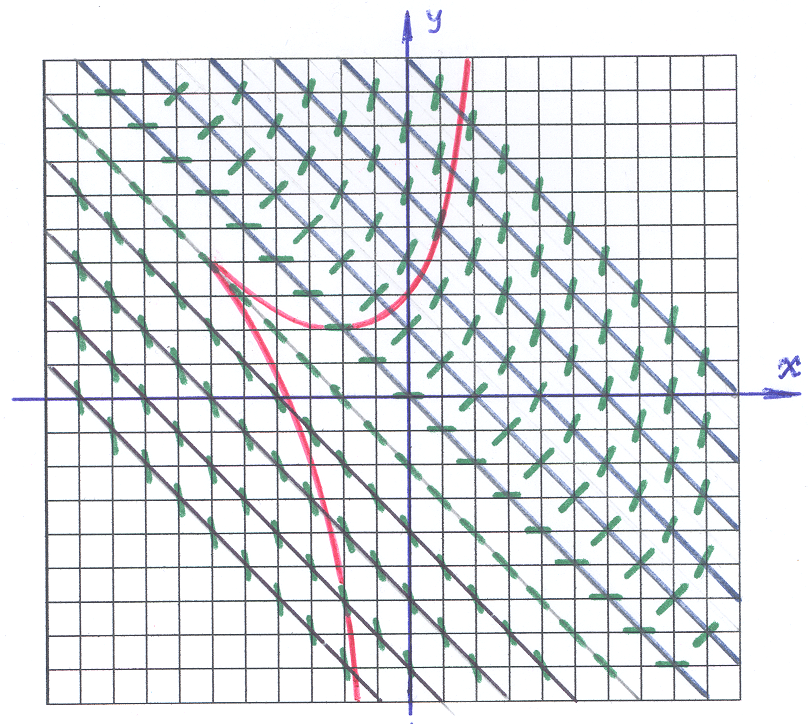
ешение:
1).
Уравнение изоклин для заданного
дифференциального уравнения получается
из исходного уравнения приравниванием
=
.
В нашем случае каждая изоклина – это
прямая:
=
.
На рисунке изоклины выделены «синим»
цветом. На каждой изоклине черточка
(«зеленая») отражает конкретное
значение
,
определяющее изоклину, то есть: на
каждой изоклине наклон черточки один
и тот же.
2). Черточки играют роль «железных опилок» в опытах по физике: они показывают направление «поля». Возникает «зрительный образ», который определяет «присутствие некоторой кривой», касательные к которой мы и видим. Это и есть приближенно выделяемая «интегральная кривая» (одна из них выделена «красным» цветом), то есть «решение» заданного ДУ.
Ответ: интегральная кривая представлена на рисунке.
Пример
5–26:
Решить дифференциальное уравнение:
. (1)
Решение:
1).
Прежде всего, отметим, что исходное
уравнение (1) не может иметь решения в
виде
,
в частности в виде функции
.
Это значит, что дифференциал
не может быть равным 0. В то же время,
функция
=0
есть решение уравнения (1).
2).
Умножим исходное уравнение (1) на
дифференциал
.
Уравнение (1) перепишем в дифференциальной
форме: 
.
(2)
3).
Нетрудно заметить, что уравнение (2) есть
уравнение с разделяющимися переменными.
Так как решение
уже учтено, теперь примем, что
и перепишем уравнение (2) в виде: 
+
=0. (3)
4). Используя простейшие приёмы вычисления неопределённых интегралов, проинтегрируем уравнение (3). При получении общего решения уравнения (3) применим два принципиально разных способа использования произвольной постоянной величины:
→
или
.
(4)
→
или
.
(5)
Замечания: 1. При получении выражений (4) и (5) принципиальным было применение условия y≠0. При получении записи (5) также необходимо потребовать выполнения условия C≠0!..
2. Использование записи (5) удобнее в случае решения задачи Коши: вычисление постоянной C совсем просто, при использовании (4) пришлось бы применять логарифмы!.. Если общее решение уравнения воспринимать как совокупность кривых, то записи эквиваленты!..
Ответ:
общее решение ДУ
;
хотя при получении общего решения
произвольная постоянная величина
не должна принимать значение 0, формально
из него можно получить решение исходного
уравнения
при значении
.
Пример
6–31:
Решить дифференциальное уравнение:
. (1)
Решение:
1).
Прежде всего, отметим, что исходное
уравнение (1) имеет решения в виде функций:
– прямые, параллельные оси
,
и
,
то есть ось
.
2).
Теперь воспользуемся тем, что переменные
в уравнении разделяются. Так как решения
и
учтены, примем теперь
и
,
и запишем уравнение в виде:
. (2)
3). Используя простейшие приёмы вычисления неопределённых интегралов, проинтегрируем уравнение (2). Получаем общее решение уравнения (2):
→
.
(3)
Ответ: общее решение ДУ ; в данном случае решение исходного уравнения можно получать из общего при значении =0; решения также формально можно получать из общего решения.
Пример
7–41:
Решить дифференциальное уравнение:
. (1)
Решение:
1).
Преобразуем заданное уравнение к виду:
=
.
Известно, что такое уравнение легко
приводится к уравнению с разделяющимися
переменными!
2).
Примем
и вычислим производную
,
то есть
.
В нашем случае получаем
,
что есть уравнение с разделяющимися
переменными!
3).
Уравнение
имеет решение в виде функции:
.
Учитывая обозначение
,
запишем решение
– прямая линия.
Замечание: Увидеть решение непосредственно из исходного уравнения было бы совсем непросто!
4).
Пусть теперь
.
Запишем уравнение
в виде:
,
или (для удобства!) в виде:
. (2)
5).
Интегрирование уравнения (2) не составит
труда, даже на начальном этапе освоения
неопределённого интеграла 
→
. (3)
Ответ:
общее решение ДУ
;
в данном случае решение
можно получить формально из общего при
значении
=0;
запишем общее решение и в виде
,
из которого решение
получается из общего при значении
=0.
Пример
8–43:
Решить дифференциальное уравнение:
,
. (1)
Решение:
1).
Прежде всего, отметим, что исходное
уравнение (1) имеет решение:
–
ось
.
2).
Переменные в уравнении разделяются.
Так как решение
уже учтено, примем теперь
,
и запишем уравнение в виде: 
. (2)
3).
Интегрирование уравнения (2) не составит
труда, даже на начальном этапе освоения
неопределённого интеграла 
→
. (3)
4).
Используя начальные условия
,
вычисляем:
и получаем
частное решение уравнения:
–
гипербола, её график включает две
ветви. Начальные условия выделяют правую
ветвь гиперболы!
Ответ: – частное решение ДУ: правая ветвь гиперболы.
Пример
16–167:
Найти уравнение кривой линии, проходящей
через точку
,
если длина отрезка полуоси абсцисс,
отсекаемого её касательной, равна
квадрату абсциссы точки касания.
Решение:
В
Примере
1–19
Главы 1 пособия получено выражения:
OT=
– длина отрезка полуоси абсцисс,
отсекаемого её касательной; абсциссу
точки касания обозначим D=
.
С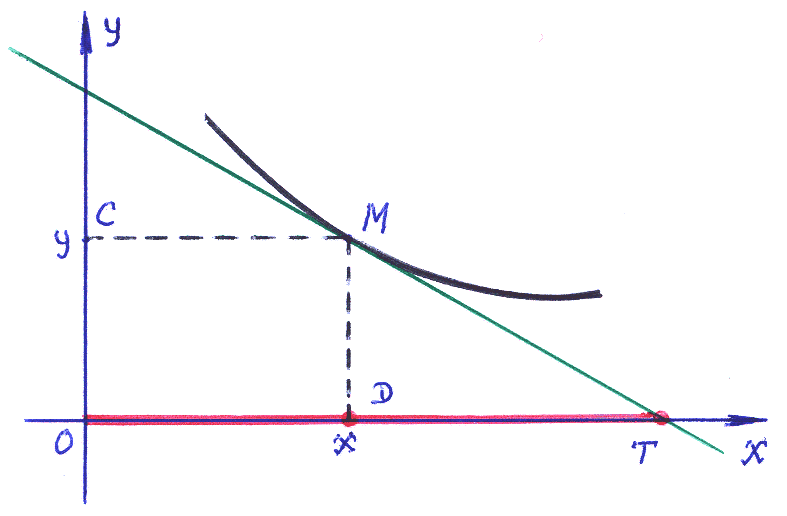
огласно
условию задачи и в соответствии с
принятыми обозначениями необходимо
рассмотреть два случая:
▪ Случай-1:
; (1)
▪ Случай-2:
. (2)
Случай-1.
1).
Запишем дифференциальное уравнение
(1) в виде:
– уравнение с разделяющимися переменными,
обозначим его
.
2).
Из записи
нетрудно выделить решения:
–
ось
,
–
прямая, параллельная оси
и
–
ось
.
Эти решения не отражают существа
поставленной геометрической
задачи.
3).
Пусть теперь
и
.
Перепишем уравнение
в виде
=
–
переменные разделились. Интегрируем
уравнение:
–
=
=
.
Используя табличные интегралы и исключая
логарифмы, можем записать общее решение:
=
,
или
=
. (3)
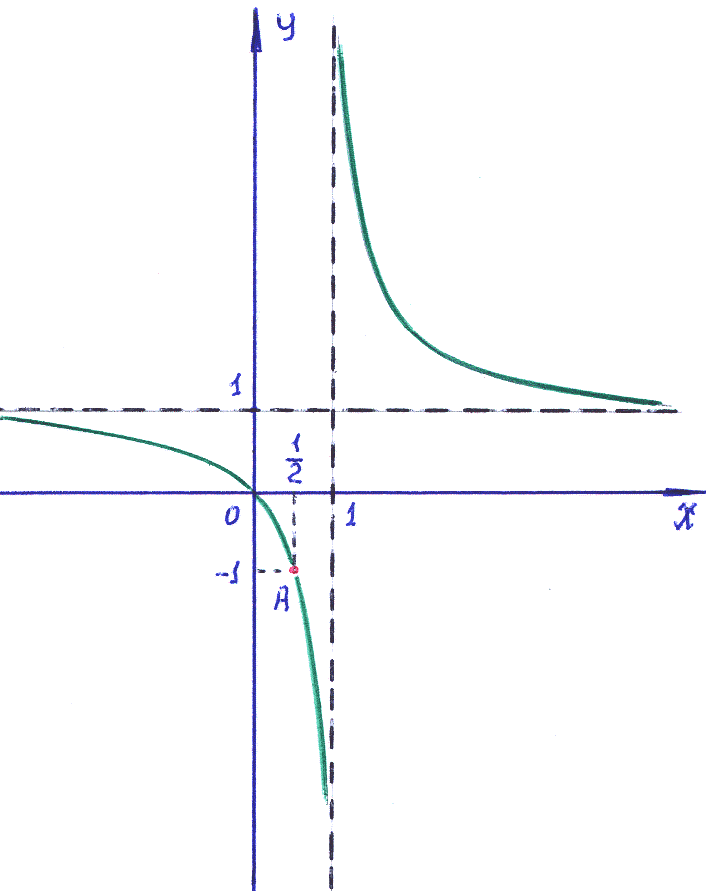
4). Из записи общего решение дифференциального уравнения следует, что это семейство гипербол.
Для
иллюстрации присвоим произвольной
величине
значение 1. Известно, что график функции
=
может быть получен, если к простейшей
гиперболе
применить преобразования:
Сместить график вправо на 1, лучше сместить ось на 1 влево.
Сместить график вверх на 1, лучше сместить ось на 1 вниз.
Учёт параметра в записи (3) может быть отмечен возможными действиями: сжатие-растяжение вдоль оси , вращение вокруг оси и движение вверх-вниз.
Так
как по условию задачи кривая должна
проходить через точку
,
то используя выражение общего решения
(3), получаем значение
.
Именно для этого случая применён рисунок.
Учитывая условие задачи, заметим, что
решением является ветвь гиперболы,
проходящая через точку
.
Случай-2.
1).
Запишем дифференциальное уравнение
(2) в виде:
– уравнение с разделяющимися переменными,
обозначим его
.
2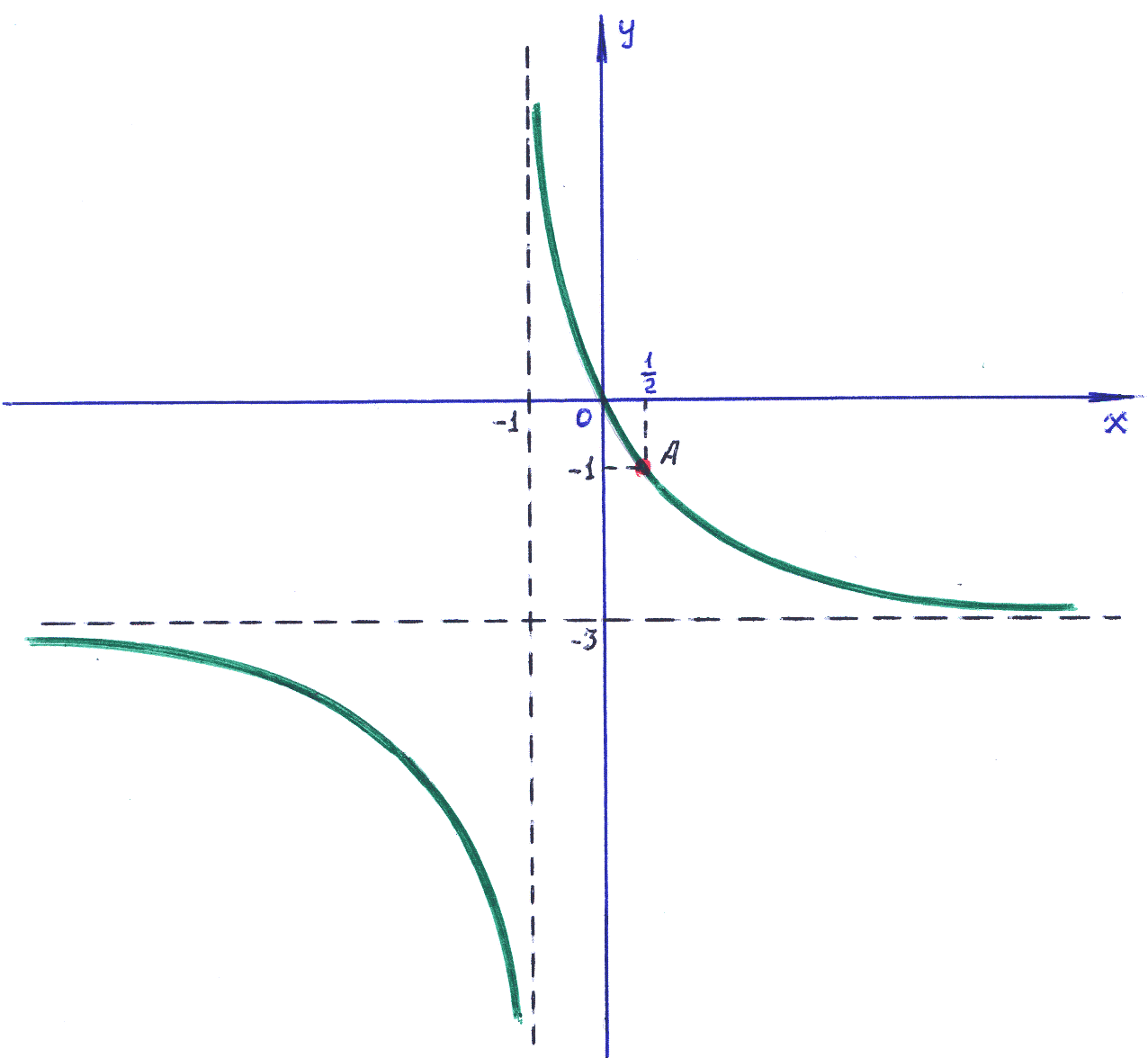
).
Из записи
нетрудно выделить решения:
–
ось
,
–
прямая, параллельная оси
и
–
ось
.
Эти решения не отражают существа
поставленной геометрической
задачи.
3).
Пусть теперь
и
.
Перепишем уравнение
в виде
=
–
переменные разделились. Интегрируем
уравнение:
–
=
=
.
Используя табличные интегралы и исключая
логарифмы, можем записать общее решение:
=
,
или
=
. (4)
4). Из записи общего решение дифференциального уравнения следует, что это семейство гипербол.
Для
иллюстрации присвоим произвольной
величине
значение –3.
Известно, что график функции
=
может быть получен, если к простейшей
гиперболе
применить преобразования:
Сместить график влево на 1, лучше сместить ось на 1 вправо.
Сместить график вниз на 3, лучше сместить ось на 3 вверх.
Учёт параметра в записи (4) может быть отмечен возможными действиями: сжатие-растяжение вдоль оси , вращение вокруг оси и движение вверх-вниз.
Так
как по условию задачи кривая должна
проходить через точку
,
то используя выражение общего решения
(4), получаем значение
.
Именно для этого случая применён рисунок.
Учитывая условие задачи, заметим, что
решением является ветвь гиперболы,
проходящая через точку
.
Ответ: Случай-1: = – общее решение и частное: = .
Случай-2:
=
–
общее решение и частное:
=
.
☻
Вопросы для самопроверки:
Какое уравнение называют дифференциальным?
Как определить порядок ДУ?
Что значит - решить дифференциальное уравнение?
Что такое решение ДУ, частное решение ДУ?
Что такое общее решение ДУ?
Что значит решить Задачу Коши?
Что такое семейство кривых?
Как построить уравнение, решением которого является заданное семейство кривых?
Каковы стандартные формы ДУ с разделяющимися переменными и их решение?
Задачи для самоподготовки:
Пример
C1–1:
В заданном семействе:
выделить уравнение кривой, удовлетворяющей
приведенному начальному условию:
.
Ответ:
.
Пример
C1–2: Решить
дифференциальное уравнение:
.
Ответ:
.
Пример
C1–3: Решить
дифференциальное уравнение:
.
Ответ:
.
Пример
C1–4: Решить
дифференциальное уравнение:
.
Ответ:
.
Пример
C1–5: Решить
дифференциальное уравнение:
.
Ответ:
.
Пример C1–6: Найти уравнение кривой, проходящей через точку (1,2), если её подкасательная вдвое больше абсциссы точки касания.
Ответ:
и
.
< * * * * * >
ЗАНЯТИЕ 2. Уравнения первого порядка с разделяющимися переменными. Систематизация и закрепление знаний.
☺ ☻ ☺
Замечание: При выполнении Задания необходимо руководствоваться основными понятиями, представленными в начале Занятия 1.
••• ≡ •••
Пример
1–3:
Показать, что при любом действительном
значении параметра
заданная функция
является решением ДУ:
. (1)
Решение:
1).
Разделим уравнение (1) на
:
. (2)
2).
При нахождении производной заданной
функции учтем, что функция
в нашем примере задана неявно.
Дифференцируем заданную функцию по x;
учитывая
:
=[учтём,
что
]=
. (3)
Применяя
тождественные преобразования (3), получим:
. (4)
3). Подставив в уравнение (2) левую часть равенства (4), получаем очевидное тождество:
4).
Это значит, что заданная (неявная) функция
является решением уравнения (1).
Ответ: заданная функция является решением заданного уравнения.
Пример
2–6:
В заданном семействе
выделить уравнение кривой, удовлетворяющей
приведенному начальному условию:
=
–1.
Решение:
1).
Выделить из семейства кривых кривую,
которая проходит через точку
– это значит вычислить значение
,
при условии, что
=0,
=
–1.
2).
Подставим
=0,
=
–1 в выражение семейства:
,
откуда
=
–3.
3). Тогда уравнение кривой семейства, проходящей через точку (0,1): .
3).
Запишем выражение кривой семейства,
проходящей через точку
:
.
Ответ: уравнение кривой: .
Пример
3–17:
Методом изоклин построить приближенно
семейство интегральных кривых для
дифференциального уравнения:
.
Р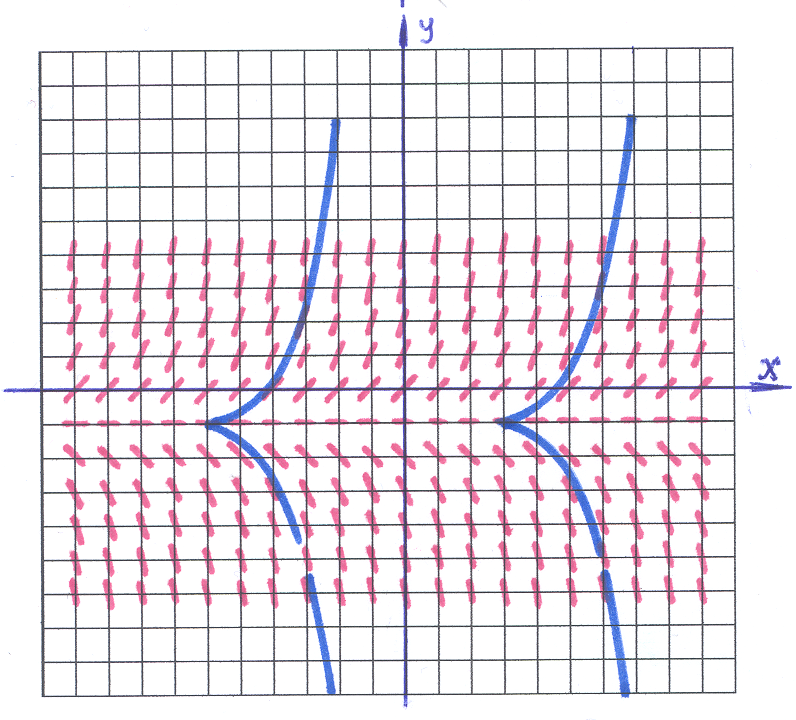
ешение:
1).
Уравнение изоклин для заданного
дифференциального уравнения получается
из исходного уравнения приравниванием
=
.
У нас каждая изоклина – прямая:
=
.
На рисунке изоклины выделены «серым»
цветом: прямые, параллельные оси ОХ. На
каждой изоклине черточка («красная»)
отражает конкретное значение
,
определяющее изоклину, то есть: на каждой
изоклине наклон черточки один и тот же.
2). Черточки играют роль «железных опилок» в опытах по физике: они показывают направление «поля». Возникает «зрительный образ», который определяет «присутствие некоторой кривой», касательные к которой мы и видим. Это и есть приближенно выделяемая «интегральная кривая» (одна из них выделена «синим» цветом), то есть «решение» заданного ДУ.
Ответ: интегральная кривая представлена на рисунке.
Пример
4–23:
Решить дифференциальное уравнение:
.
Решение:
1).
Умножив исходное уравнение на дифференциал
,
можем записать:
.
Нетрудно заметить, что это
уравнение с разделяющимися переменными.
2). Отметим, что из исходной записи уравнения ни одного решения не следует.
3).
Интегрируем уравнение:
=
.
Используя табличные интегралы, нетрудно
записать общее решение в виде:
=
x–
+C,
или в виде:
.
Ответ: – общее решение ДУ.
Пример
5–25:
Решить дифференциальное уравнение:
. (1)
Решение:
1). Прежде всего, отметим, что исходное уравнение (1) имеет очевидное решение =0.
2).
Умножим исходное уравнение (1) на
дифференциал
.
Уравнение (1) перепишем в дифференциальной
форме: 
.
(2)
3). Нетрудно заметить, что уравнение (2) есть уравнение с разделяющимися переменными. Так как решение уже учтено, теперь примем, что и перепишем уравнение (2):
=2
. (3)
4).
Интегрируем (3):
=2
или
→
.
–
общее решение дифференциального
уравнения.
Ответ: общее решение ДУ ; хотя при получении общего решения произвольная постоянная величина не должна принимать значение 0, формально из него можно получить решение исходного уравнения при значении .
Пример
6–30:
Решить дифференциальное уравнение:
. (1)
Решение:
1).
Прежде всего, отметим, что исходное
уравнение (1) не предлагает простейших
решений вида:
и
.
2).
Запишем уравнение (1) в виде: 2
+2
=0.
Умножение
на число 2 учитывает, что
!
3).
В результате интегрирования получим:
–
общее решение ДУ.
Ответ: общее решение ДУ: .
Пример
7–38:
Решить дифференциальное уравнение:
=
. (1)
Решение:
1). Прежде всего, отметим, что исходное уравнение (1) не предлагает простейших решений вида: и . Также легко заметить, что уравнение (1) равносильно уравнению:
=
. (2)
2).
Примем
и вычислим производную
,
то есть
.
В нашем случае получаем
,
что есть уравнение с разделяющимися
переменными!
3).
Уравнение
имеет решение в виде функции:
.
Учитывая обозначение
,
запишем решение
– прямая линия.
Замечание: Увидеть решение непосредственно из исходного уравнения было бы совсем непросто!
4).
Пусть теперь
.
Запишем уравнение
в виде:
,
или (для удобства!) в виде:
. (3)
5).
Интегрирование уравнения (3) не составит
труда, даже на начальном этапе освоения
неопределённого интеграла 
→
. (4)
Ответ:
общее решение ДУ
;
в данном случае решение
можно получить формально из общего при
значении
=0;
запишем общее решение и в виде
,
из которого решение
получается из общего при значении
=0.
☻
Вопросы для самопроверки:
Какое уравнение называют дифференциальным?
Как определить порядок ДУ?
Что такое решение ДУ, частное решение ДУ?
Что такое общее решение ДУ?
Что значит решить Задачу Коши?
Что такое семейство кривых?
Как построить уравнение, решением которого является заданное семейство кривых?
Каковы стандартные формы ДУ с разделяющимися переменными?
Какова стандартная схема решения ДУ с разделяющимися переменными?
Задачи для самоподготовки:
Пример
C2–1:
Показать, что при любом действительном
значении параметра
заданная функция
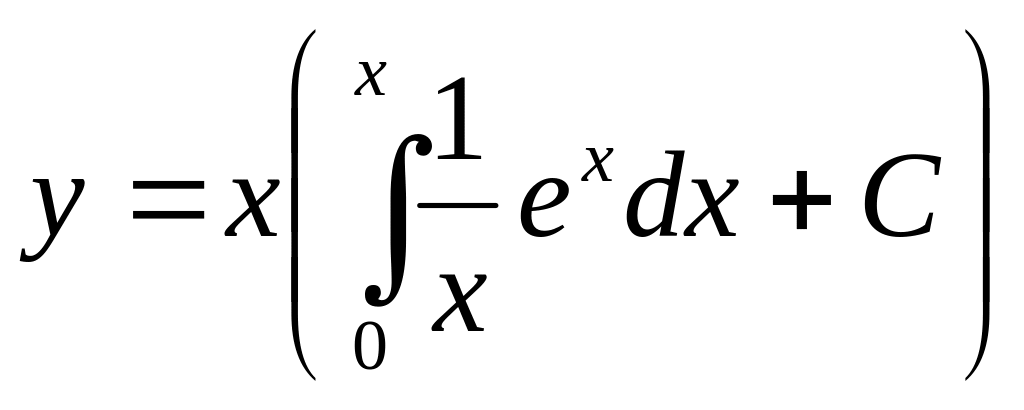является решением ДУ:
.
Ответ: заданная функция является решением ДУ.
Пример
C2–2: Составить
дифференциальное уравнение семейства
гипербол:
.
Ответ:
.
Пример
C2–3: Методом
изоклин построить приближенно семейство
интегральных кривых для дифференциального
уравнения:
=
–
.
Ответ: рисунок семейства прилагается.
Пример
C2–4: Решить
дифференциальное уравнение:
=
.
Ответ:
– общее решение ДУ (семейство гипербол).
Пример
C2–5: Решить
дифференциальное уравнение:
.
Ответ:
–
общее решение ДУ.
Пример
C2–6: Найти
частное решение ДУ:
,
удовлетворяющее условию:
=1.
Ответ:
– частное решение ДУ.
Через точку
проходит единственная кривая.
< * * * * * >
ЗАНЯТИЕ 3. Однородные функции и однородные уравнения первого порядка. Уравнения специального вида, приводящиеся к однородному дифференциальному уравнению 1-го порядка. Выдача части-1 БДЗ.
☺ ☻ ☺
Однородные функции и их использование в решениях однородных ДУ 1-порядка:
1.
Функция
называется
однородной функцией порядка
относительно
переменных
,
если при любом
верно:
.
В частном случае функция может оказаться
такой, что
.
В этом случае, так как
=1,
говорят, что функция
однородная нулевого порядка. Однородную
функцию нулевого порядка можно представить
в виде функции:
=
.
Если
функция
однородная
функция порядка
относительно
переменных
,
то её отношение к величине
есть однородная функция нулевого
порядка. В таком случае верно:
=
,
что равносильно записи исходного
определения:
.
Однородные
дифференциальные уравнения 1-порядка
вида:
. (1)
1). Запись (1)
подсказывает, что исследуемый процесс
определяется отношением величин
и это отношение неплохо бы (подсказано!)
назвать одной величиной:
,
то есть
.
2). Так мы хотим,
чтобы функция
была решением уравнения (1), необходимо
подставить её в исходное уравнение (по
определению!)!.. Так как
,
после подстановки
и
в (1) получаем:
,
или (так как
)
. (2)
3). Уравнение (2)
есть уравнение с разделяющимися
переменными! Исследуем равенство:
.
Если имеется такое число
,
что
,
то
,
или
есть решение уравнения (1).
4). Теперь примем:
.
Уравнение (2) запишем в виде:
.
Его интегрирование даёт общий интеграл
(решение):
. (3)
5). Будем считать,
что интеграл в выражении (3) удалось
вычислить:
.
Если в последнем заменить
,
получим общий интеграл уравнения (1):
.
Однородные
уравнения 1-порядка вида:
. (4)
1). Если в записи
(4) функции
и
однородные одного порядка, то его легко
преобразовать к виду (1).
2). Как всегда,
сначала попробуем выделить решения
уравнения, используя (4). Если при значении
случится
,
то прямая
есть решение уравнения. Если при значении
случится
,
то прямая
есть решение уравнения.
3). Теперь, принимая
и
,
уравнение (4) запишем в форме (1):
.
Далее по общему алгоритму!..
••• ≡ •••
Пример
1–47:
Решить дифференциальное уравнение:
. (1)
Решение:
1). Прежде всего, отметим, что исходное уравнение (1) имеет очевидное решение .
2).
Так как в заданном уравнении правая
часть зависит только от отношения
неизвестных, то это уравнение –
однородное! Примем
и запишем:
=
=
.
3). Исследуем
равенство:
,
в нашем случае
.
Из тригонометрии известно решение
последнего:
,
или
–
семейство прямых, проходящих через
начало координат
.
При значении
получаем
упомянутое в п. 1) решение
.
4). Теперь примем
и вычислим интеграл
=
=
.
5). Для функции
получено общее решение:
=
,
или
.
Учитывая, что
,
перепишем общее решение использованием
:
.
Ответ:
–
общее решение ДУ, также:
,
.
Пример
2–50:
Решить дифференциальное уравнение:
. (1)
Решение:
1).
Прежде всего, отметим, что исходное
уравнение (1) имеет очевидное решение
.
2). Видим, в записи
(1) функции
и
однородные порядка 1. Учитывая, что
теперь
,
запишем уравнение (1) в виде:
=
. (2)
3). Запишем:
=
.
Вычислим интеграл
=
=
.
4). Для функции
получено общее решение:
=
,
или
.
Учитывая, что
,
перепишем общее решение использованием
:
,
удобнее
.
Ответ: – общее решение ДУ, также x=0 (из общего не выделяется ни при каком ).
Пример
3–55:
Решить дифференциальное уравнение:
. (1)
Решение:
Замечание:
так
как переменная может принимать как
значения
,
так и
,
необходимо рассмотреть оба случая!
0). Прежде всего, отметим, что исходное уравнение (1) не предлагает простейших решений вида: и .
Случай-1, когда x>0:
1).
Разделим равенство (1) на положительное
значение
.
Получим: y′
=
+
.
2).
Так как в заданном уравнении правая
часть зависит только от отношения
неизвестных, то это уравнение –
однородное! Примем
и запишем:
=
=
.
3). Исследуем
равенство:
,
в нашем случае
.
Получаем решение в виде:
,
или
.
4). Теперь примем
и вычислим интеграл
=
=
.
5). Для функции
получено общее решение:
=
,
или
.
Учитывая, что
,
перепишем общее решение использованием
:
.
Ответ: – общее решение ДУ; также .
Случай-2, когда x<0:
1). Разделим равенство (1) на отрицательное значение . Получим: y′ = – .
2).
Так как в заданном уравнении правая
часть зависит только от отношения
неизвестных, то это уравнение –
однородное! Примем
и запишем:
=
=
.
3). Исследуем
равенство:
,
в нашем случае
.
Получаем решение в виде:
,
или
.
4). Теперь примем
и вычислим интеграл
=
=
.
5). Для функции
получено общее решение:
=
,
или
.
Учитывая, что
,
перепишем общее решение использованием
:
.
Ответ: – общее решение ДУ; также .
Замечание: многие Случай-2 не выделяют (в шахматах это называют зевок)!..
Пример
4–56:
Решить дифференциальное уравнение:
. (1)
Решение:
1).
Прежде всего, отметим, что исходное
уравнение (1) имеет очевидное решение
,
в то же время решение
невозможно.
2). Видим, в записи
(1) функции
и
однородные 2-го порядка. Принимая
и
,
запишем уравнение (1) в виде:
=
=
=
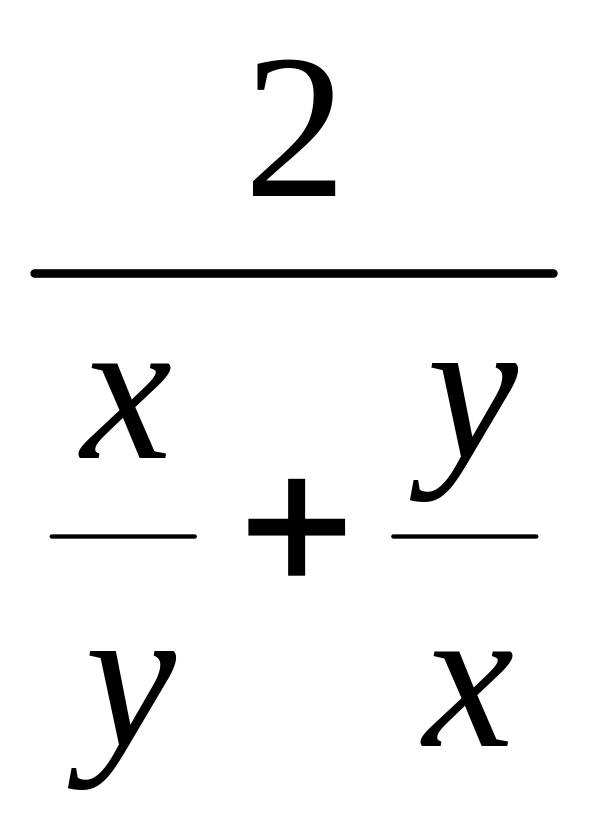. (2)
3). Примем
и запишем выражение:
.
Исследуем равенство:
,
в нашем случае
.
Так как
,
то
.
Остаётся:
,
или в виде
.
4). Теперь примем
и запишем интеграл
=
.
Вычисление записанного интеграла
(интегрирование дробно-рационального
выражения) процесс весьма
трудоёмкий!.. Очень важно студенту
поддаться чувству лени (в
хорошем смысле этого слова – сделать
дело, но с меньшими напряжениями сил!)
и поискать другой способ решения! А
другой способ всего один – считать
решением функцию
.
5). Повторив, с точностью до обозначений, все предыдущие действия получим уравнение:
=
=
. (3)
6). Примем
и запишем выражение:
.
Исследуем равенство:
,
в нашем случае
.
Получаем:
,
или в виде
.
7). Теперь примем
и вычислим интеграл
=
=
.
8). Для функции
получено общее решение:
=
,
или
.
Учитывая, что
,
перепишем общее решение использованием
:
.
Ответ:
– общее решение ДУ; также
.
Решение
может быть получено формально из общего
решения при значении:
.
Пример
5–59:
Решить дифференциальное уравнение:
. (1)
Решение:
1).
Прежде всего, отметим, что исходное
уравнение (1) имеет очевидное решение
.
Равенство нулю множителя при дифференциале
не может дать решения уравнения, так
как при выполнении условия:
имеем
.
2).
Заданное ДУ – специального
вида:
с учётом
его нетрудно преобразовать к виду:
=
.
(2)
3).
Уравнение вида (2) достаточно просто
приводится к однородному уравнению,
которое мы уже умеем решать! Так как
прямые
:
и
:
пересекаются, то для перехода к однородному
уравнению используют преобразование
параллельного переноса начала координат
исходной системы
в точку пересечения этих прямых:
,
.
Для нахождения величин
решим систему уравнений:
Нетрудно получить значения:
.
4).
Применяя преобразование:
,
,
перепишем дифференциальное уравнение
(2): 
–
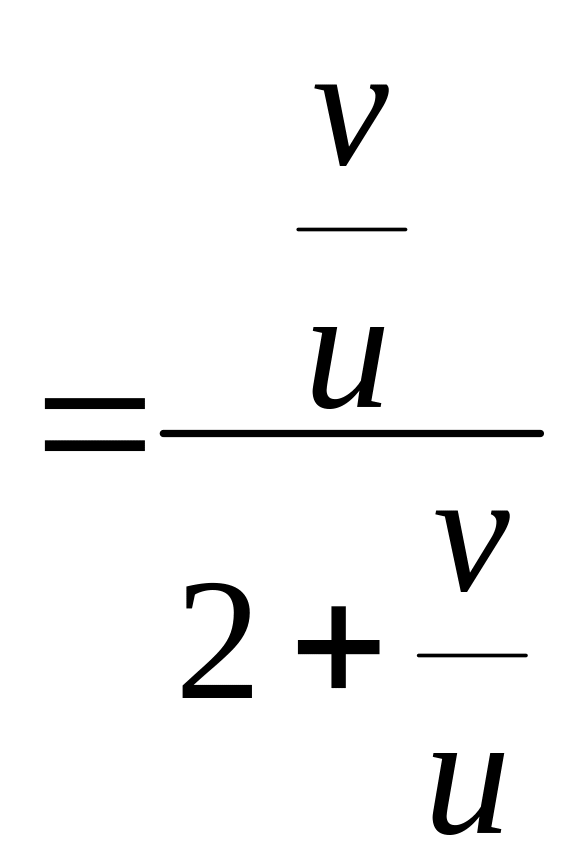однородное
уравнение. (3)
5). Примем
и запишем выражение:
.
Исследуем равенство:
,
в нашем случае
.
Получаем два решения:
и
,
или
и
,
или
и
.
6).
Пусть теперь
.
Вычислим интеграл:
=
=
.
Применяя правила интегрирования
дробно-рациональных выражений, запишем:
=
=
. (5)
8). Для функции
получено общее решение:
=
,
или
.
Учитывая, что
,
а также
,
перепишем общее решение использованием
функции
,
используемой в исходном уравнении:
.
Ответ: – общее решение ДУ, также и (которое выделяется из общего при значении ).
Пример
6–60:
Решить дифференциальное уравнение:
. (1)
Решение:
1). Прежде всего, отметим, что исходное уравнение (1) не имеет очевидных решений.
2).
Заданное ДУ – специального
вида:
с учётом
его нетрудно преобразовать к виду:
=
.
(2)
3).
Нетрудно заметить, что прямые
:
и
:
параллельны.
В этом частном случае задача решается
преобразованием уравнения к виду – с
разделяющимися переменными!
4).
Примем:
.
Учитывая
,
уравнение (2) преобразуем к виду:
. (3)
5).
Из записи (3) легко видеть решение:
,
или
.
Это решение можно было заметить и из
исходной записи, но из записи (3) оно
очевидно!
6).
Интегрирование уравнения (3):
=
,
или
=
.
Учитывая
,
запишем окончательно для общего решения:
Ответ: – общее решение ДУ, также (из общего решения не выделяется ни при каком значении ).
Пример
7–62:
Решить дифференциальное уравнение:
.
(1)
Решение:
1).
Уравнение (1) только слегка похоже на
уравнение специального вида. Преобразуем
дробь, которая является аргументом
тангенса:
=
=
–2.
Теперь видим уравнение вида:
,
то есть специального вида. Нетрудно
заметить, что прямые
:
и
:
перпендикулярны,
то есть пересекаются! Для перехода к
однородному уравнению используют
преобразование параллельного переноса
начала координат исходной системы
в точку пересечения этих прямых (–1,–2).
Эта точка определяет преобразование
переменных:
,
.
2).
Применяя преобразование:
,
,
перепишем дифференциальное уравнение
.
Легко получаем уравнение: 
. (2)
3). Примем
и запишем выражение:
.
Исследуем равенство:
,
у нас:
.
Получаем решения:
,
,
или
,
или
,
или
– семейство прямых линий.
4).
Пусть теперь
.
Вычислим интеграл:
=
=
.
Применяя таблицу интегралов, запишем:
=
.
5). Для функции
получено общее решение:
=
.
Учитывая, что
,
а также
,
перепишем общее решение с использованием
функции
:
.
Ответ: – общее решение ДУ, также , .
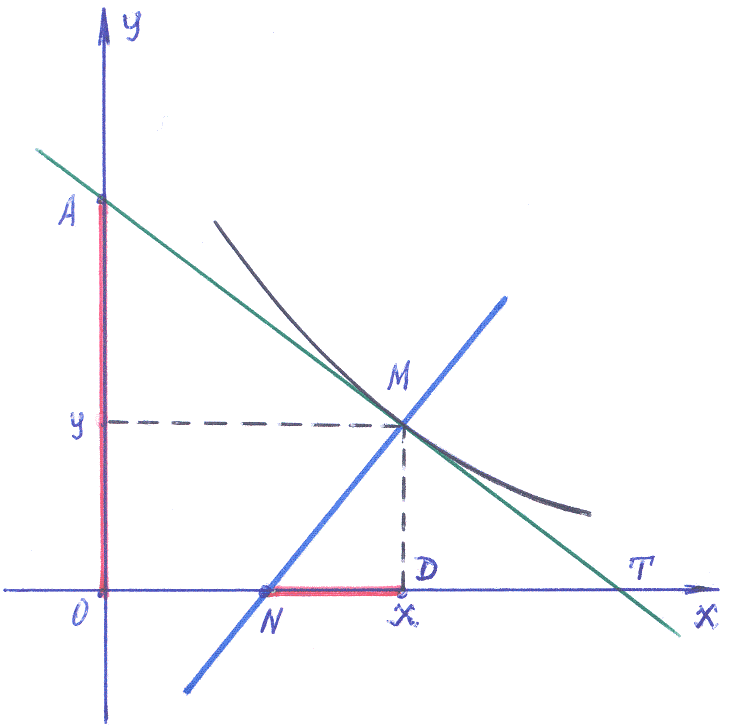
Пример 8–177: Найти уравнение кривой, проходящей через точку (3,1), если длина отрезка, отсекаемого любой её касательной на оси ординат, равна поднормали.
В
Примере
1–19
Главы 1 пособия получены выражения:
для отрезка OA
=
,
отсекаемого касательной на оси ординат,
и ND
=D–N=(x,0)
–
=
–
поднормаль.
Решение:
1).
Учитывая, что точки A
и
M
могут располагаться по одну сторону от
оси ОХ и по разные, запишем два варианта
использования условия задачи
=
:
▪
Случай-1:
=
; (1)
▪ Случай-2:
=
. (2)
Случай-1.
2). Нетрудно заметить из (1) решение , но оно нам не потребуется! Теперь примем и преобразуем уравнение (1) к виду:
. (3)
3). Примем
и, используя (3), запишем выражение:
1.
Это значит, что в этом случае дополнительных
решений нет. Вычислим интеграл
=
=
.
4). Для функции
получено общее решение:
=
,
или, учитывая, что
,
получаем общее решение использованием
:
,
или
. (4)
Случай-2.
5).
На
этот раз уравнение (2)
запишем в виде:
. (5)
6). Примем
и, используя (5), запишем выражение:
.
Это значит, что и в этом случае
дополнительных решений нет. Вычислим
интеграл
=
=
.
7). Для функции
получено общее решение:
=
,
или, учитывая, что
,
получаем общее решение использованием
:
,
или
. (6)
8).
Через точку (3,1)
в Случае-1 проходит интегральная кривая:
,
в Случае-2 кривая
. (5)
Ответ:
–
общее решение ДУ; частное решение:
.
☻
Вопросы для самопроверки:
Какое уравнение называют дифференциальным?
Что такое решение ДУ, частное решение ДУ?
Что такое общее решение ДУ?
Что значит решить Задачу Коши?
Каковы стандартные формы однородных уравнений?
Какова стандартная схема решения однородных уравнений?
Какова стандартная форма уравнений, приводящихся к однородным уравнениям?
Задачи для самоподготовки:
Пример
C3–1:
Решить дифференциальное уравнение:
.
Ответ:
– общее решение ДУ.
Пример
C3–2: Решить
дифференциальное уравнение:
.
Ответ:
– общее решение ДУ, также
и
.
Пример
C3–3: Решить
дифференциальное уравнение:
.
Ответ:
– общее решение ДУ, также
,
.
Пример
C3–4: Решить
дифференциальное уравнение:
.
Ответ:
– общее решение ДУ, также
.
Пример
C3–5: Решить
дифференциальное уравнение:
,
y(1)=1.
Ответ:
Общее решение:
и
;
частное решение:
.
Пример C3–6: Найти уравнение кривой, проходящей через точку (1,0), если длина отрезка оси абсцисс, отсекаемая её нормалью на 2 больше абсциссы точки касания.
Ответ:
– частное решение: парабола;
–
частное решение: эллипс.
< * * * * * >
ЗАНЯТИЕ 4. Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли.
☺ ☻ ☺
Дифференциальное уравнение 1-порядка называют линейным, если входящие в него искомая функция и ее производная входят в уравнение в 1-й степени. Запись линейного уравнения считаем стандартной, если она имеет вид:
, (1)
где
и
–
непрерывные
функции переменной
или постоянные.
Для формы записи (1) используем стандартный алгоритм решения уравнения:
1.
Решение уравнения ищем в виде функции:
,
где
и
.
2.
Вычисляем интеграл:
и записываем выражение:
=
.
3.
Вычисляем:
=
,
где произвольная постоянная величина
,
в зависимости от конкретных выражений
для функций
и
,
может быть записана и в виде выражений
,
и др.
4.
Запишем общее решение уравнения:
=
∙
.
Замечание: Для того, чтобы формально (как предписанную технологию) применять стандартный алгоритм решения линейного уравнения, первым действием при решении линейного уравнения 1-го порядка всегда должно быть приведение конкретного уравнения к форме записи (1)!..
••• ≡ •••
Пример
1–67:
Решить
дифференциальное уравнение:
. (1)
Решение:
1).
Уравнение (1) соответствует стандартной
форме:
и
.
2). Вычисляем
интеграл:
=
=
и записываем выражение:
=
=
.
3). Вычисляем:
=
=
+
=
+
=
+
.
4). Запишем общее
решение уравнения:
=
∙
.
Ответ: = ∙ – общее решение.
Пример
2–68:
Решить
дифференциальное уравнение:
. (1)
Решение:
1).
Приводим уравнение (1) к стандартной
форме:
.
2). Вычисляем
интеграл:
=
=
.
Тогда:
=
=
,
или
=
.
Замечание:
в
последней записи выражения для функции
знак модуля опущен, так как от функции
требуется только обеспечить выполнение
равенства:
(это показано в Пособии при получении
алгоритма решения линейного уравнения).
3). Вычисляем:
=
=
+
=
+
.
4). Запишем общее
решение уравнения:
=
∙
=
.
Ответ: = – общее решение.
Пример
3–74:
Решить
дифференциальное уравнение:
=
. (1)
Решение:
1). Прежде всего, отметим, что исходное уравнение (1) имеет очевидное решение .
2).
Теперь принимаем
и приводим уравнение к стандартной
форме:
.
(2)
Замечание:
Переход
от записи решения в виде функции
к записи
подсказан исходным выражением (1) вполне
выразительно!..
3). Решение уравнения
ищем в виде функции:
,
где
и
.
4). Вычисляем
интеграл:
=
=
.
Тогда:
=
=
,
или
=
.
5). Вычисляем:
=
=
+
=
+
.
6). Запишем общее
решение уравнения:
=
∙
=
.
Ответ: = – общее решение. Из исходного уравнения также: – решение.
Пример
4–78:
Решить
дифференциальное уравнение:
. (1)
Решение:
1).
Приводим уравнение (1) к стандартной
форме:
.
2). Вычисляем
интеграл:
=
=
.
Получаем:
=
=
,
или (удобнее!)
=
.
Замечание: в последней записи выражения для функции знак модуля опущен, так как от функции требуется только обеспечить выполнение равенства: (это показано в Пособии при получении алгоритма решения линейного уравнения).
3). Вычисляем:
=
=
+
=
.
4). Запишем общее
решение уравнения:
=
∙
=
.
Ответ: = – общее решение.
Пример
5–83:
Решить
дифференциальное уравнение:
,
y(0)=0. (1)
Решение:
1).
Уравнение (1) соответствует стандартной
форме:
и
.
2). Вычисляем
интеграл:
=
=
.
Получаем:
=
=
,
или (удобнее!)
=
.
Замечание: в последней записи выражения для функции знак модуля опущен, так как от функции требуется только обеспечить выполнение равенства: (это показано в Пособии при получении алгоритма решения линейного уравнения).
3). Вычисляем:
=
=
+
=
.
4). Запишем общее
решение уравнения:
=
∙
=
.
8). Через точку (0,0) проходит интегральная кривая: , так как =0.
Ответ: = – общее решение; – частное решение.
☺ ☻ ☺
Дифференциальные уравнения 1-порядка Бернулли в стандартной записи:
, (1)
где
и
–
непрерывные
функции переменной
или постоянные,
–
произвольное
число.
Уравнение Бернулли интересно тем, что использованием стандартного приёма приводится к линейному уравнению, которое мы уже умеем решать!.. Вот этот приём:
1.
Применим подстановку:
и перепишем (1):
.
2.
Обозначив:
=
и
=
,
запишем:
– линейное уравнение в стандартной
форме.
Замечание: Для того, чтобы формально (как предписанную технологию) применять стандартный алгоритм решения уравнения Бернулли, первым действием всегда должно быть приведение конкретного уравнения к форме записи (1)!..
••• ≡ •••
Пример
6–86:
Решить
дифференциальное уравнение:
. (1)
Решение:
1).
Уравнение (1) есть уравнение Бернулли в
стандартной форме для значения
,
при этом имеем:
и
.
2). Применим
подстановку:
=
и перепишем (1) как:
,
то есть:
,
или
,
где
=
,
=
.
3). Далее применяем
стандартный алгоритм решения линейного
уравнения:
,
записанного в стандартной форме, приняв
.
4). Вычисляем
интеграл:
=
=
и записываем выражение:
=
=
.
5). Вычисляем:
=
+
=
+
=
=
+
.
6). Запишем общее решение уравнения: = ∙ , или = ∙ .
Ответ:
=
∙
–
общее решение.
Пример
7–92:
Решить
дифференциальное уравнение:
. (1)
Решение:
1).
Уравнение (1) относительно
очевидно не есть линейное, потому искать
в нём признаки уравнения Бернулли нет
смысла! Остаётся поискать линейность
относительно
.
Перепишем уравнение (1): 
. (2)
2).
Уравнение (2) есть уравнение Бернулли в
стандартной форме для значения
,
при этом имеем:
и
.
Далее решаем стандартно!..
3). Применим
подстановку:
=
и перепишем (2) как:
,
то есть:
,
или
,
где
=
,
=
.
4). Далее применяем стандартный алгоритм решения линейного уравнения: , записанного в стандартной форме, приняв .
5). Вычисляем
интеграл:
=
=
и записываем выражение:
=
=
.
Замечание:
в
последней записи выражения для функции
знак модуля опущен, так как в исходном
уравнении
предполагается
.
6). Вычисляем:
=
+
=
+
=
+
.
7). Запишем общее
решение уравнения:
=
∙
,
или
=
∙
.
Ответ:
– общее решение уравнения.
Пример
8–95:
Решить
дифференциальное уравнение:
,
y
=1.
(1)
Решение:
1).
Очевидно: (1) не является уравнением
Бернулли для y,
y′.
Это подсказывает необходимость перехода
к функции
:
x′+
x=
x3. (2)
2).
Уравнение (2) есть уравнение Бернулли в
стандартной форме для значения
,
при этом имеем:
и
.
Далее решаем стандартно!..
3). Применим
подстановку:
=
и перепишем (2) как:
,
то есть:
,
или
,
где
=
,
=
.
4). Далее применяем стандартный алгоритм решения линейного уравнения: , записанного в стандартной форме, приняв .
5). Вычисляем
интеграл:
=
=
и записываем:
=
=
.
6). Вычисляем:
=
+
=
+
=
+
.
7). Запишем общее
решение уравнения:
=
∙
,
или
=
.
8).
Через точку
проходит интегральная кривая:
,
так как
=3.
Ответ:
– общее решение уравнения; частное
решение:
.
Пример
9–179:
Найти
уравнение кривой, проходящей через
точку (1,0), если площадь трапеции,
образованной касательной в этой точке,
осями координат и ординатой точки
касания, постоянна и равна
.
В Примере 1–19 Главы 1 пособия получено выражение: для отрезка OA = , отсекаемого касательной на оси ординат, причём D =(x,0).
Р
ешение:
1).
Так как площадь трапеции вычисляется
по формуле: S=
h,
где a
и b
–
стороны оснований, h
–
высота трапеции, условие задачи запишем
так:
▪ Случай-1:
; (1)
▪ Случай-2:
. (2)
Случай-1.
2). Нетрудно заметить из (1) что и преобразуем уравнение (1) к виду:
. (3)
3). Уравнение (3)
есть линейное уравнение стандартной
формы. Вычисляем интеграл:
=
=
.
Получаем:
=
=
.
4
).
Вычисляем:
=
=
+
=
.
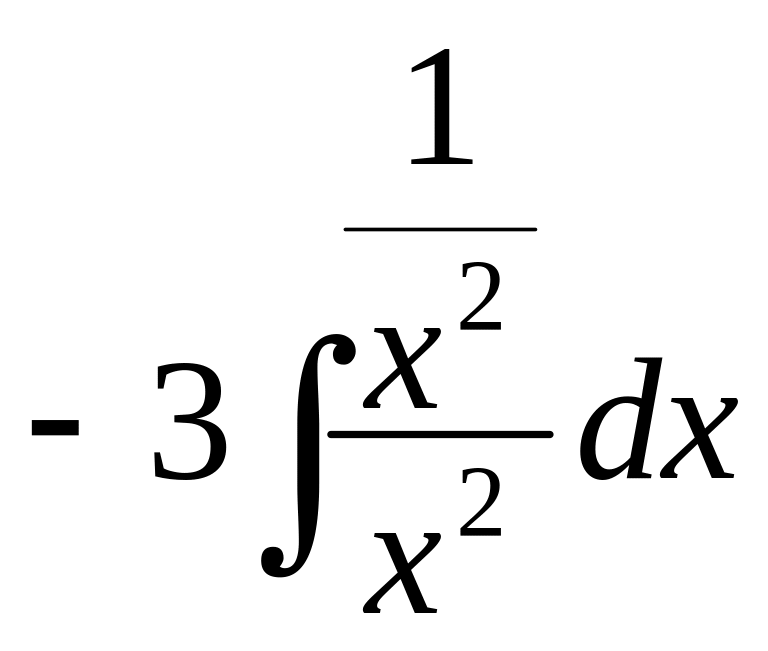5). Запишем общее
решение уравнения:
,
или
=
∙
=
.
Частное решение получается при значении
,
именно:
.
6). Полезно построить эскиз графика интегральной кривой, проходящей через точку (1,0): . На рисунке показано, как получается нужная кривая: это сумма хорошо известных функций гиперболы и параболы. Заметим, что мы должны использовать только график для значений !
Случай-2.
7).
Перепишем уравнение (2): 
.
(4)
8). И в этом случае
получаем:
=
.
Очевидно, и выражение для функции
получаем:
=
.
9). Общее решение
уравнения:
=
∙
=
.
Частное решение получается при значении
,
именно:
,
этот график симметричен относительно
графику, построенному для Случая-1
(выделено красным цветом!).
Ответ:
– общее решение ДУ; частное решение:
,
заметим,
что мы должны использовать только график
для значений
!
Замечание: Если не заметить присутствия двух различных вариантов решения рассмотренной задачи, то зеркальное решение будет потеряно. В задачах физики это дополнительно подсказывает важность понимания начальных условий исследуемого процесса: возможно исследователю потребуются дополнительные эксперименты для уточнения особенностей протекания процесса.
Пример 10–193: Лодка замедляет свое движение под действием сопротивления воды, которое пропорционально скорости лодки. Начальная скорость лодки 1.5 м/с, скорость её через 4 секунды равна 1м/с. Когда скорость уменьшится до 1 см/с? Какой путь пройдет лодка до остановки?
Решение:
Для решения задачи необходимо уточнить: система координат, используемая при решении задачи, связана с берегом реки и считается инерциальной. Это значит, что второй закон Ньютона в этой системе выполняется и можно записать дифференциальное уравнение:
, (1)
г
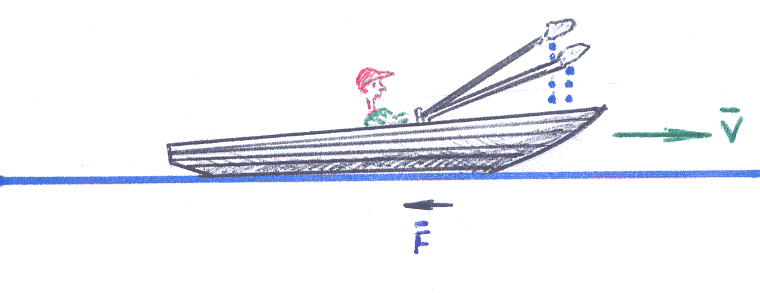де
–
масса лодки с гребцом;
–
коэффициент торможения лодки из-за
сопротивления воды. Движение лодки
происходит по инерции (гребец сушит
весла!).
Для
удобства записи используемых выражений
обозначим:
и запишем уравнение в виде, удобном
для интегрирования: 
=
. (2)
Интегрируя
(2),
получаем общее решение:
,
где
–
начальная скорость движения лодки, у
нас
M/с.
Следует обратить внимание на то, что в
задаче не определены ни движущаяся
масса, ни коэффициент трения лодки о
воду – это дополнительные волнения для
того, кто решает задачу!.. Но, мы имеем
дополнительные сведения (легко
устанавливается экспериментально!),
которые позволят полностью определить
закон движения лодки.
Из
условия: через 4 секунды движения, то
есть
=4c,
наблюдаемая скорость уменьшилась до
величины
=
1 [м/с] → Можем записать равенство:
,
откуда:
≈
0.67. Обозначим
и запишем:
≈
.
Итак,
закон движения лодки в процессе
торможения:
,
у нас
.
После этого можем определить время,
когда скорость лодки уменьшилась до
M/с.
Используя закон движения лодки, запишем
равенство:
,
откуда → t
≈
50 c.
Для
ответа на второй вопрос необходимо
проинтегрировать уравнение:
.
Примем, что начальное положение лодки:
.
Тогда
=
≈
15 м.
Замечание: при вычислении несобственного интеграла учтено, что для верхнего предела значение этого интеграла равно нулю!
Ответ: Время: t ≈ 50 c. До полной остановки лодка переместится на расстояние x ≈ 15 м (это будет проистекать бесконечно долго!).
☻
Вопросы для самопроверки:
Как определяют линейное дифференциальное уравнение 1-го порядка?
Что значит: «стандартная форма» линейного уравнения, зачем её вводят?
Какова основная «идея» способа «подстановки» решения линейного уравнения?
Всегда ли можно «проинтегрировать» линейное ДУ?
Какие уравнения относят к уравнениям Бернулли?
В чем особенность интегрирования уравнения Бернулли?
Бывают ли уравнения Бернулли, которые невозможно «проинтегрировать»?
Задачи для самоподготовки:
Пример
C4–1:
Решить дифференциальное уравнение:
.
Ответ:
=
– общее решение ДУ.
Пример
C4–2: Решить
дифференциальное уравнение:
.
Ответ:
=
– общее решение ДУ.
Пример
C4–3: Решить
дифференциальное уравнение:
.
Ответ:
– общее решение ДУ, также
.
Пример
C4–4: Решить
дифференциальное уравнение:
,
y
=1.
Ответ:
– общее решение ДУ, также
,
частное:
.
Пример C4–5: Найти уравнение кривой, проходящей через точку (0,1), если площадь треугольника, образуемого осью абсцисс, касательной и радиус-вектором точки касания, постоянна и равна 1.
Ответ:
– общее решение ДУ;
частное решение:
,
заметим, что мы должны
использовать только график для значений
!
Пример
C4–6: Сила
тока
в цепи с сопротивлением
,
индуктивностью
и напряжением u удовлетворяет
уравнению:
.
Найти силу тока i в
момент времени t, если
и
при начальном значении
,
(
–
постоянные).
Ответ:
=
– частное решение.
< * * * * * >
ЗАНЯТИЕ 5. Уравнения в полных дифференциалах.
Дифференциальное
уравнение 1-порядка
называют уравнением в
полных дифференциалах, если
входящие в него функции
и
непрерывны и дифференцируемы, а также
выполняется условие:
=
,
причём частные производные
и
– непрерывные функции в некоторой
области
.
Для решения дифференциального уравнения в полных дифференциалах используем стандартный алгоритм:
1.
Проверяем выполнение условия:
=
.
Если условие выполняется, то заданное
уравнение есть уравнение в полных
дифференциалах. Решение ищем в виде
функции
.
2. Имея
функцию
=
,
находим функцию:
=
+
,
где
отражает ту
часть функции
,
которая была потеряна при дифференцировании:
.
Для удобства обозначим:
=
3.
Функцию
находим из условия
=
,
или
+
=
.
Для этого необходимо проинтегрировать:
=
–
,
то есть вычислить интеграл:
=
.
4. Запишем решение: = + = .
••• ≡ •••
Пример
1–96: Решить
дифференциальное уравнение:
,
предварительно убедившись, что оно
является уравнением в полных дифференциалах.
Решение:
1). Проверим выполнение условия: = . У нас: =1 и =1 → заданное уравнение есть уравнение в полных дифференциалах.
2). Вычислим интеграл:
=
=
=
.
3). Вычислим
производную:
=
и запишем условие:
=
–
.
Для заданного уравнения:
=
=
.
4). Вычислим интеграл:
=
=
=
.
5). Запишем решение: = + = . У нас: + = .
Ответ: + = – общее решение.
Пример
2–98: Решить
дифференциальное уравнение:
,
предварительно убедившись, что оно
является уравнением в полных дифференциалах.
Решение:
1).
Проверим выполнение условия:
=
.
У нас:
=
и
=
→ заданное уравнение есть уравнение
в полных дифференциалах.
2). Вычислим интеграл:
=
=
=
.
3). Вычислим
производную:
=
и запишем условие:
=
–
.
Для заданного уравнения:
=
=
.
4). Вычислим интеграл:
=
=
=
.
5). Запишем решение: = + = . У нас: = .
Ответ: = – общее решение.
Замечания:
1).
Пример
интересен тем, что заданное ДУ можно
отнести и к однородным уравнениям:
функции
и
–
однородные порядка 2.
Если попробовать решать его по схеме
однородного уравнения, то трудоёмкость
процесса возрастет в разы: f(u)–u=
–u=
→ J=
.
2).
Ещё
большим будет интерес, если обратить
внимание на ситуацию возможного
равенства: 
=0.
По основной теореме алгебры мы получим
(!) три корня:
,
,
→
получаем дополнительно три решения
ДУ:
,
,
–
прямые, проходящие через начало координат.