
- •Теоретическая механика
- •Содержание
- •Предисловие
- •Задачи по теме: «Плоская система сходящихся сил». Определение опорных реакций, исходя из условия равновесия в аналитической форме.
- •Задачи по теме: «Плоская система произвольно расположенных сил». Определение опорных реакций, исходя из условия равновесия в аналитической форме.
- •Задачи по теме: «Пространственная система произвольно расположенных сил». Определение опорных реакций, исходя из условия равновесия в аналитической форме.
- •Задачи по теме: Определение положения центра тяжести плоских фигур.
- •Задачи по теме: «Кинематика точки». Поступательное движение.
- •Задачи по теме: «Кинематика точки». Вращательное движение.
- •Задачи по теме: «Кинематика точки». Сложное движение.
- •Задачи по теме : «Кинематика твёрдого тела». Плоское движение.
- •Задачи по теме: «Динамика».
- •Список литературы.
Федеральное агентство по образованию Российской Федерации
Филиал “СЕВМАШВТУЗ” государственного учреждения высшего профессионального образования “Санкт-Петербургский государственный морской технический университет”
в г. Северодвинске
Курзанова Е.В.
Теоретическая механика
СБОРНИК ЗАДАЧ
Северодвинск
2012
УДК. 531
Теоретическая механика. Сборник задач. /Сост.
Е.В. Курзанова, Северодвинск: РИО СЕВМАШВТУЗА, 2012 г. – с.
Сборник задач предназначен для студентов всех специальностей, изучающих курс «Теоретическая механика».
В сборнике подробно рассмотрены задачи по следующим разделам: «Статика», «Кинематика», «Динамика».
Рецензенты:
К.т.н., доцент кафедры №3 Д.В. Кузьмин,
Генеральный директор ЗАО НТЦ «БАЗИС» В.А. Базанов.
Содержание
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА 1
Предисловие 4
Задачи по теме: «Плоская система сходящихся сил». Определение опорных реакций, исходя из условия равновесия в аналитической форме. 5
Задачи по теме: «Плоская система произвольно расположенных сил». Определение опорных реакций, исходя из условия равновесия в аналитической форме. 8
Задачи по теме: «Пространственная система произвольно расположенных сил». Определение опорных реакций, исходя из условия равновесия в аналитической форме. 12
Задачи по теме: Определение положения центра тяжести плоских фигур. 15
Задачи по теме: «Кинематика точки». Поступательное движение. 17
Задачи по теме: «Кинематика точки». Вращательное движение. 23
Задачи по теме: «Кинематика точки». Сложное движение. 25
Задачи по теме : «Кинематика твёрдого тела». Плоское движение. 29
Задачи по теме: «Динамика». 35
Список литературы. 45
Предисловие
Целью сборника задач является оказание помощи студентам при изучении предмета, при решении и защите расчетно-графических работ по теоретической механике.
Сборник задач предназначен для студентов всех специальностей, изучающих курс “Теоретическая механика”.
Задачи по теме: «Плоская система сходящихся сил». Определение опорных реакций, исходя из условия равновесия в аналитической форме.
Задача №1. Определить усилия, возникающие в стержнях кронштейна, если к нему подвешен груз весом Q=100 КГс=1000 н.
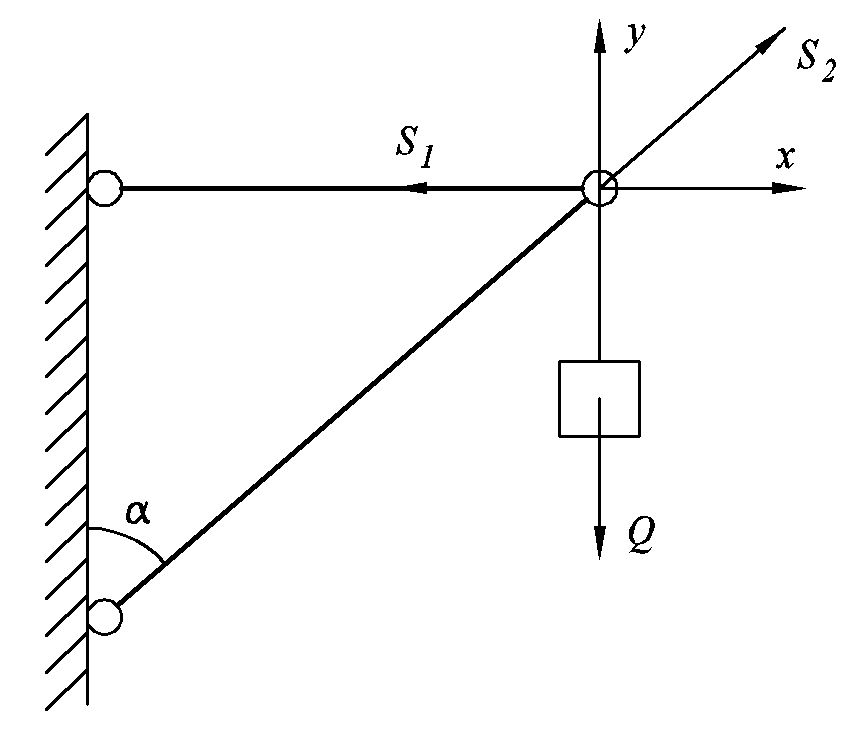
Решение. Изображаем на схеме две реакции связей S1 и S2 . Реакции связей направлены по стержням в стороны, противоположные свободному перемещению груза. Реакция S1 будет направлена к стене и стержень будет растянут. Реакция S2 будет направлена от стены и стержень будет сжат. Получаем плоскую систему сходящихся сил. Выбираем плоскую декартовую систему координат. Точка пересечения всех действующих сил расположена в начале координат. Записываем условие равновесия в аналитической форме, которое состоит из системы двух уравнений.
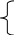 Хi=0
-сумма проекций всех действующих сил
на ось ОХ равна 0.
Хi=0
-сумма проекций всех действующих сил
на ось ОХ равна 0.
Yi=0 -сумма проекций всех действующих сил на ось ОY равна 0.
Проецируем действующие силы на координатные оси:
Хi=
-S1+
S2![]() 0
=
0
0
=
0
Yi=
S2![]() 0
_
Q = 0
0
_
Q = 0
S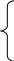 2
2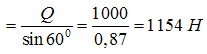
![]()
Ответ: S1=577 Н ; S2=1154 Н.
Задача №2. Шарик весом Р , размерами которого можно пренебречь, подвешен на нерастяжимой нити. Длина нити l .Касается идеально гладкой сферической поверхности радиусом r . Расстояние от точки подвеса нити до сферической поверхности равно d . Найти натяжение нити Т и реакцию сферической поверхности Q.
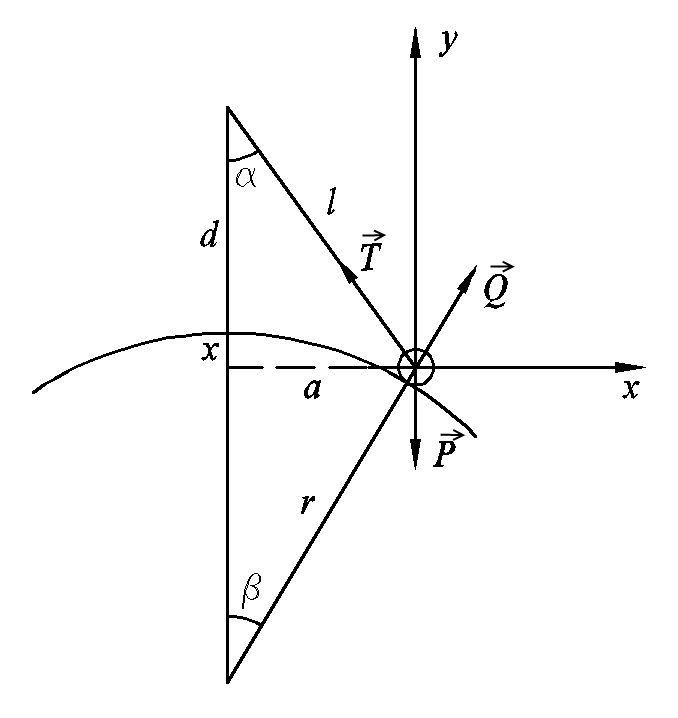
Решение. Изображаем активную силу Р и реакции связей Т и Q. Получаем плоскую систему сходящихся сил. Дополнительно обозначаем углы α и β.
Достраиваем до прямоугольного треугольника и обозначаем полученные расстояния а и х.
Используем тригонометрическую зависимость:
![]()
Получаем:
![]()
Записываем условия равновесия и проецируем действующие силы на координатные оси:
Хi=
-Т![]() +
Q
+
Q![]() = 0
= 0
Yi=
T![]() + Q
+ Q![]() =
0
=
0
T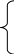 =
=![]() (1)
(1)
![]() (2)
(2)
Если рассматривать прямоугольные треугольники, то из рисунка следует:
![]()
![]()
следовательно:
d
+ r
=![]()
из уравнения (2)
получаем:
![]()
из уравнения (1)
получаем:
![]()
