
Модуль 1.2. Проверка гипотез о равенстве дисперсий, f – критерий Фишера
В некоторых клинических исследованиях о положительном эффекте свидетельствует не столько величина исследуемого параметра, сколько его стабилизация, уменьшение его колебаний. В этом случае возникает вопрос о сравнении двух генеральных дисперсий по результатам выборочного обследования. Эта задача может быть решена с помощью критерия Фишера.
Постановка задачи
Получены две выборки {Х1} и {X2},
извлеченные из генеральных совокупностей
с нормальным законом распределения.
Объемы выборок n1 и
n2, а выборочные
дисперсии равны
![]() соответственно. Требуется сравнить
между собой генеральные дисперсии.
соответственно. Требуется сравнить
между собой генеральные дисперсии.
Проверяемые гипотезы:
Н0 – генеральные дисперсии одинаковы;
Н1 – генеральные дисперсии различны.
Показано, если выборки извлечены из генеральных совокупностей с нормальным законом распределения, то при справедливости гипотезы Н0 отношение выборочных дисперсий подчиняется распределению Фишера. Поэтому в качестве критерия для проверки справедливости Н0 берется величина F, вычисляемая по формуле
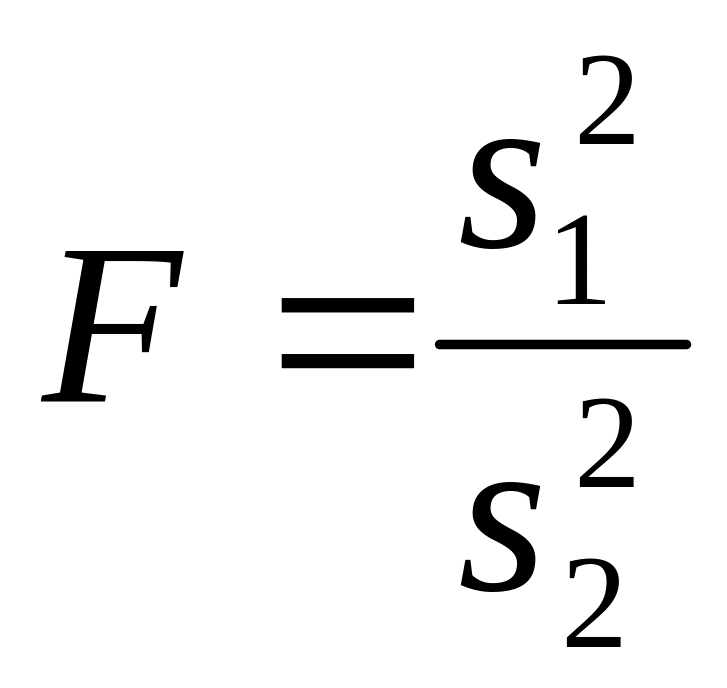 ,
,
где - выборочные дисперсии.
Это отношение подчиняется распределению Фишера с числом степеней свободы числителя 1 = n1 – 1, и числом степеней свободы знаменателя 2 = n2 – 1. Границы критической области находятся по таблицам распределения Фишера или с помощью компьютерной функции FРАСПОБР.
Фрагмент таблицы представлен ниже.
Если значение критерия попадает в критическую область, то принимается гипотеза Н0. В противном случае принимается гипотеза Н1.
Применение критерия Фишера
Способность критерия Фишера обнаруживать различия между генеральными дисперсиями тем выше, чем больше объемы выборок и чем больше величина отношения генеральных СКО больш/меньш. Для демонстрации этого обстоятельства сформированы нарастающие по объему выборки.
а) Сначала сформированы выборки n = 30, мень = 1, боль = 1,25 больш/меньш = 1,25.
Для проверки гипотезы о равенстве генеральных дисперсий из этих выборок последовательно брались группы нарастающего объема: n = 10; n = 20; n = 25; n = 30.
Для облегчения работы студентов подсчитаны выборочные дисперсии (s2) и СКО (s), приведенные ниже. Студентам предлагается вычислить значение критерия F, найти границы критической области по таблицам Фишера (фрагмент таблицы помещен ниже) и сформулировать результат проверки.
Pбольш/меньш = 1,25 |
|
Границы критической области для выборок одинакового объема = 0.05 (P = 0.95) |
|||||||
|
|||||||||
выборки |
B1 |
B2 |
|
B1 |
B2 |
|
|||
|
1 |
1,25 |
|
1 |
1,25 |
|
|||
n |
10 |
10 |
|
20 |
20 |
|
|||
|
|
|
|
|
|
|
|
Fлев |
Fправ |
|
20,833 |
19,411 |
|
20,833 |
19,411 |
|
5 |
0,140 |
7,146 |
|
20,044 |
21,685 |
|
20,044 |
21,685 |
|
6 |
0,172 |
5,820 |
|
19,290 |
20,129 |
|
19,290 |
20,129 |
|
7 |
0,200 |
4,995 |
|
18,929 |
18,464 |
|
18,929 |
18,464 |
|
8 |
0,226 |
4,433 |
|
20,237 |
19,468 |
|
20,237 |
19,468 |
|
9 |
0,248 |
4,026 |
|
19,032 |
19,616 |
|
19,032 |
19,616 |
|
10 |
0,269 |
3,717 |
|
21,479 |
18,980 |
|
21,479 |
18,980 |
|
11 |
0,288 |
3,474 |
|
21,267 |
19,603 |
|
21,267 |
19,603 |
|
12 |
0,305 |
3,277 |
|
20,271 |
22,365 |
|
20,271 |
22,365 |
|
13 |
0,321 |
3,115 |
|
22,306 |
20,743 |
|
22,306 |
20,743 |
|
14 |
0,336 |
2,979 |
|
|
|
|
20,787 |
17,199 |
|
15 |
0,349 |
2,862 |
|
|
|
|
20,365 |
20,546 |
|
16 |
0,362 |
2,761 |
s2 |
1,240 |
1,479 |
|
19,169 |
19,549 |
|
17 |
0,374 |
2,673 |
s |
1,114 |
1,216 |
|
20,737 |
21,659 |
|
18 |
0,385 |
2,596 |
|
|
|
|
21,338 |
19,829 |
|
19 |
0,396 |
2,526 |
границы |
Fлев |
Fправ |
|
19,643 |
20,936 |
|
20 |
0,406 |
2,464 |
0,248 |
4,026 |
|
20,609 |
23,518 |
|
21 |
0,415 |
2,409 |
|
F |
0,84 |
|
21,697 |
19,731 |
|
22 |
0,424 |
2,358 |
|
Принята |
Но |
|
19,480 |
21,851 |
|
23 |
0,433 |
2,312 |
|
|
|
|
|
20,323 |
18,664 |
|
24 |
0,441 |
2,269 |
|
|
|
|
|
|
|
25 |
0,448 |
2,230 |
|
|
|
|
|
|
|
26 |
0,456 |
2,194 |
|
|
|
s2 |
0,894 |
2,222 |
|
27 |
0,463 |
2,161 |
|
|
|
s |
0,945 |
1,491 |
|
28 |
0,470 |
2,130 |
|
|
|
|
|
|
|
29 |
0,476 |
2,101 |
|
|
|
границы |
Fлев |
Fправ |
|
30 |
0,482 |
2,074 |
|
|
|
0,396 |
2,526 |
|
31 |
0,488 |
2,049 |
|
|
|
|
F |
0,402 |
|
32 |
0,494 |
2,025 |
|
|
|
|
Принята |
Но |
|
33 |
0,499 |
2,002 |
|
|
|
|
|
|
|
|
34 |
0,505 |
1,981 |
Pбольш/меньш = 1,25 |
|||||
выборки |
B1 |
B2 |
|
B1 |
B2 |
|
1 |
1,25 |
|
1 |
1,25 |
n |
25 |
25 |
|
30 |
30 |
|
|
|
|
|
|
|
20,833 |
19,411 |
|
20,833 |
19,411 |
|
20,044 |
21,685 |
|
20,044 |
21,685 |
|
19,290 |
20,129 |
|
19,290 |
20,129 |
|
18,929 |
18,464 |
|
18,929 |
18,464 |
|
20,237 |
19,468 |
|
20,237 |
19,468 |
|
19,032 |
19,616 |
|
19,032 |
19,616 |
|
21,479 |
18,980 |
|
21,479 |
18,980 |
|
21,267 |
19,603 |
|
21,267 |
19,603 |
|
20,271 |
22,365 |
|
20,271 |
22,365 |
|
22,306 |
20,743 |
|
22,306 |
20,743 |
|
20,787 |
17,199 |
|
20,787 |
17,199 |
|
20,365 |
20,546 |
|
20,365 |
20,546 |
|
19,169 |
19,549 |
|
19,169 |
19,549 |
|
20,737 |
21,659 |
|
20,737 |
21,659 |
|
21,338 |
19,829 |
|
21,338 |
19,829 |
|
19,643 |
20,936 |
|
19,643 |
20,936 |
|
20,609 |
23,518 |
|
20,609 |
23,518 |
|
21,697 |
19,731 |
|
21,697 |
19,731 |
|
19,480 |
21,851 |
|
19,480 |
21,851 |
|
20,323 |
18,664 |
|
20,323 |
18,664 |
|
20,610 |
20,559 |
|
20,610 |
20,559 |
|
19,066 |
20,257 |
|
19,066 |
20,257 |
|
18,821 |
21,130 |
|
18,821 |
21,130 |
|
19,514 |
21,043 |
|
19,514 |
21,043 |
|
20,082 |
20,035 |
|
20,082 |
20,035 |
|
|
|
|
19,534 |
17,990 |
|
|
|
|
20,154 |
19,968 |
s2 |
0,897 |
1,825 |
|
20,533 |
19,498 |
s |
0,947 |
1,351 |
|
18,992 |
18,731 |
|
|
|
|
19,339 |
19,586 |
границы |
Fлев |
Fправ |
|
|
|
0,441 |
2,269 |
|
|
|
|
F |
0,491 |
s2 |
0,836 |
1,778 |
|
Принята |
Но |
s |
0,914 |
1,334 |
|
|
|
|
|
|
|
|
|
|
границы |
Fлев |
Fправ |
|
|
|
0,476 |
2,101 |
|
|
|
|
F |
0,47 |
|
|
|
|
Принята |
Н1 |
|
В данном случае различие в генеральных дисперсиях обнаружено только при n = 30.
б) Затем генеральное СКО второй выборки увеличено до 1,5 что соответствует больш/меньш = 1,5. При таком отношении различия в дисперсиях обнаруживаются при n = 20.
Pбольш/меньш = 1,5 |
|||||
выборки |
B1 |
B2 |
|
B1 |
B2 |
|
1 |
1,5 |
|
1 |
1,5 |
n |
10 |
10 |
|
20 |
20 |
|
|
|
|
|
|
|
20,833 |
19,293 |
|
20,833 |
19,293 |
|
20,044 |
22,022 |
|
20,044 |
22,022 |
|
19,290 |
20,154 |
|
19,290 |
20,154 |
|
18,929 |
18,156 |
|
18,929 |
18,156 |
|
20,237 |
19,362 |
|
20,237 |
19,362 |
|
19,032 |
19,540 |
|
19,032 |
19,540 |
|
21,479 |
18,776 |
|
21,479 |
18,776 |
|
21,267 |
19,524 |
|
21,267 |
19,524 |
|
20,271 |
22,838 |
|
20,271 |
22,838 |
|
22,306 |
20,892 |
|
22,306 |
20,892 |
|
|
|
|
20,787 |
16,638 |
|
|
|
|
20,365 |
20,655 |
s2 |
1,240 |
2,130 |
|
19,169 |
19,458 |
s |
1,114 |
1,459 |
|
20,737 |
21,991 |
|
|
|
|
21,338 |
19,794 |
границы |
Fлев |
Fправ |
|
19,643 |
21,123 |
0,248 |
4,026 |
|
20,609 |
24,222 |
|
F |
0,582 |
|
21,697 |
19,677 |
|
Принята |
Но |
|
19,480 |
22,222 |
|
|
|
|
|
20,323 |
18,397 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 |
0,894 |
3,200 |
|
|
|
s |
0,945 |
1,789 |
|
|
|
|
|
|
|
|
|
границы |
Fлев |
Fправ |
|
|
|
0,396 |
2,526 |
|
|
|
|
F |
0,279 |
|
|
|
|
Принята |
Н1 |
|
В данном случае различие генеральных дисперсий обнаруживается на выборках меньшего размера
