Решение
1. Реакции опор
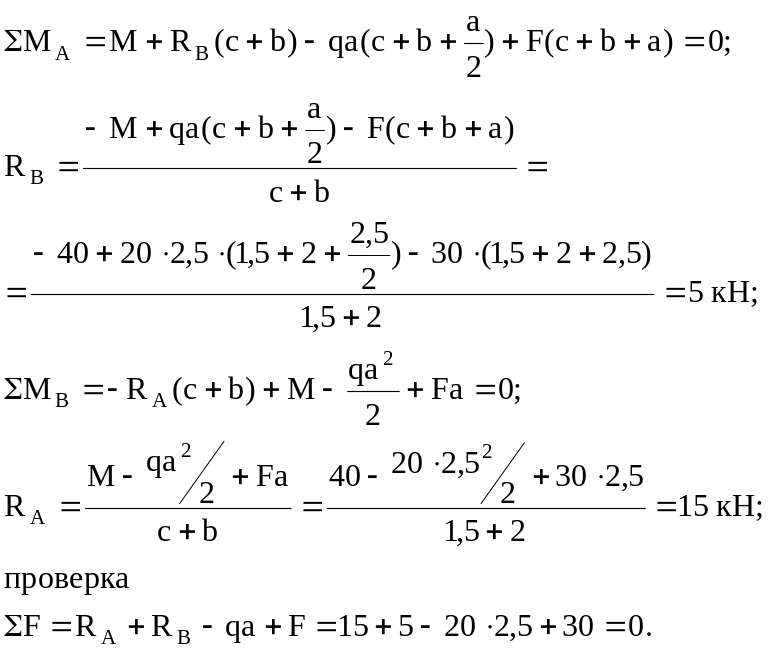
2. Эпюра поперечных сил:
на участке c суммируем силы слева от сечения: Q1=RA=15 кН;
на участке b суммируем силы слева от сечения: Q2=RA=15 кН;
на
участке a
суммируем
силы справа от сечения:
3. Эпюра изгибающих моментов:
на участке c суммируем моменты сил слева от сечения
на участке b суммируем моменты сил слева от сечения
на
участке a
суммируем
моменты сил справа от сечения
и результаты расчетов сводим в таблицу,
z3 |
0 |
0,25 a |
0,5 a |
0,75 a |
a |
l |
M3 |
0 |
14,84 |
21,87 |
21,1 |
12,5 |
22,5 |
где
l – координата z3
сечения, в котором Q=0 и, следовательно,
производная от изгибающего момента
равная нулю
4.
Момент сопротивления при изгибе
максимальным моментом М = 22,5 кН·м.
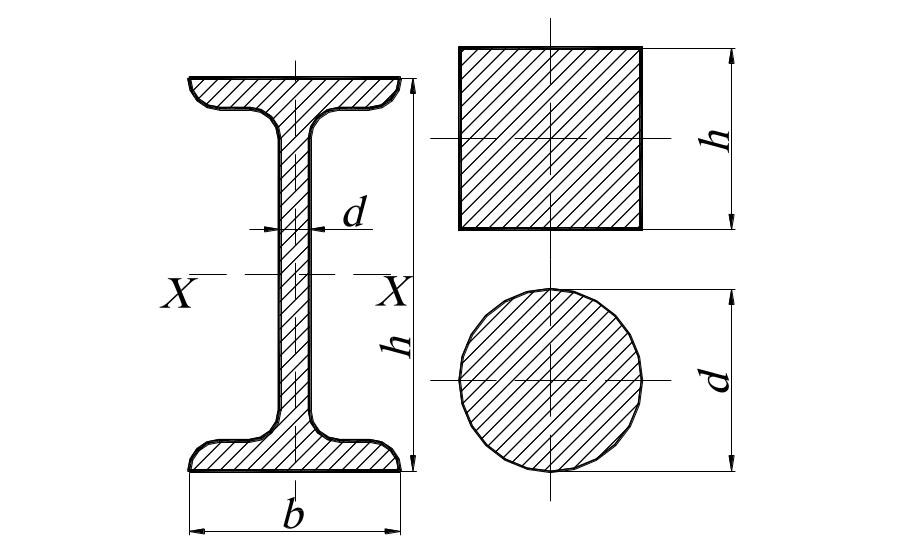
По таблице сортамента выбираем двутаровое сечение №18а, у которого Wx = 159 см3, Jx = 1430 см4, Sx*=89,8 см3, А = 6,4 см2, h = 180 мм, b = 100 мм,
d = 5,1 мм, t = 8,3 мм.
Сторона квадратного сечения
Диаметр круглого сечения
5. Сечение балки в масштабе 1:2
6. Площади сечений:
двутаврового
(из таблицы сортамента) Адв
= 2540 мм2;
квадратного Акв=h2=9409
мм2;
круглого
наименьшая площадь у балки двутаврового
сечения.
Отношение площадей поперечных сечений
7. Максимальные касательные напряжения от наибольшей поперечной силы Q=30 кН в сечениях:
двутавровом
квадратном
круглом
Задача 5
Реакции опор определяем, приравнивая нулю сумму моментов всех сил в данной плоскости относительно каждой опоры. При правильном решении сумма проекций на плоскость сечения всех сил в каждой плоскости равна нулю. Изгибающие и крутящие моменты находим по методу сечений, учитывая правила знаков.
Пример 5
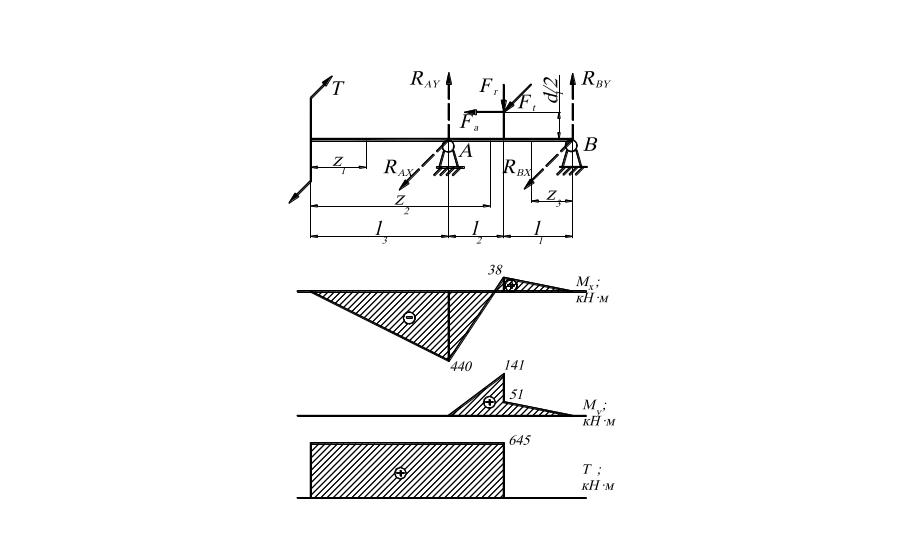
Вал нагружен в горизонтальной плоскости силами Ft=6450 Н, FM=2750 Н, в вертикальной плоскости силами Fr=2400 Н, Fa=900 Н. Размеры l1=80 мм, l2=80 мм, l2=160 мм, d1=200 мм. Требуется:
1) определить реакции опор и построить эпюры изгибающих моментов М в горизонтальной и вертикальной плоскостях;
2) построить эпюру крутящих моментов Т.
РЕШЕНИЕ
1. Реакции опор в горизонтальной плоскости
2. Реакции опор в вертикальной плоскости
3. Эпюра изгибающих моментов в горизонтальной плоскости:
на участке l3 в пределах изменения z1 от 0 до l3
на участке l2 в пределах изменения z2 от l3 до (l3+l2)
на
участке l1
в пределах
изменения z3
от 0 до l1
4. Эпюра изгибающих моментов в вертикальной плоскости:
на
участке l3
на
участке l2
на
участке l1
на границе участков l1 и l2 эпюра MY имеет скачок, равный сосредоточенному моменту Fd·d1/2.
5.
Крутящий момент на участках l2
и
l3
определяем из условия равновесия вала
Задача 6
Расчетную схему балки располагаем в прямоугольной системе координат XYZ. Начало координат помещаем в заделке, ось Z направляем по оси балки, а ось Y – в плоскости изгиба балки. Составляем дифференциальное уравнение оси изогнутой балки, после двукратного интегрирования, которого получаем уравнения для вычисления углов поворота θ = Y' и прогибов Y. Постоянные интегрирования определяем из условий закрепления (граничных условий) балки.
Пример 6
Определить прогиб Y и угол поворота θ сечения конца консольной балки длиной l = 1 м круглого сечения диаметра d = 40 мм, нагруженной распределенной нагрузкой q = 200 Н/м, сосредоточенной силой F = 110 Н и изгибающим моментом М = 40 Н·м. Материал балки – сталь с модулем продольной упругости Е = 2·105 МПа.
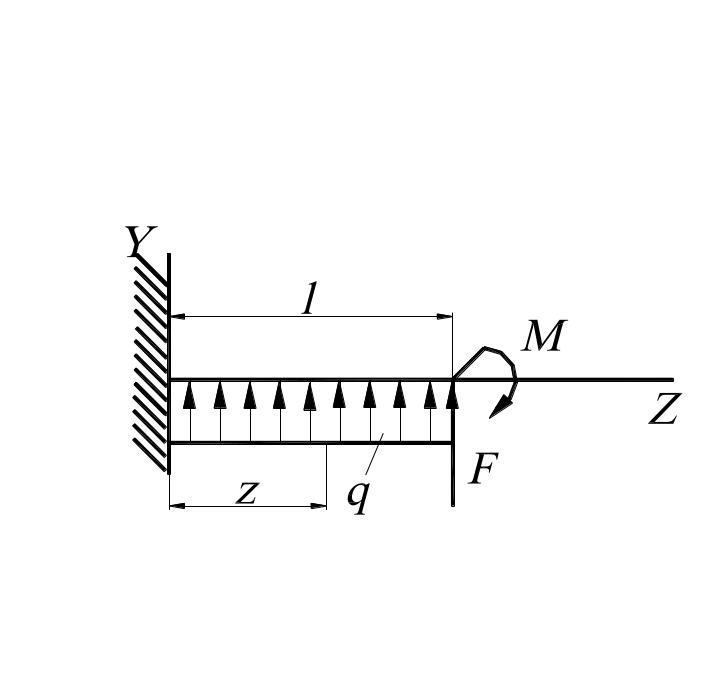
РЕШЕНИЕ
1. Дифференциальное уравнение оси изогнутой балки большой жест кости имеет вид
где Y'' – кривизна оси балки в плоскости изгиба на расстоянии z от заделки;
MZ – изгибающий, момент на расстоянии Z от заделки;
Е – модуль продольной упругости материала балки;
JX – момент инерции сечения балки относительно оси перпендикулярной к плоскости изгиба.
2. Изгибающий момент в сечении z равен
следовательно, дифференциальное уравнение оси изогнутой балки принимает вид
(1)
3. Интегрируя уравнение (1), получаем
(2)
При z = 0 по условиям закрепления балки (жесткая заделка) угол поворота сечения Y´ = 0, тогда С1 = 0.
4. Момент инерции круглого сечения балки
5. Угол поворота сечения на конце балки находим из уравнения (2) при z = l
6. Интегрируем уравнение (2)
(3)
При z=0 имеем Y=0, тогда С2=0.
7. Прогиб конца балки находим из уравнения (3) при z = l
