3. Булева алгебра

Пусть A, B и D - произвольные подмножества множества . Тогда непосредственно из определений объединения, пересечения и дополнения вытекают следующие предложения:

1) (замкнутость операций объединения и пересечения);

2) (коммутативность операций объединения и пересечения);

3) (ассоциативность операций объединения и пересечения);

4) (дистрибутивность операции объединения относительно операции пересечения);

(дистрибутивность операции пересечения относительно операции объединения);

5) ;

6) ;

7) ;

8) .

Если для элементов множества определены объединение и пересечение , для которых выполняются отношения 1) ÷ 8), то тройка называется булевой алгеброй. Таким образом, если σ – семейство всех частей множества , то – булева алгебра.

Общие указания.

Изучить выше представленные теоретические положения и выполнить практическую часть работы.

Приведенные ниже примеры являются общими для всех вариантов.

Примеры

• Доказать справедливость отношений 1) ÷ 8)

• Доказать принцип двойственности: C(A U B) = CA ∩ CB, C(A ∩ B) = CA U CB.

• Доказать равенства A U (A ∩ B) = A ∩ (A U B) = A.

• Доказать равенства:

CCА = А,

СJ = Ø,

CØ =J.

• Доказать справедливость включения .

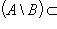
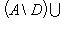
• Определить множества A U B, A ∩ B, A\B, B\A, A Δ B, если:               а) A = {x: 0 < x < 2}, B = {x: 1 ≤ x ≤ 3};               б) A = {x: x² - 3x < 0}, B = {x: x² - 4x + 3 ≥ 0};               в) A = {x: |x - 1| < 2}, B = {x: |x - 1| + |x - 2| < 3}.

• Имеем

= . Показать, что .

• Пусть A = {x: 2 ≤ x ≤ 4}, B = {y: 1 ≤ y ≤ 3}. Изобразить на плоскости ХOУ множество точек A × B.

В случае невыполнения отдельных зданий необходимо представить реальный процесс (попытку) получения результата и сформулировать вопрос (вопросы), непонимание которых привело к отрицательному результату.

Таблица вариантов

Следующее задание носит индивидуальный характер, и номер варианта

задания совпадает с порядковым номером студента в журнале группы. ??????????????????????????????????????????????????

Для заданных дискретных множеств {X} и {Y} (таблица 2) представить все указанные в таблице 1 множества. Множество {J} является областью определения множеств {X} и {Y}.

Таблица 1

J={1÷30}

X×Y

CXY

CYX

X/Y

Y/X

X Y

X Y

Таблица 2

№ Вар.	Множество Х по вариантам
1	13	20	10	10	23	28	1	20	16	21	11	28	7	16	10	21	9	2	16	11
2	26	1	9	19	14	4	2	22	3	12	16	14	23	9	28	9	25	14	26	26
3	5	15	25	15	28	8	20	21	26	16	25	21	23	27	10	24	1	5	19	24
4	16	25	10	2	6	7	30	11	28	22	25	22	2	2	1	27	15	28	0	25
5	1	7	12	9	27	7	10	11	24	18	14	25	22	24	26	6	1	28	27	19
6	2	14	27	15	13	21	22	26	16	17	21	12	18	22	22	29	28	23	11	20
7	27	30	28	16	5	8	21	21	8	3	1	1	12	17	30	29	2	13	3	1
8	14	15	21	1	8	15	28	7	26	24	2	5	14	14	4	9	16	1	14	4
9	24	29	21	18	22	18	5	28	6	9	14	14	15	19	12	13	24	21	10	2
10	12	25	7	25	7	26	6	22	22	13	28	10	5	28	10	11	21	11	18	16
11	10	8	24	29	19	14	1	12	15	21	8	3	26	7	25	29	4	24	8	7
12	8	1	9	9	1	26	17	17	12	29	29	28	5	24	20	2	7	27	24	3
13	7	16	25	5	4	22	5	15	24	11	5	7	2	10	6	27	20	29	6	24
14	24	27	13	18	20	9	15	8	6	22	4	23	19	1	27	28	9	26	27	13
15	13	29	11	7	1	7	18	15	17	20	3	17	1	21	14	1	27	12	7	11
16	4	20	30	11	10	14	24	8	3	15	15	7	14	30	18	23	4	10	20	12
17	2	14	2	6	25	29	14	26	23	4	4	14	20	6	4	13	1	27	25	26
18	4	17	11	29	25	28	2	1	19	28	19	18	6	4	16	12	2	27	3	11
19	18	17	16	25	25	9	24	7	15	17	4	9	3	20	23	1	13	26	11	28
20	20	14	14	12	11	23	29	24	17	28	14	9	13	8	3	22	24	22	15	26

Таблица 3

№ Вар.	Множество У по вариантам
1	8	6	6	22	29	21	27	1	30	7	30	22	17	25	1	2	24	30	19	16
2	29	8	26	27	22	24	11	6	3	23	7	2	29	3	1	9	8	9	20	6
3	17	6	7	4	5	10	17	26	9	7	13	2	19	10	26	5	27	1	18	5
4	5	11	9	21	1	24	5	28	27	28	4	10	1	22	17	16	26	13	21	27
5	17	2	19	9	24	1	25	11	17	4	3	10	17	17	6	2	27	30	17	10
6	9	19	21	29	17	26	18	10	26	21	14	26	8	8	5	6	11	7	16	13
7	17	28	27	16	12	28	21	26	23	20	21	1	16	28	6	11	12	15	2	3
8	4	12	18	8	14	9	26	8	18	10	22	23	0	16	2	22	29	30	20	10
9	4	14	25	28	5	19	11	4	3	1	14	13	0	6	6	26	7	8	27	24
10	27	6	13	26	1	14	13	9	8	4	5	26	10	12	30	15	12	15	7	17
11	17	22	8	17	1	24	2	11	5	7	26	7	1	19	16	9	9	1	12	12
12	14	15	16	17	3	15	19	2	7	10	14	6	24	3	21	9	14	6	11	3
13	13	16	10	12	17	26	15	12	19	27	6	4	15	21	21	26	1	29	23	22
14	11	24	4	25	4	9	19	25	20	1	2	8	14	15	27	6	21	24	19	4
15	14	21	14	23	3	11	19	17	17	4	19	18	28	20	3	4	0	28	20	25
16	21	28	6	15	28	8	1	20	26	18	10	14	21	11	11	3	2	17	10	14
17	17	2	2	30	22	17	27	3	27	13	13	6	3	14	26	17	1	18	13	24
18	11	23	15	14	25	22	25	25	8	10	27	28	2	11	22	20	21	17	11	24
19	8	24	12	8	4	18	25	29	22	11	26	19	3	21	14	27	20	12	19	1
20	25	15	20	3	26	22	23	14	11	1	21	3	27	20	25	6	28	4	8	13

Результаты выполнения данного раздела оформить в наглядном, удобном для проверки виде, например в форме таблицы.

Работа 3. Вероятность события. Основные формулы и теоремы теории вероятностей.

Цель работы:

Изучение базовых основ теории вероятности и приобретение навыков решения практических задач с использованием теоретических положений теории вероятности.

Общие указания.

Изучить базовые понятия теории вероятности по материалу, предлагаемому ниже.

Различные определения вероятности случайного события

Теория вероятностей – математическая наука, которая по вероятностям одних событий позволяет оценивать вероятности других событий, связанных с первыми.

Подтверждением того, что понятие «вероятность события» не имеет определения, является тот факт, что в теории вероятностей существует несколько подходов к объяснению этого понятия:

Классическое определение вероятности случайного события.

Вероятность события равна отношению числа благоприятных событию исходов опыта к общему числу исходов опыта.

,

где

– число благоприятных исходов опыта;

– общее число исходов опыта.

Исход опыта называется благоприятным для события , если при этом исходе опыта появилось событие . Например, если событие – появление карты красной масти, то появление туза бубен – исход, благоприятный событию .

Примеры.

1) Вероятность выпадения 5 очков на грани кубика равна , поскольку кубик может упасть любой из 6 граней кверху, а 5 очков находятся только на одной грани.

2) Вероятность выпадения герба при однократном бросании монеты - , поскольку монета может упасть гербом или решкой – два исхода опыта, а герб изображен лишь на одной стороне монеты.

3) Если в урне 12 шаров, из которых 5 – черные, то вероятность вынуть черный шар – , поскольку всего исходов опыта – 12, а благоприятных из них – 5.

Замечание. Классическое определение вероятности применимо при двух условиях:

• все исходы опыта должны быть равновероятными;

• опыт должен иметь конечное число исходов.

На практике бывает сложно доказать, что события равновероятные: например, при произведении опыта с подбрасыванием монеты на результат опыта могут влиять такие факторы как несимметричность монеты, влияние ее формы на аэродинамические характеристики полета, атмосферные условия и т.д., кроме того, существуют опыты с бесконечным числом исходов.

Пример. Ребенок бросает мяч, и максимальное расстояние, на которое он может забросить мяч – 15 метров. Найти вероятность того, что мяч улетит за отметку 3 м.

Решение. Искомую вероятность предлагается считать, как отношение длины отрезка, находящегося за отметкой 3 м (благоприятная область) к длине всего отрезка (всевозможные исходы):

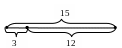
Пример. Точку случайным образом бросают в круг радиуса 1. Какова вероятность того, что точка попадет во вписанный в круг квадрат?

Решение. Под вероятностью того, что точка попадет в квадрат, понимают в данном случае отношение площади квадрата (благоприятной площади) к площади круга (общая площадь фигуры, куда бросают точку):

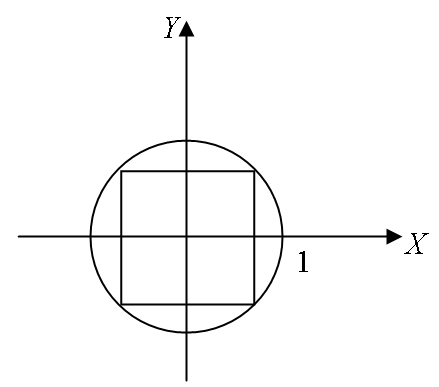
Диагональ квадрата равна 2 и выражается через его сторону по теореме Пифагора:

Аналогичные рассуждения проводят и в пространстве: если в теле объема случайным образом выбирается точка, то вероятность того, что точка окажется в части тела объема , вычисляется как отношение объема благоприятной части к общему объему тела:

.

Объединяя все случаи, можно сформулировать правило вычисления геометрической вероятности:

Если в некоторой области случайным образом выбирается точка, то вероятность того, что точка окажется в части этой области равна:

,

где – обозначает меру области: в случае отрезка – это длина, в случае плоской области – это площадь, в случае пространственного тела – это объем, на поверхности – площадь поверхности, на кривой – длина кривой.

Интересным приложением понятия геометрической вероятности является задача о встрече.

Задача. (О встрече)

Два студента договорились о встрече, например, в 10 часов утра на следующих условиях: каждый приходит в любое время в течение часа с 10 до 11 и ждет 10 минут, после чего уходит. Какова вероятность встречи?

Решение. Проиллюстрируем условия задачи следующим образом: на оси отложим время, идущее для первого из встречающихся, а на оси - время, идущее для второго. Поскольку эксперимент длится один час, то по обеим осям отложим отрезки длины 1. Моменты времени, когда встречающиеся пришли одновременно, интерпретируется диагональю квадрата.

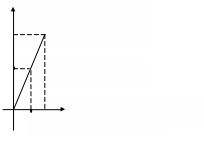
Пусть первый пришел в некоторый момент времени . Студенты встретятся, если время прибытия второго на место встречи заключается в промежутке

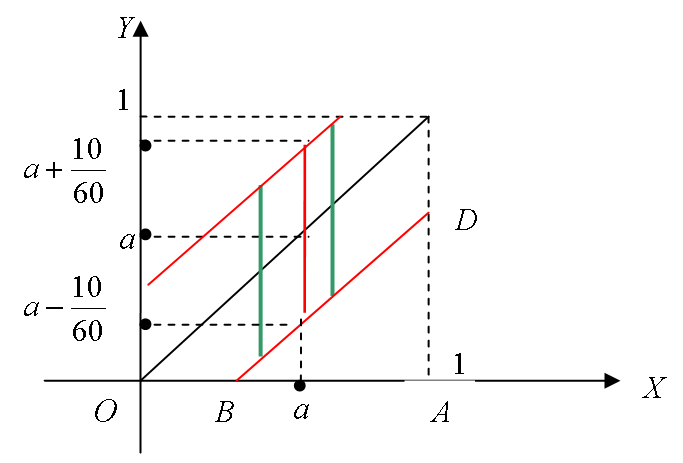
Рассуждая так для любого момента времени , получим, что область времени, интерпретирующая возможность встречи («пересечение времён» нахождения на нужном месте первого и второго студентов) находится между двумя прямыми: и . Вероятность встречи определяется по формуле геометрической вероятности:

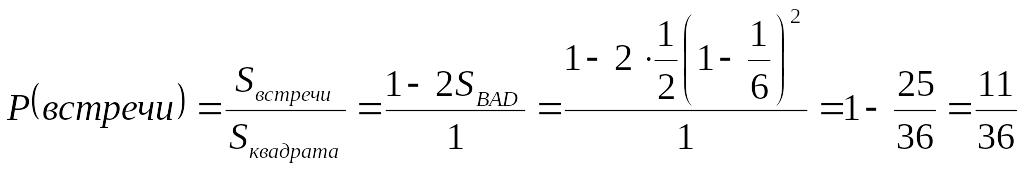
В 1933 г. Колмогоров А.М. (1903 - 1987) предложил аксиоматический подход к построению и изложению теории вероятности, который стал общепринятым в настоящее время. При построении теории вероятности как формальной аксиоматической теории требуется не только ввести базовое понятие – вероятность случайного события, но и описать его свойства с помощью аксиом (утверждений интуитивно верных, принимаемых без доказательства).

Такими утверждениями являются утверждения, аналогичные свойствам относительной частоты появления события.

Относительной частотой появления случайного события называется отношение числа появлений события в испытаниях к общему числу проведенных испытаний:

.

Очевидно, , для достоверного события , для невозможного события , для несовместных событий и верно следующее:

.

Пример. Проиллюстрируем последнее утверждение. Пусть из колоды в 36 карт вынимают карты. Пусть событие означает появление бубей, событие означает появление червей, а событие - появление карты красной масти. Очевидно, события и несовместны. При появлении красной масти ставим метку возле события , при появлении бубей – возле события , а при появлении червей – возле события . Очевидно, что метка возле события будет поставлена тогда и только тогда, когда будет поставлена метка возле события или возле события , т.е. .

Назовем вероятностью случайного события число, сопоставленное событию по следующему правилу:

Для несовместных событий и

Итак,

Относительная частота	Вероятность
,	,

При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это свойство называется свойством устойчивости относительной частоты. Число, около которого группируются относительные частоты появления события при проведении большой сери опытов, может быть принято за вероятность события. Такой способ определения вероятности события называется статистическим определением вероятности.

Например, Дж. Керрих, находясь в лагере во время второй мировой войны, провел 10 серий по 1000 опытов в каждой по бросанию монетки. Относительная частота выпадений герба была следующей:

,

что еще раз подтверждает, что вероятность выпадения герба при одном бросании монетки – 1/2 .

Кроме того, известно, что .

Таким образом, статистическое определение вероятности лучше всех других отражает сущность понятия вероятности случайного события, однако, отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.

Теорема сложения вероятностей и ее следствия

Теорема (сложения вероятностей). Вероятность суммы двух случайных событий равна сумме вероятностей этих событий минус вероятность их пересечения:

.

Доказательство. Очевидно:

;

Тогда

.

Поскольку события и несовместны, то по аксиоме :

.

События и несовместны, и по аксиоме :

.

События и несовместны, по аксиоме :

.

Итак,

Следствие 1: Верно следующее обобщение формулы для трех слагаемых:

Следствие 2: Верно следующее обобщение формулы для слагаемых:

- формула включений и исключений.

Определение. Событие А называется независимым от события В, вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Условная вероятность.

Наступление события может повлиять на вероятность появления события . Для учета таких случаев вводится понятие условной вероятности события .

Определение. Вероятность события , вычисленная при условии, что имело место событие , называется условной вероятностью события и обозначается

.

Пример. Пусть событие – означает, что при бросании двух кубиков на первом выпала 1, а событие – означает, что сумма очков, выпавших на двух костях больше 5. Найти вероятность .

Решение. Если на первом кубике выпала 1, то возможными исходами опыта являются исходы . Событию при этом благоприятствуют исходы , т.е. два из 6, значит,

Теорема умножения вероятностей.

Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило:

Доказательство. Докажем теорему для случая, когда опыт имеет конечное число несовместных равновероятных исходов.

Пусть:

• событие появилось в исходах опыта;

• событие появилось в 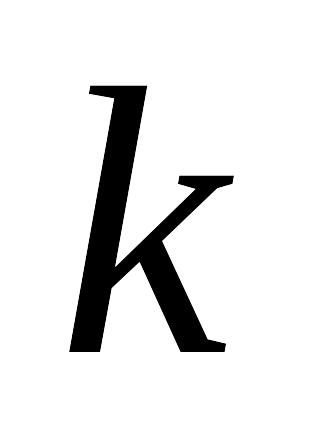исходах опыта;

• событие появилось в 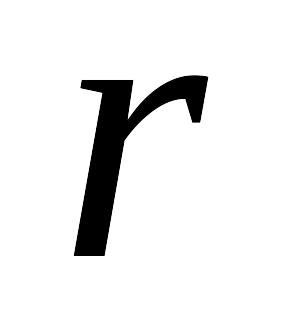исходах опыта.

Вероятность события вычислим по классическому определению. Поскольку событие произошло, то всего возможных в этом случае исходов - ; при этом из этих возможных исходов благоприятны событию те исходы, которые составляют событие , т.е. исходов:

,

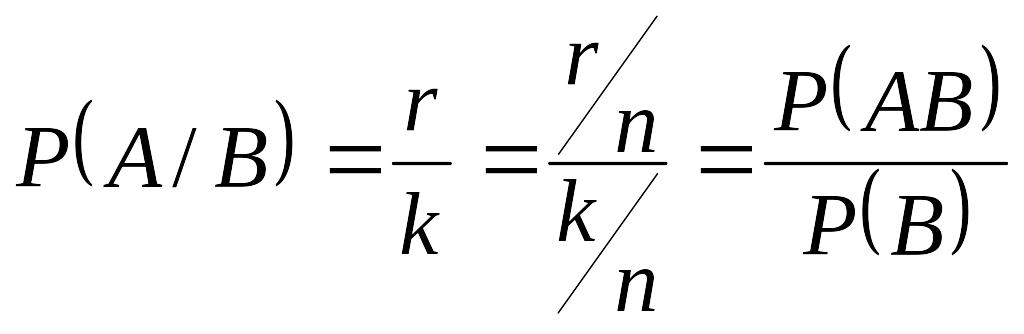или

.

Следствие 1. Обобщим теорему на случай трех событий:

Следствие 2. Обобщим теорему на случай событий: в случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились:

.

Пример. В группе 20 студентов. Из них двое курят, 12 – в очках, 6 – курят и носят очки. Найти вероятность того, что студент курит, если он носит очки.

Решение. Пусть событие - студент курит; - студент носит очки.

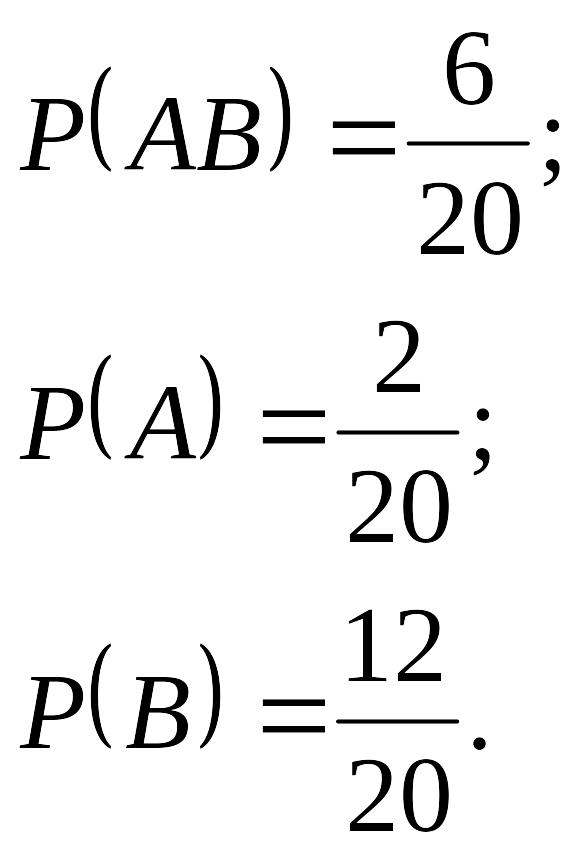
Тогда

.

Заметим, что условная и безусловная вероятности события в данной задаче различны: .

События называются независимыми, если появление одного из них не влияет на вероятность появления другого: .

Если события независимые, то теорема умножения вероятностей принимает вид:

– критерий независимости событий.

В рассмотренном примере события и – зависимы, поскольку

.

Пример. Бросают три монетки и игральную кость. Событие – выпал герб, событие – выпало число очков, равное 6. Пространством элементарных исходов опыта является множество . Тогда , , . Таким образом, , т.е. события и – независимы.

Свойства независимых событий.

Теорема

Если события и независимы, то:

1. события и независимы;

2. события и независимы;

3. события и независимы.

Доказательство.

1)

Поскольку события и независимы, то:

.

Итак,

.

Поскольку , то , что свидетельствует о независимости событий и .

2)

Поскольку события и независимы, то:

.

Итак,

.

Поскольку , то , что свидетельствует о независимости событий и .

3) Если события и независимы, то по 2) события и независимы; и по 1) и независимы.

Определение. События независимы в совокупности, если

.

Определение. События попарно независимы, если в любой паре события и независимы.

Независимость в совокупности и попарная независимость событий – понятия разные.

Пример. Три грани треугольной пирамиды окрашены соответственно в белый, зеленый, желтый цвета. На последней грани присутствуют все три цвета. Случайным образом выбирают грань. Найти вероятности событий:

= «на грани есть желтый цвет»;

= «на грани есть белый цвет»;

= «на грани есть зеленый цвет».

Решение. Желтый цвет имеется на двух гранях из четырех, т.о. ; аналогично: . Вероятность того, что на выпавшей грани есть два цвета - , т.е. . Таким образом,

,

Т.е. все события попарно независимы. Однако события не являются независимыми в совокупности:

Теорема. (О появлении хотя бы одного из независимых событий)

Пусть вероятность появления каждого из п событий , независимых в совокупности, равна . Вероятность появления хотя бы одного события, равна

,

Доказательство. Поскольку по закону Де Моргана

,

то

.

Пример. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая карта.

Решение. Пусть событие означает «среди четырех вынутых карт есть хотя бы одна бубновая карта». Тогда . Событие означает, что все четыре карты не бубновой масти. Вероятность того, что случайно взятая из колоды карта не бубновая - и , тогда ,

Пример. Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах равна 0,875. Найти вероятность попадания в мишень при одном выстреле.

Если обозначить р – вероятность попадания стрелком в мишень при одном выстреле, то вероятность промаха при одном выстреле, очевидно, равна (1 – р).

Вероятность трех промахов из трех выстрелов равна (1 – р)3. Эта вероятность равна 1 – 0,875 = 0,125, т.е. в цель не попадают ни одного раза.

Получаем:

Пример. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей?

Решение.

Вероятность выпадения 6 очков при одном броске кости (событие ) равна . Вероятность того, что не выпадет 6 очков (событие ) - . Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна .

Тогда вероятность того, что хотя бы один раз выпадет 6 очков, равна .

Пример. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза.

Вероятность того, что выстрелы производит первый, второй или третий стрелок равна .

Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:

- для первого стрелка:

- для второго стрелка:

- для третьего стрелка:

Искомая вероятность равна:

Пример. В барабане револьвера находятся 4 патрона из шести в произвольном порядке. Барабан раскручивают, после чего нажимают на спусковой крючок два раза. Найти вероятности следующих событий: первый выстрел, вторая осечка; первая осечка, второй выстрел, хотя бы одного выстрела, двух выстрелов, двух осечек.

Решение. Вероятность выстрела при первом нажатии на курок в условиях задачи - . Вероятность того, что при втором нажатии на курок будет выстрел, если первым был выстрел, - , поскольку неизрасходованных патронов осталось 3, и гнезд, которые могут оказаться напротив бойка 5. Таким образом, вероятность двух последовательных выстрелов

Вероятность осечки при первом нажатии на курок в условиях задачи равна . Вероятность того, что при втором нажатии на курок будет осечка, если первой была осечка, - , поскольку пустых гнезд осталось одно, и гнезд, которые могут оказаться напротив бойка 5. Таким образом, вероятность двух последовательных осечек .

Найдем вероятность события «осечка, выстрел». Вероятность осечки при первом нажатии на курок , неиспользованных патронов остается - 4 , а всего возможных гнезд – 5, т.о. вероятность выстрела при втором нажатии на курок, если при первом нажатии на курок была осечка, - . Тогда вероятность события «осечка, выстрел» - .

Найдем вероятность события «выстрел, осечка». Вероятность выстрела при первом нажатии на курок , пустых гнезд остается - 2 , а всего гнезд – 5, т.о. вероятность осечки при втором нажатии на курок, если при первом нажатии на курок был выстрел, - . Тогда вероятность события «выстрел, осечка» - .

Найдем вероятность хотя бы одного выстрела при двух нажатиях на курок (событие ) . Противоположным событием является событие «ни одного выстрела при двух нажатиях на курок», т.е. две осечки. Тогда равна

.

Найдем вероятность события «осечка, выстрел». Вероятность осечки при первом нажатии на курок , неиспользованных патронов остается - 4 , а всего возможных гнезд – 5, т.о. вероятность выстрела при втором нажатии на курок, если при первом нажатии на курок была осечка, – . Тогда вероятность события «осечка, выстрел» – .

Найдем вероятность события «выстрел, осечка». Вероятность выстрела при первом нажатии на курок , пустых гнезд остается – 2 , а всего гнезд – 5, т.о. вероятность осечки при втором нажатии на курок, если при первом нажатии на курок был выстрел, – . Тогда вероятность события «выстрел, осечка» – .

– два выстрела подряд

– первая осечка, второй выстрел

– первый выстрел, вторая осечка

– две осечки подряд

Эти четыре случая образуют полную группу событий (сумма их вероятностей равна единице)

Анализируя полученные результаты, видим, что вероятность хотя бы одного выстрела равна сумме или

Теперь рассмотрим другой случай. Предположим, что после первого нажатия на курок барабан раскрутили и опять нажали на курок. Условные вероятности второго выстрела и осечки вычисляются из условия, что напротив бойка может оказаться то же гнездо, что и в первый раз.

Вероятности первого выстрела и первой осечки не изменились – ,

Условная вероятность выстрела при второй попытке – если в первый раз был выстрел, – если в первый раз произошла осечка.

Условная вероятность осечки во второй раз – , если в первый раз произошел выстрел, – если была осечка.

Тогда:

– два выстрела подряд

– первая осечка, второй выстрел

– первый выстрел, вторая осечка

– две осечки подряд

В этом случае вероятность того, что произойдет хотя бы один выстрел, равна

Или

	после первого выстрела барабан не раскручивают	после первого выстрела барабан раскручивают

Ниже показаны диаграммы вероятностей для первого и второго рассмотренных случаев.

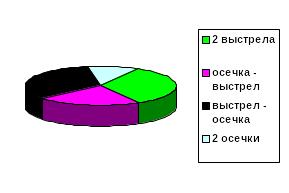
Пример. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

Решение. Обозначим попадание в цель первым стрелком – событие А, вторым – событие В, промах первого стрелка – событие , промах второго – событие .

Вероятность того, что первый стрелок попадет в мишень, а второй – нет равна

Вероятность того, что второй стрелок попадет в цель, а первый – нет равна

Тогда вероятность попадания в цель только одним стрелком равна

Тот же результат можно получить другим способом – находим вероятности того, что оба стрелка попали в цель и оба промахнулись. Эти вероятности соответственно равны:

Тогда вероятность того, что в цель попадет только один стрелок равна:

Пример. Вероятности того, что нужная деталь находится в первом, втором, третьем или четвертом ящике, соответственно равны 0,6, 0,7, 0,8, 0,9. Найти вероятности того, что эта деталь находится: а) не более, чем в трех ящиках; б) не менее, чем в двух ящиках.

Решение.

а) Вероятность того, что данная деталь находится во всех четырех ящиках, равна

Вероятность того, что нужная деталь находиться не более, чем в трех ящиках равна вероятности того, что она не находится во всех четырех ящиках.

.

б) Вероятность того, что нужная деталь находится не менее, чем в двух ящиках, складывается из вероятностей того, что деталь находиться только в двух ящиках, только в трех ящиках, только в четырех ящиках. Конечно, эти вероятности можно посчитать, а потом сложить, однако, проще поступить иначе. Та же вероятность равна вероятности того, что деталь не находится только в одном ящике и имеется вообще.

Вероятность того, что деталь находится только в одном ящике, равна

Вероятность того, что нужной деталь нет ни в одном ящике, равна:

Искомая вероятность равна

Пример. Последовательно послано четыре радиосигнала. Вероятности приема каждого из них не зависят от того, приняты ли остальные сигналы, или нет. Вероятности приема сигналов равны соответственно 0,2, 0,3, 0,4, 0,5. Определить вероятность приема трех радиосигналов.

Событие приема трех сигналов из четырех возможно в четырех случаях:

Для приема трех сигналов необходимо совершение одного из событий А, В, С или D. Таким образом, находим искомую вероятность:

Изучив приведенные теоретические положения по теории вероятности и рассмотрев представленные примеры необходимо перейти к практической части работы.

Задачи на классическое определение вероятности.

0. Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 3 места.

1. Абонент забыл последние 2 цифры телефонного номера, но помнит, что они различны и образуют двузначное число, меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры.

2. Шесть шаров случайным образом раскладывают в три ящика. Найти вероятность того, что во всех ящиках окажется разное число шаров, при условии, что все ящики не пустые.

3. На шахматную доску случайным образом поставлены две ладьи. Какова вероятность, что они не будут бить одна другую?

4. Шесть рукописей случайно раскладывают по пяти папкам. Какова вероятность того, что ровно одна папка останется пустой?

5. Цифры 1, 2, 3, …, 9, выписанные на отдельные карточки складывают в ящик и тщательно перемешивают. Наугад вынимают одну карточку. Найти вероятность того, что число, написанное на этой карточке: а) четное; б) двузначное.

6. На полке в случайном порядке расставлено 40 книг, среди которых находится трехтомник Пушкина. Найти вероятность того, что эти тома стоят в порядке возрастания номера слева направо, но не обязательно рядом.

7. На каждой из пяти одинаковых карточек напечатана одна из следующих букв: "а", "м", "р", "т", "ю". Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной карточке можно прочесть слово "юрта".

8. Ребенок имеет на руках 5 кубиков с буквами: А, К, К, Л, У. Какова вероятность того, что ребенок соберет из кубиков слово "кукла"?

9. В урне находится 12 белых и 8 черных шаров. Найти вероятность того, что два одновременно изъятых наудачу шара будут черными.

0. В мешке лежат 7 синих, 8 красных и 6 зеленых одинаковых по форме шаров. Не глядя, вынимают один шар. Какова вероятность того, что шар окажется зеленым?

1. В коробке «Ассорти» лежат 30 одинаковых по виду шоколадных конфет, из которых 18 штук со сливочной начинкой и 12 штук — с ореховой. Выбираются наугад две конфеты. Какова вероятность того, что обе конфеты окажутся с ореховой начинкой?

2. Выпускники девятого класса выбрали для продолжения образования следующие профили обучения: 7 человек — юридический, 12 человек — экономический, 6 человек — математический и 10 человек — гуманитарный. Какова вероятность того, что случайно встреченный выпускник этого класса выбрал математический профиль обучения?

3. Ученику надо выучить к зачету 32 вопроса. Он выучил 24 вопроса. На зачете он вытягивает два билета из 32, по одному вопросу в каждом. Какова вероятность того, что ответ хотя бы на один вопрос он знает?

4. Случайным образом выбирают одно из решений неравенства

–1 ≤ 2x + 3 ≤ 9.

Какова вероятность того, что оно удовлетворяет неравенству x ≥ 0?

0. Середины сторон прямоугольника являются вершинами ромба. Какова вероятность того, что наугад выбранная точка прямоугольника окажется внутри ромба, если стороны прямоугольника равны 6 см и 8 см?

1. Случайным образом выбирают одно из решений неравенства

x ² – 5x ≤ 24.

Какова вероятность того, что оно удовлетворяет неравенству | x | ≤ 4?

0. Вероятность того, что семена огурцов взойдут, равна 0,84. Сколько семян приблизительно было взято для проращивания, если взошло 140 семян?

1. Вероятность брака при использовании современных высокоточных технологий равна 0,0015. Сколько качественных изделий выпускает предприятие, если число бракованных изделий за исследуемый период было равно 2?

2. Случайным образом выбрали трехзначное число. Какова вероятность того, что сумма его цифр равна 21?

Примечание: номер задачи совпадает с последней цифрой номера зачетной книжки.

Работа 4. Геометрический метод решения задач линейного

программирования.

Цель работы:

Изучение методов решения задач экономического характера на примерах задач линейного программирования.

Общие указания.

Внимательно изучить представленный материал, связанный с методикой применения геометрического метода решения задач линейного программирования.

Основная задача линейного программирования

Основная задача линейного программирования (ОЗЛП) ставится следующим образом: Имеется ряд переменных . Требуется найти такие их неотрицательные значения, которые удовлетворяли бы системе линейных уравнений:

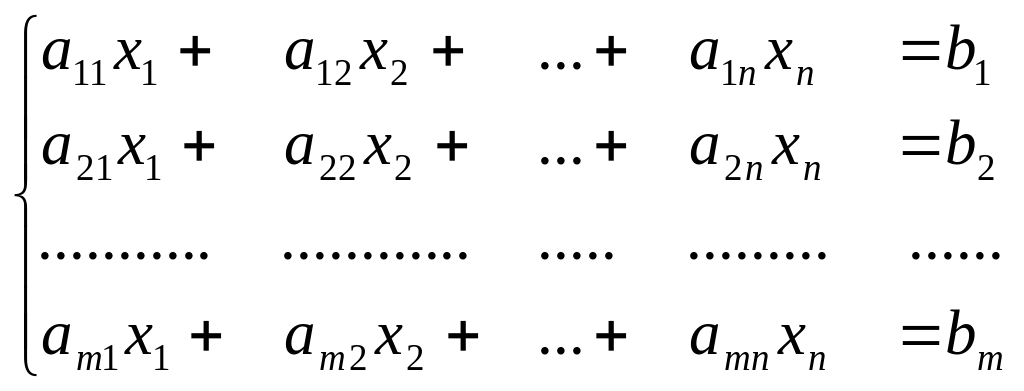{1.1}

и, кроме того, обращали бы в минимум линейную целевую функцию (ЦФ)

Очевидно, случай, когда ЦФ нужно обратить не в минимум, а в максимум, легко сводится к предыдущему, если изменить знак функции и рассмотреть вместо нее функцию

Допустимым решением ОЗЛП называют любую совокупность переменных , удовлетворяющую уравнениям (1.1).

Оптимальным решением называют то из допустимых решений, при котором ЦФ обращается в минимум.

На практике ограничения в задаче линейного программирования часто заданы не уравнениями, а неравенствами. В этом случае можно перейти к основной задаче линейного программирования.

Рассмотрим задачу линейного программирования с ограничениями-неравенствами, которые имеют вид

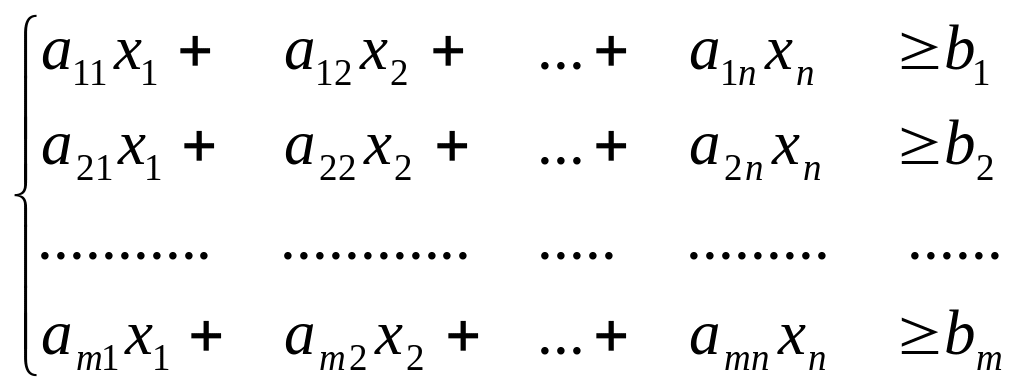{1.2}

и являются линейно-независимыми. Последнее означает, никакое из них нельзя представить в виде линейной комбинации других. Требуется найти , которые удовлетворяют неравенствам и обращают в минимум

Введём уравнения:

{1.3} где – добавочные переменные, которые также как и являются неотрицательными.

Таким образом, имеем общую задачу линейного программирования – найти неотрицательные , чтобы они удовлетворяли системе уравнений (1.3) и обращали в минимум .

Коэффициенты в формуле (1.3) перед равны нулю.

ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Теоретическое введение

Графический метод довольно прост и нагляден для решения задач линейного программирования с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи.

Каждое из неравенств задачи линейного программирования (1.2) определяет на координатной плоскости некоторую полуплоскость (рис.2.1), а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучом, одной точкой. В случае несовместности системы ограничений задачи (1.2) ОДР является пустым множеством.

Все вышесказанное относится и к случаю, когда система ограничений (1.2) включает равенства, поскольку любое равенство

можно представить в виде системы двух неравенств (см. рис.2.1)

ЦФ при фиксированном значении определяет на плоскости прямую линию . Изменяя значения L, мы получим семейство параллельных прямых, называемых линиями уровня.

Это связано с тем, что изменение значения L повлечет изменение лишь длины отрезка, отсекаемого линией уровня на оси (начальная ордината), а угловой коэффициент прямой останется постоянным (см.рис.2.1). Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение L.

Вектор с координатами из коэффициентов ЦФ при и перпендикулярен к каждой из линий уровня (см. рис.2.1). Направление вектора совпадает с направлением возрастания ЦФ, что является важным моментом для решения задач. Направление убывания ЦФ противоположно направлению вектора .

Суть графического метода заключается в следующем. По направлению (против направления) вектора в ОДР производится поиск оптимальной точки . Оптимальной считается точка, через которую проходит линия уровня , соответствующая наибольшему (наименьшему) значению функции . Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.

При поиске оптимального решения задач линейного программирования возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений – единственная точка; задача не имеет решений.

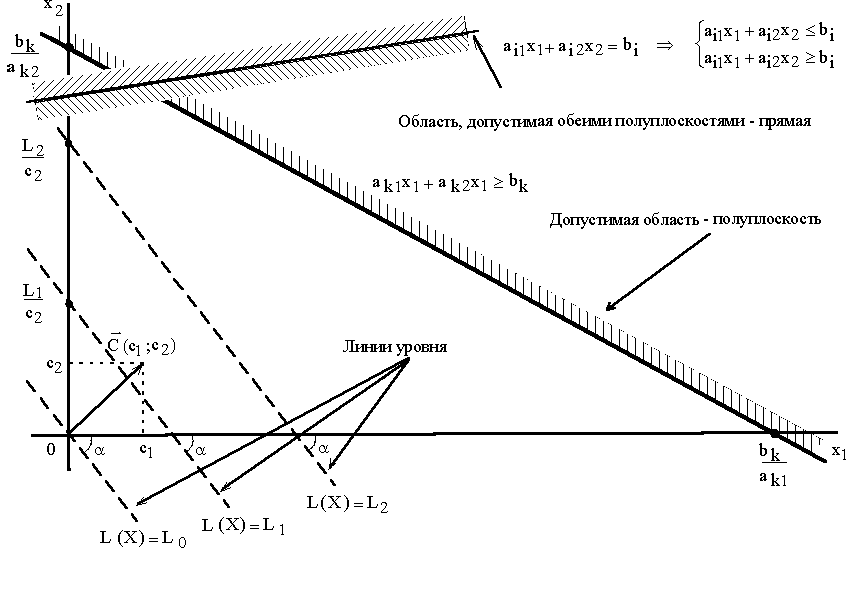
Рисунок 13 Геометрическая интерпретация ограничений и ЦФ задачи.