1.2. Переменная – ее матричный характер

Как и в других языках программирования, в MATLAB’e можно использовать переменные. Имя для переменной, как обычно, должно начинаться с буквы. В имени не должно быть пробелов и специальных символов. Присвоить переменной значение можно с помощью оператора присваивания:

>> var=2

var =

2

После этого вы можете использовать переменную в выражениях наравне с числами:

>> c = 2*var

c =

4

Однако есть в переменных MATLAB’а особенность, отличающая их от переменных других языков программирования. Напомню, что само название MATLAB является сокращением слов MATrix LABoratory – матричная лаборатория. Изначально комплекс был предназначен для матричных вычислений. По этой причине любая переменная считается матрицей. Даже, если в этой матрице только одна строка и один столбец, как в предыдущих примерах. Чтобы присвоить переменной матрицу также можно использовать оператор присваивания:

>> A = [1 2 3; 3 1 -1; 1 0 1]

A =

1 2 3

3 1 -1

1 0 1

Здесь следует обратить внимание на то, что для задания матрицы, во-первых, используются квадратные скобки, во-вторых, строки матрицы разделяются точкой с запятой (;).

Вы можете также присвоить переменной вектор-строку или вектор-столбец:

>> x = [1 1 1]

x =

1 1 1

>> y = [1;1;1]

y =

1

1

1

Векторы рассматриваются как частные случаи матрицы.

Если теперь записать произведение матрицы A на вектор-столбец y, то MATLAB, соответствуя своему названию, вычислит это произведение в строгом соответствии с правилами линейной алгебры:

>> A*y

ans =

6

3

2

Вы можете легко проверить, что первый элемент полученного вектора представляет собой произведение первой строки матрицы A на вектор y (1*1+2*1+3*1=6), второй элемент ‑ произведение второй строки на вектор (3*1+1*1-1*1=3) и третий элемент – произведение третьей строки на вектор (1*1+0*1+1*1=2).

Если же мы попробуем умножить матрицу A на вектор-строку x,

>> A*x

??? Error using ==> mtimes

Inner matrix dimensions must agree.

то MATLAB напомнит нам, что умножение матриц возможно только тогда, когда количество столбцов первого сомножителя равно количеству строк второго (Inner matrix dimensions must agree – внутренние размеры матриц должны быть согласованы).

Упражнения.

1. Создайте матрицу .

2. Создайте вектор строку lin и вектор-столбец col

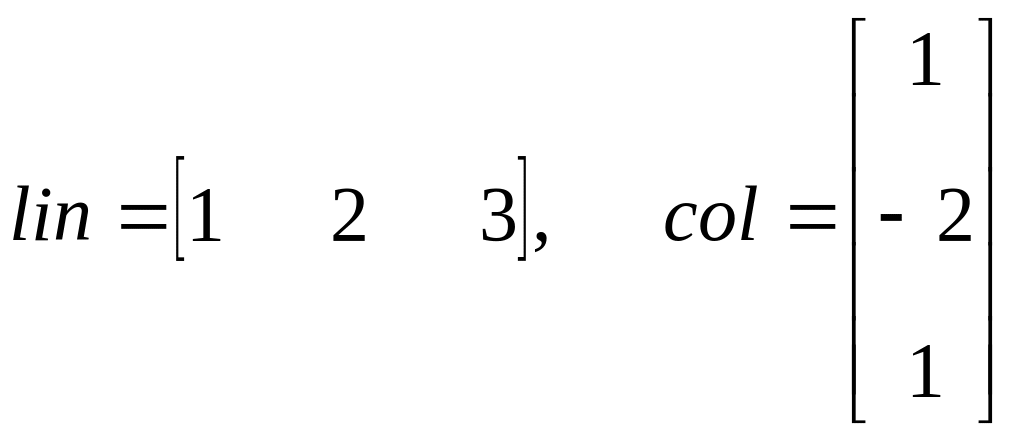
3. Вычислите произведение матрицы A на вектор-столбец col ( Ответ - ).

4. Вычислите значение билинейной формы (-5).

1.3. Построение графиков – функция plot

В предыдущем пункте мы уже увидели преимущества матричной ориентированности MATLAB’а. В других языках для записи матричных операций требуется использовать подпрограммы. Здесь же эти операции записываются (и выполняются) очень просто – так же как они записываются для простых переменных.

Очень просто в MATLAB’е удается получить и графическое представление результатов.

Сейчас мы рассмотрим функцию plot – функцию построения двумерных графиков. В простейшем варианте эта функция использует два аргумента – два вектора с одинаковым количество элементов. В первый вектор следует занести абсциссы, а во второй – ординаты точек графика. Заданные точки соединяются ломаной линией. Пример.

>> x = [0 1 2 3 4 5];

>> y = [1 2 2.5 2.7 2.8 2.9];

>> plot(x,y)

В результате MATLAB покажет вам графическое окно (Figure - фигуру) с заказанным графиком.

К стати, в этом примере есть еще одно небольшое новшество. Команды задания векторов x и y заканчиваются точкой с запятой (;). Точку с запятой ставьте тогда, когда вы хотите подавить эхо-печать – автоматический вывод результата в командное окно.

Однако вводить такие вектора вручную, когда вы хотите построить график с большим количеством точек, занятие не слишком веселое. В таких случаях очень полезна функция – linspace. Эта функция делит числовой отрезок на отрезки равной длины и в качестве результата возвращает вектор с координатами точек, осуществляющих это разбиение. Например,

>> x = linspace(1,2,5)

x =

1.0000 1.2500 1.5000 1.7500 2.0000

Этой командой мы попросили разбить отрезок с левой границей равной 1, и правой границей равной 2, пятью точками на равные отрезки (то есть на четыре отрезка).

Теперь давайте попробуем вычислить sin(x). С точки зрения школьной математики это абсурд. Аргументом синуса должно быть одно число, а мы пытаемся вычислить синус вектора, то есть нескольких чисел. MATLAB, однако, подобные вольности не смущают. Он просто создает новый вектор и заносит в качестве первого элемента синус x(1), в качестве второго – синус x(2) и так до конца вектора x.

>> y = sin(x)

y =

0.8415 0.9490 0.9975 0.9840 0.9093

Теперь посмотрим, как с помощью этих функций (linspace и plot) можно построить вполне приличный график, совсем не похожий на ломаную линию с последнего рисунка. Выполните следующие три команды:

>> x = linspace(0,2*pi,101);

>> y = sin(x);

>> plot(x,y)

Первая команда создает вектор x с 101 числом, которые делят отрезок на 100 равных участков. Обратите внимание, что в конце команды предусмотрительно поставлена точка с запятой. Благодаря этому отключается эхо-печать, чтобы в командное окно не выводились значения 101 элемента вектора x. Вторая строчка заносит в вектор y соответствующие значения функции sin(x).

В результате график синусоиды выглядит довольно презентабельно. Хотя на самом деле он, по-прежнему, представляет собой ломаную линию, но ее отрезки настолько коротки, что выглядят на экране гладкой кривой.

Упражнение.

1. Постройте графики функций , . Здесь у вас могут возникнуть некоторые проблемы с точками разрыва, областями определения. Поэкспериментируйте. Графики должны выглядеть, если не красиво, то сносно. Цель упражнения – приобрести навыки и некоторую свободу в обращении с функцией plot.

Замечание. Для второго графика потребуется вычислить квадраты элементов вектора . Подробнее о таких операциях будет говориться на следующих занятиях. Здесь только укажем, что для вычисления выражение следует записать так:

y = sqrt(1-x.^2);

То есть перед знаком возведения в степень надо поставить точку, смысл которой будет объяснен позднее.

1.4. М-файл – сценарий

До сих пор мы работали в режиме командной строки. В ответ на приглашение MATLAB’а вводили команду, получали ответ, вводили новую команду и т.д. В такой простоте есть свои достоинства.

Однако такой режим начинает тяготить, если вам требуется выполнить несколько однотипных расчетов, отличающихся только исходными данными. Вы, конечно, знаете, что для выполнения таких повторяющихся расчетов используются программы – файлы с последовательностями команд, хранящиеся где-либо на жестком диске.

Разумеется, и MATLAB оснащен средствами программирования. Здесь рассмотрим простейший вариант программы MATLAB’а –файл-сценарий (script-файл).

Предположим, вам требуется многократно решить следующую задачу: для прямоугольного треугольника заданы длины катетов и . Требуется определить длину гипотенузы и тригонометрические функции угла : .

И мея уже некоторый опыт работы в MATLAB’е, вам нетрудно догадаться, что для решения этой задачи достаточно выполнить следующие четыре команды:

с = sqrt(a^2+b^2)

sn = b/c

cs = a/c

tg = sn/cs

Чтобы не набирать заново эти строчки каждый раз для нового варианта данных, создадим файл, содержащий эти команды. Лучше всего использовать для этого встроенный редактор MATLAB’а. Вызвать этот редактор можно любым из следующих способов:

1. набрать в командной строке команду edit;

2. выполнить из меню команду File – New – M-file;

3. нажать на кнопку создания нового файла .

В любом случае на экране появится окно редактора. Давайте занесем в него текст команд, как на рисунке. Обратите внимание, что первая строчка, выделенная зеленым цветом, не содержит никакой команды, а только поясняющий текст – комментарии. MATLAB распознает комментарий по символу процента (%). Весь последующий текст MATLAB при выполнении файла игнорирует.

Тем не менее, комментарии в программировании играют очень важную роль. Вот только предназначены они в отличие команд не для компьютера, а для вас. Они позволят вам даже спустя несколько месяцев легко вспомнить для чего предназначена программа, как она работает. Подробнее о роли комментариев нам еще предстоит поговорить в главе «Техника программирования», а пока что советую приобрести привычку сопровождать комментариями даже очень короткие файлы с программами.

Набрав текст программы (script-файла), следует его сохранить на диске. Как обычно это делается с помощью команды File-Save. Можно, конечно, и просто нажать кнопку на линейке инструментов.

Назовем наш первый script-файл triangle.m. Расширение .m MATLAB по умолчанию использует для файлов с текстами программ, а само имя (triangle) вы выбираете сами. Конечно, лучше выбирать имя, напоминающее о назначении файла.

Достаточно важный вопрос о том, где именно следует сохранить файл, рассмотрим в следующем пункте. А пока что воспользуемся вариантом, предлагаемым MATLAB’ом по умолчанию – сохраним файл в папке work (рабочая).

П осле этого мы можем попросить MATLAB выполнить этот script-файл. Для этого сначала надо задать значения переменных a и b, которые используется в командах файла и, затем, в ответ на очередное приглашение набрать имя файла.

>> a=4;

>> b=3;

>> triangle

c =

5

sn =

0.6000

cs =

0.8000

tg =

0.7500

На этом примере вы убедились, что, встретив в командной строке имя script-файла, MATLAB просто последовательно выполняет команды, содержащиеся в этом файле, точно так же, как если бы они набирались с клавиатуры.

Script-файл – это самая простая возможность создавать программы в MATLAB’е. Позже мы познакомимся с гораздо более гибким и мощным средством – файлами-функциями.

Замечание. М-файлы можно создавать и с помощью любого другого текстового редактора (например, Блокнота), но редактор MATLAB’а предназначен именно для написания и отладки М-файлов, и поэтому имеет ряд преимуществ перед редакторами общего назначения. Например, выделение разными цветами зарезервированных слов, комментариев, символьных строк; средства для непосредственного запуска и отладки М-файлов т.п.

Упражнение.

1. Создайте script-файл для решения квадратного уравнения . Попробуйте решить с его использованием уравнения , , .