3. Формула полной вероятности.

Пусть некоторое событие А может произойти вместе с одним из несовместных событий , составляющих полную группу событий. Пусть известны вероятности этих событий и условные вероятности наступления события А при наступлении события H_i

.

Вероятность события А, которое может произойти вместе с одним из событий , равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.

Фактически эта формула полной вероятности уже использовалась при решении примеров, приведенных выше, например, в задаче с револьвером.

Пример8. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза.

Вероятность того, что выстрелы производит первый, второй или третий стрелок равна .

Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:

- для первого стрелка:

- для второго стрелка:

- для третьего стрелка:

Искомая вероятность равна:

4. Формула Байеса.

С формулой полной вероятности тесно связана формула Байеса. Если до опыта вероятности гипотез были , , ..., , а в результате опыта появилось событие , то с учетом этого события "новые", т.е. условные вероятности гипотез вычисляются по формуле Байеса

Где

Формула Байеса дает возможность "пересмотреть" вероятность гипотез с учетом наблюдавшегося результата опыта.

Пример 9. На заводе, изготовляющем болты, первая машина производит 25%, вторая - 35%, третья - 40% всех изделий. В их продукции брак составляет соответственно 5, 4 и 2%. а) Какова вероятность того, что случайно выбранный болт дефектный? б) Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой, второй, третьей машиной?

Решение. Пусть событие = {выбран дефектный болт}.

Выдвигаем три гипотезы:

={болт изготовлен первой машиной}, =0,25, =0,05;

={болт изготовлен второй машиной}, =0,35, =0,04;

={болт изготовлен третьей машиной}, =0,4, =0,02.

а)

б)

Пример 10. Студент подготовил к экзамену 20 билетов из 25. В каком случае шансы взять известный билет больше - когда студент пришел на экзамен первым или вторым?

Решение.  Найдем вероятность взять известный билет, придя на экзамен вторым, учитывая, что первый может взять как известный, так и неизвестный второму билет.

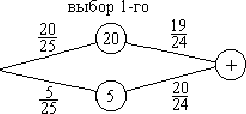
5. Примеры, рекомендуемые для домашнего задания.

1. Для сигнализации об аварии установлены три независимо работающие прибора. Вероятность того, что при аварии сработает первый прибор, равна – 0,9; второй – 0,95; третий – 0,85. Найти вероятность того, что при аварии сработает: А) только один прибор; Б) только два прибора; В) все три прибора.

2. Три стрелка делают по одному выстрелу по одной и той же цели. Вероятность попасть в цель у первого стрелка равна 0,9; у второго – 0,8; у третьего – 0,7. Найти вероятность того, что: а) все стрелки попадут в цель; б) только один стрелок попадет в цель; в) хотя бы один стрелок попадет в цель.

3. Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах равна 0,875. Найти вероятность попадания при одном выстреле.

4. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого и 0,9 для второго сигнализатора. Найти вероятность того, что при аварии сработает только одни сигнализатор.

5. На стеллаже библиотеки в случайном порядке расставлены 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу 3 учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.

6. В урне 12 шаров, из которых 5 белых. Вынимают подряд три шара, не возвращая их. Найти вероятность того, что все три шара окажутся белыми.

7. За один час автомат изготовляет 20 деталей. За сколько часов вероятность изготовления хотя бы одной бракованной детали будет не менее 0,952, если вероятность того, что любая деталь бракованная, равна 0,01?.

8. Игра проводится до выигрыша одним из игроков двух партий подряд. Вероятность выигрыша партии каждым игроком равна 0,5 и не зависит от исходов предыдущих партий. Найти вероятность того, что игра окончится до восьмой партии.

9. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.

10. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.

а) Каков процент брака на конвейере?

б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?

11. Из 40 деталей 10 изготовлены в первом цехе, 25 - во втором, а остальные - в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех - с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?

12. Имеются три одинаковые урны с шарами. В первой из них 3 белых и 4 черных шара, во второй – 2 белых и 5 черных, в третьей – 10 черных шаров. Из случайно выбранной урны наудачу вынут шар. Найти вероятность того, что он белый.

13. Прибор может работать в двух режимах: 1) нормальном и 2) ненормальном. Нормальный режим наблюдается в 80% случаях работы прибора; ненормальный – в 20%. Вероятность выхода прибора из строя за время в нормальном режиме равна 0,1; в ненормальном - 0,7. Найти полную вероятность выхода прибора из строя за время .

14. В пирамиде установлено 9 винтовок из которых 3 снабжены оптическим прицелов вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом равна 0,95, а без оптического прицела 0,5. Найти вероятность того, что цель будет поражена.

15. Три стрелка стреляют по одной мишени. Вероятность попадания для каждого из них соответственно равняют 0,7; 0,8 и 0,9. После залпа в мишени выявили 2 попадания. Найти вероятность того, что в мишень попал первый и третий стрелки.

16. Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6; 0,5; 0,4.

17. На сборку от первой фирмы приходит 65%, со второй 15%, а с третей 20% таких же изделий. На первой фирме брак 2%, на второй 7%, на третей 8%. Наудачу взятая деталь оказалась бракованной. Найти вероятность этого события. Найти вероятность того, что эта деталь пришла из первой фирмы.