5.4.4. Электростатические системы управления электронным лучом.

Пучки заряженных частиц можно не только фокусировать в электростатических полях, но также отклонять, изменять их диаметр и определять их скорость.

Простейшим элементом для управления электронными пучками является плоский конденсатор (рис. 12.4). Электростатическое поле внутри такого конденсатора однородно. Однако вблизи его краев поле становится слабее и изгибается (рис. 12.4) в окружающее пространство, поскольку теоретически поле исчезает только на бесконечном расстоянии от конденсатора. Если расстояние между обкладками конденсатора равно (d), то поле внутри конденсатора можно считать практически однородным до этого расстояния от края. Таким образом, реальный конденсатор можно заменить идеальным с эффективной длиной, несколько большей, чем реальная длина l. Хотя такой идеальный конденсатор не реализуем, поскольку однородное поле не может внезапно исчезнуть, однако такая простая модель является хорошим приближением при описании реального прибора.

Наиболее важным практическим применением плоского конденсатора в электронной и ионной оптике является его использование для отклонения заряженных частиц образующих электронный луч.

При вхождении в конденсатор электронов, образующих пучок, со скоростью:

, (25.4)

где U_a ускоряющая разность потенциалов в промежутке катод – анод, на электроны начинает действовать кулоновская сила: со стороны электростатического поля конденсатора F=eE, направленная перпендикулярно к вектору начальной скорости. Под действием этой силы вектор скорости изменяет направление, и электроны начинают участвовать в двух видах движения. Равномерном, со скоростью V_z, вдоль оси (z) и равноускоренным со скоростью V_y вдоль оси (Y) (рис. 13.4). Уравнение движения для электронов (слагающих пучок) вдоль оси Y:

= , (26.4)

где Е - напряженность поля конденсатора, U – разность потенциалов на обкладках, d – расстояние между пластинами конденсатора. После двукратного интегрирования получим уравнение:

, (27.4)

в котором, исходя из начальных условий, постоянные интегрирования С₁=С₂=0.

Рис. 12.4. Электростатическое поле плоского конденсатора.

Рис.13.4. Траектория электронного луча в электростатическом поле плоского конденсатора.

Подставляя в (27.4) время прохождения электронами в пространстве конденсатора расстояния (l) при скорости движения определяемой равенством (25.4) получим уравнение:

, (28.4)

определяющее величину отклонения электронного пучка от оси z при выходе из конденсатора. Электроны, выйдя из конденсатора, продолжают двигаться по прямой (рис.13.4) направленной под углом  к оси z, а, следовательно, тангенс угла отклонения определится как:

. (29.4)

Величина отклонения электронов (D рис. 13.4), образующих пучок, в плоскости экрана от оси (z) определяется равенством:

D=Y₁+L tg, (30.4.)

после подстановки в которое (29.4) получим:

. (31.4)

Для характеристики отклоняющей системы электронно-лучевых приборов вводится понятие чувствительности электронно-лучевой трубки, которая определяется величиной отношения:

= . (32.4)

Из выражения (32.4) следует, что чувствительность трубки не зависит от заряда частицы. Ни величина отклонения, ни наклон траектории не зависят от отношения заряда к массе частицы. Электроны либо ионы разных масс отклоняются на одну и ту же величину, если они ускорены одинаковым напряжением (хотя скорости сами по себе различны для частиц разной массы, формула 25.4).

Таким образом, одна и та же электростатическая отклоняющая система может быть использована для любой заряженной частицы, что очень удобно при работе с ионными пучками.

Для увеличения чувствительности необходимо:

Рис.14.4. Форма отклоняющих пластин.

1. Уменьшать ускоряющее напряжение U_a, но это приведет к уменьшению яркости пучка.

2, Увеличивать длину пластин конденсатора (l), но при этом увеличиваются размеры трубки.

3. Увеличивать длину пластин (l) и уменьшать расстояние (d) между ними. Однако такой вариант приемлем при условии, чтобы при максимальном отклонении электронный луч не попадал на пластины. Поэтому на практике часто применяют пластины с отогнутыми краями (рис. 14.4). В современных электростатических лучевых трубках чувствительность составляет 0,1 – 0,2 мм/В.

В электронно лучевых трубках для управления пучком электронов обычно используют две пары пластин, разделенных и повернутых по отношению друг к другу на 90⁰ относительно оптической оси (z) (рис.15.4).

Однако в некоторых случаях более удобным, оказывается, использовать большее число простых электродов, поддерживающих соответствующие потенциалы для получения любой конфигурации электростатического поля. На рис.16.4 показано, как расположить восемь электродов, чтобы получить два взаимных перпендикулярных дипольных поля. Это так называемый «октупольный дефлектор».

Такое расположение электродов обладает несколькими преимуществами при сравнении с двумя парами пластин, разделенных и повернутых по отношению друг к другу на 90⁰ относительно оптической оси (z).

Рис.15.4. Отклоняющая система из

двух плоских конденсаторов.

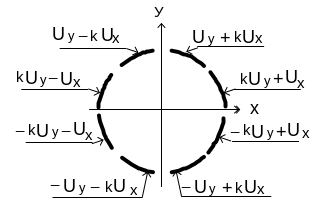
Рис. 16.4. Электростатический

октупольный дефлектор.

1. Оно более компактно и имеет меньшие аберрации. 2). Может быть использовано одновременно как стигматор. 3) Это поле легче вычисляется, чем поле от плоских конденсаторов.

Соотношение между потенциалами электродов, необходимых для надлежащего действия восьми электродного отклоняющего устройства (дефлектора)

Рис. 17.4. Фокусировка пучка заряженных частиц в

электростатическом поле цилиндрического конденсатора.

представлены на рис. 16.4. Символами U_x и U_y обозначены потенциалы, используемые для отклонения в направлениях х и у соответственно. Результирующие напряжения являются суперпозицией этих двух потенциалов, взвешенных параметром k, который в итоге и определяет распределение потенциала в плоскости х-у (0≤k≤1). Его величина влияет на чувствительность отклонения и аберрации.

Для фокусировки и отклонения плоских пучков более удобным оказывается использование электростатического поля создаваемого цилиндрическим конденсатором (рис. 17.4). В таком поле могут существовать траектории частиц, совпадающие с эквипотенциальными линиями. Для плоского пучка эти траектории представляют собой окружности. Заряженные частицы будут двигаться внутри конденсатора вдоль окружности радиуса R₀, если удовлетворяется условие:

=qE(R_o). (33.4)

В поле цилиндрического конденсатора:

, (34.4)

где постоянная определяется разностью потенциалов U, приложенной между пластинами конденсатора:

, (35.4)

а R₁ и R₂ радиусы пластин.

С учетом (35.4) условие (33.4) можно записать в следующем виде:

. (36.4)

Для заряженных частиц, удовлетворяющих этому условию, любая окружность в пространстве между пластинами конденсатора является возможной траекторией, если начальная скорость частицы направлена вдоль окружности (рис.17.4).

Вывод уравнения траектории заряженных частиц в цилиндрическом конденсаторе базируется на полярных координатах и выходит за рамки настоящего курса программы. В связи с этим отметим только некоторые следствия, вытекающие из получаемого уравнения траектории:

U=U₀sin . (37.4)

Угол отсчитывается от линии ОА (рис. 17.4).

1. Пучок заряженных частиц, источником которого является точка А (рис.17.4), находящаяся внутри конденсатора, будет сфокусирован в точке В после поворота на угол, равный / , т.е. на 127,3⁰.

2. Если разрезать конденсатор по линии ОД (биссектриса угла / ) и удалить его вторую часть, то выходящий из конденсатора пучок будет параллельным. Отсюда следует, что параллельный пучок, входящий в цилиндрический конденсатор, будет сфокусирован после поворота на угол , т.е. на угол 63,6⁰.

В общем случае цилиндрический конденсатор, расположенный на пути заряженного плоского пучка с достаточно малой угловой расходимостью, ведет себя как некоторая комбинация цилиндрической линзы, и призмы поворачивающей пучок. Эти свойства полей рассматриваемого типа широко применяются в масс-спектроскопии, (разделении изотопов).