
IV. Предельные теоремы теории вероятности
4.1 Последовательности независимых событий
Рассмотрим
некоторое вероятностное пространство
(Ω, F,
P).
Будем говорить, что события
![]() независимы,
если для всех m,
независимы,
если для всех m,
![]() ,
и всех
,
и всех
![]()
![]()
![]() .
.
Будем говорить,
что события
![]() образуют последовательность
независимых событий,
если для любых n
события
независимы.
образуют последовательность
независимых событий,
если для любых n
события
независимы.
Если
![]() –
последовательность независимых событий,
то последовательность
–
последовательность независимых событий,
то последовательность
![]() где
где
![]() или
или
![]() ,
также является последовательностью
независимых событий.
,
также является последовательностью
независимых событий.
С каждой
последовательностью событий
![]() можно
связать события
можно
связать события
![]()
и (4.1)
![]()
Первое из событий
(4.1) означает, что для любого n
осуществляется
хотя бы одно из событий
![]() ,
k
= n,
n+1,…
т.е. событие
,
k
= n,
n+1,…
т.е. событие
![]() осуществляется
тогда и только тогда, когда происходит
бесконечное число из событий
.
осуществляется
тогда и только тогда, когда происходит
бесконечное число из событий
.
Второе из событий
(4.1) означает, что существует такое число
n,
что
осуществляются все
события
,
k
= n,
n+1,…
т.е. событие
![]() происходит
тогда и только тогда, когда не происходит
лишь конечное число из событий
.
происходит
тогда и только тогда, когда не происходит
лишь конечное число из событий
.
Теорема 1 (Бореля - Кантелли). Если – последовательность независимых событий, то:

Доказательство.
Первый
случай. Из определения верхнего предела
последовательности следует соотношение
![]() .
Тогда согласно свойствам Р3, Р8 вероятностей
событий получим соотношения
.
Тогда согласно свойствам Р3, Р8 вероятностей
событий получим соотношения
![]() 0
при
0
при
![]() ,
как остаток
сходящегося ряда.
,
как остаток
сходящегося ряда.
Второй случай.
Перейдем к событию
![]() Вычислим вероятность
Вычислим вероятность
![]()
![]() ≤
≤

Отсюда
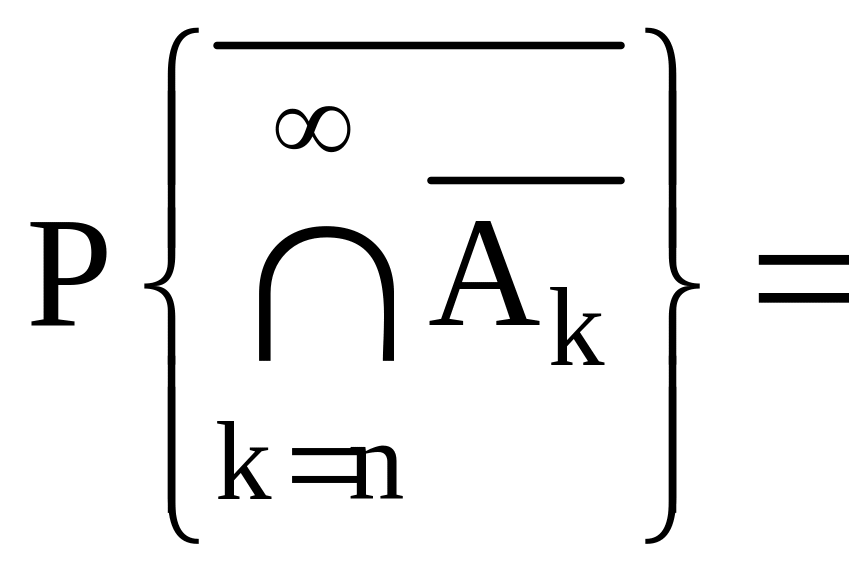 1–
1–![]() →1,
при n→ ∞. Далее,
→1,
при n→ ∞. Далее,
![]() ,
следовательно,
→1,
при n→ ∞. Так как
,
следовательно,
→1,
при n→ ∞. Так как
![]() то
то
![]()
В чем смысл доказанной теоремы? Для независимых событий событие может иметь вероятность 0 или 1. В первом случае это означает что с вероятностью 1 происходит лишь конечное число из событий ; во втором – с вероятностью 1 происходит бесконечное множество событий из .
Замечание. Первый случай теоремы справедлив для любой последовательности событий (необязательно независимых).
4.2. Последовательность независимых величин
Пусть
![]() – последовательность независимых сл.
величин. Это значит, что
– последовательность независимых сл.
величин. Это значит, что
![]() и любых чисел
и любых чисел
![]() события
события
![]() независимы.
независимы.
Замечание. Следует помнить, что когда мы говорим пусть x – сл. величина или пусть – последовательность сл. величин, то полагаем, что существует некоторое вероятностное пространство (W, F, P), на котором эта сл. величина x или эти сл. величины заданы.
Приведем некоторые признаки независимости сл. величин.
Теорема 2. Для
того чтобы сл. величины
![]() были независимы необходимо,
чтобы для любых ограниченных борелевских
функций
были независимы необходимо,
чтобы для любых ограниченных борелевских
функций
![]()
![]() =
=![]() (4.2) и
достаточно,
чтобы равенство (4.2) выполнялось для
непрерывных ограниченных функий.
(4.2) и
достаточно,
чтобы равенство (4.2) выполнялось для
непрерывных ограниченных функий.
Борелевскими называются функции, измеримые относительно s– алгебры борелевских множеств.
Следствие 1. Если
![]() – независимые сл. величины и
– независимые сл. величины и
![]() ,
существуют, то существует и
,
существуют, то существует и
![]() .
.
Следствие 2.
Если
![]() –
независимые сл. величины и
–
независимые сл. величины и
![]() ,
то
–
не коррелированны.
,
то
–
не коррелированны.
Следствие 3.
Если
– независимые сл. величины и
![]() то
то
![]()
Результаты следствий нам уже известны, они приведены в соответствующих свойствах математичского ожидания и дисперсии.
