Интегральное исчисление
Основные понятия и формулы
Неопределенный интеграл. Методы вычисления
Определение
1: Функция
F(x)
называется первообразной
для функции
f(x),
если выполняется равенство
или
.
Определение 2: Совокупность всех первообразных для функции f(x) называется неопределенным интегралом от этой функции и обозначается:
.
Основные свойства неопределенного интеграла:
1.
2.
;
3.
;
4.
.
Таблица интегралов
1.
2.
3.
4.
5.
6.
7.
8.
9.
|
10.
11.
12.
13.
14.
15.
16.
17.
|
Вычисление неопределенного интеграла методом подстановки (замены переменной)
Этот метод
заключается в том, что заменяют переменную
х на
,где
-
непрерывно дифференцируемая функция,
полагают
и получают
.
При этом получают искомую функцию,
выраженную через переменную t.
Для возвращения к переменной х
необходимо заменить t
значением
,
которое находится из соотношения
.
Определенный интеграл и его свойства
Определение
3: Определенным
интегралом от функции
на
отрезке
называется предел интегральной суммы
при условии, что длина наибольшего из
элементарных отрезков стремится к
нулю:
Свойства определенного интеграла
1.
2.
3.
4.
5.
,
Формула
Ньютона-Лейбница
=F(b)-F(a)
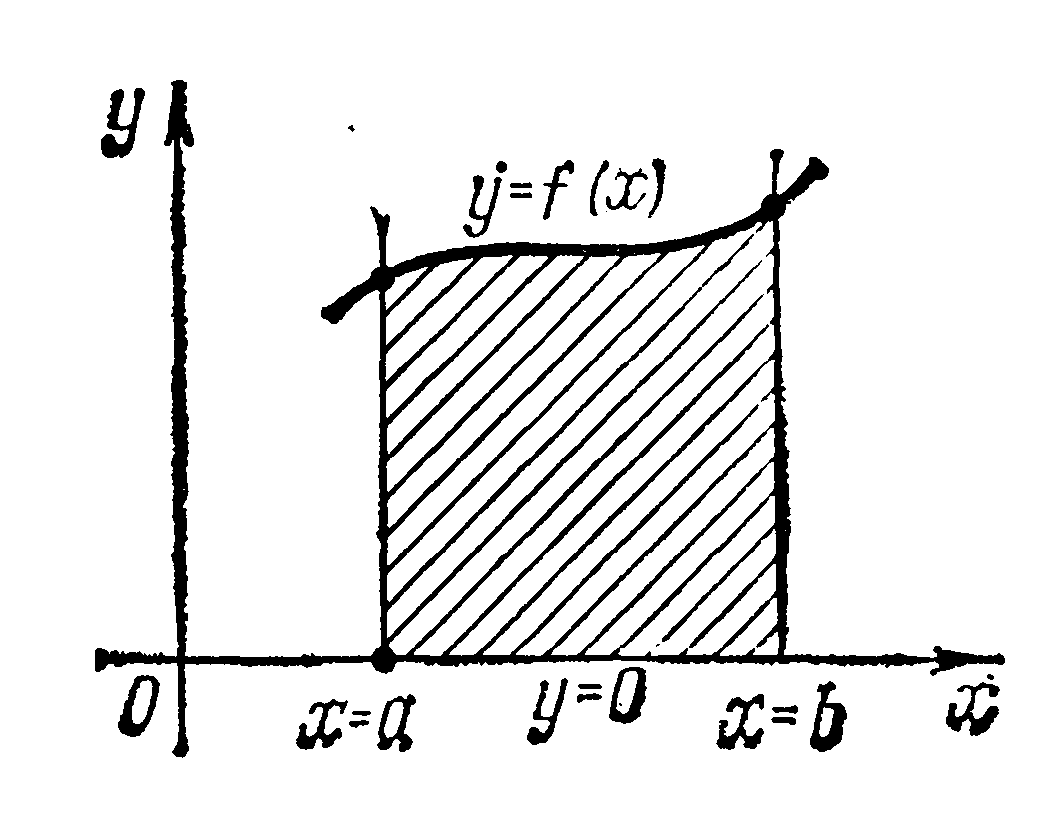
Геометрический смысл определенного интеграла
Если функция на
отрезке
,
то определенный интеграл
геометрически представляет собой
площадь криволинейной трапеции –
фигуры, ограниченной линиями
(
рис.5) Рис.
5
Площадь криволинейной
трапеции, ограниченной кривой
,
прямыми
и отрезком
оси
ОХ, вычисляется по формуле
.
Площадь фигуры,
ограниченной кривыми
,
прямыми
,
вычисляется по формуле
.
Пример 20:
Вычислить неопределенный интеграл
.
Решение:
=
.
Пример 21:
Вычислить неопределенный интеграл
.
Решение:
=
.
Пример 22:
Вычислить неопределенный интеграл
Решение:
=
Пример 23:
Вычислить неопределенный интеграл
Решение:
=
Пример 24:
Вычислить неопределенный интеграл
Решение:
Пример 25:
Вычислить неопределенный интеграл
Решение:
=
Пример 26:
Вычислить определенный интеграл
.
Решение:
=
Пример
27: Вычислить
определенный интеграл:
.
Решение:
.
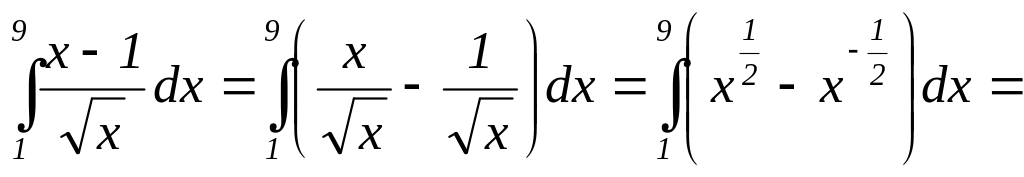
Пример
28: Вычислить
определенный интеграл методом замены
переменной
Решение:
=
=
.
Пример
29: Вычислить
определенный интеграл:
.
Решение:
.
Пример
30: Сделать
чертеж и вычислить площадь фигуры,
ограниченной линиями
.
Решение:
1. Сделаем чертеж.
Графиком
функции
является
парабола, ветви которой направлены
вниз. Найдем координаты вершины параболы:
;
;
.
Вершина параболы
имеет координаты (0;1). Найдем точки
пересечения параболы с осью ОХ:
.
Точки пересечения
с осью ОХ (-1;0) и (1;0).
х |
0 |
1 |
у |
-1 |
0 |
является
прямая. Для построения прямой достаточно
двух точек
Сделаем чертеж (рис.6).
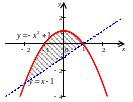
Рис. 6
2. Найдем точки пересечения графиков функции (границы интегрирования). Для этого приравняем функции и решим уравнение
по
теореме Виета
3. Вычислим площадь фигуры ограниченной графиками функций, используя геометрический смысл определенного интеграла.
Ответ:
Площадь фигуры ограниченной линиями
равна 4,5
.
РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
К выполнению контрольной работы следует приступить только после изучения материала, соответствующего данному разделу программы, внимательного ознакомления с примерами решения задач, приведённых в данном пособии по каждой теме.
При выполнении контрольной работы необходимо руководствоваться следующими правилами.
Контрольная работа выполняется в обычной школьной тетради, на обложке которой приводятся следующие сведения: номер контрольной работы, курс, специальность, шифр, ФИО, номер варианта, домашний адрес.
2. В контрольной работе студент должен решить задания того варианта, номер которого совпадает с двумя последними цифрами его шифра. Номера заданий определяются по таблице вариантов.
3. Для замечаний рецензента на страницах тетради оставляются поля шириной 3…4 см. Каждое следующее задание должно начинаться с новой страницы. Условия задач в контрольной работе переписываются полностью без сокращений.
4. Решение должно сопровождаться краткими, но исчерпывающими пояснениями. В тех случаях, когда это, необходимо, дать чертёж, выполненный с помощью чертёжных принадлежностей.
5. В конце контрольной работы следует указать учебники и учебные пособия, которыми пользовались при выполнении работы. Это необходимо для того, чтобы рецензент в случае необходимости мог указать, что следует изучить для завершения контрольной работы.
6. Получив проверенную работу, следует внимательно ознакомиться с замечаниями и указаниями рецензента. Если при выполнении контрольной работы были допущены ошибки, необходимо выполнить работу над ошибками в той же тетради и направить её на повторную проверку. Если повторная работа выполнена в другой тетради, то она обязательно представляется вместе с незачтённой работой.
7. Если при решении отдельных заданий встречаются затруднения, и Вы не можете решить их самостоятельно, то оформите работу, изложив Ваши соображения и затруднения. Такая работа не будет зачтена, но письменная консультация рецензента поможет Вам найти правильное решение.