Теория пределов

Основные понятия и формулы

Определение 1: Число А называется пределом функции y=f(х) при х, стремящемся к а, если для любого сколь угодно малого положительного числа существует такое положительное число , что для всех , удовлетворяющих условию , выполняется неравенство .

Предел функции в точке а обозначается

Основные теоремы о пределах

1.

2.

3.

4.

5.

6.

! Все правила имеют смысл, если пределы функций и существуют.

Замечательные пределы

1. Первый замечательный предел

2. Следствия из первого замечательного предела ,

3. Второй замечательный предел

4. Следствие из второго замечательного предела

Техника вычисления пределов

а) Чтобы раскрыть неопределенность типа , необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной.

б) Чтобы раскрыть неопределенность типа , где под знаком предела стоит рациональная дробь, достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности.

в) Чтобы раскрыть неопределенность типа , если под знаком предела стоит иррациональная дробь, необходимо домножить числитель и знаменатель дроби на сопряженный множитель и сократить множитель приводящий к неопределенности.

г) Необходимо помнить, что

^{, , , , , .}

Пример 1: Вычислить

Решение:

Пример 2: Вычислить

Решение:

Пример 3: Вычислить

Решение:

=

Пример 4: Вычислить

Решение:

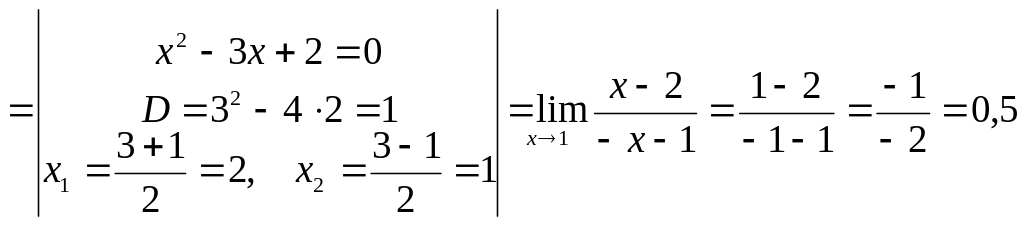
Пример 5: Вычислить

Решение:

Пример 6: Вычислить

Решение:

Пример 7: Вычислить

Решение:

Пример 8: Вычислить

Решение:

Дифференциальное исчисление

Основные понятия и формулы

Определение 1: Производной функции в точке называется предел отношения приращения функции к приращению аргумента , при условии, что приращение аргумента стремится к нулю:

.

Механический смысл производной. Скорость есть первая производная пути по времени, т.е. .

Геометрический смысл производной. Тангенс угла наклона касательной к графику функции равен первой производной этой функции, вычисленной в точке касания, т.е.

Уравнение касательной к графику функции в точке :

Уравнение нормали к графику функции в точке :

Таблица производных

Правила дифференцирования	8. 9. 10. 11. 12. 13. 14. 15. 16.
1. 2. 3. 4. 5. 6. 7.

Определение 2: Дифференциалом функции y=y(x) называется линейная относительно часть приращения функции. Дифференциал функции находится как произведение производной функции на дифференциал независимой переменной:

.

Дифференцирование сложной функции

Пусть y= y(u) , где u= u(x) – дифференцируемые функции. Тогда сложная функция y=y[u(x)] есть также дифференцируемая функция, причем

, или