4 ) Теорема об отрезках пересекающихся хорд.
С
А
B
D
-8-
5
)
l
l – касательная, r – радиус
l
r
и наоборот.
6 ) В
А
АВ = ВС, АВ и ВС - касательные
С
7) В
А
С
,
где АВ
- касательная
L
8 ) С
В
А ВС – касательная, СВА = ВА
9)
A
B
CFD=
C
D
1
0)
D
A B
D
=
C K
-9-
Решение задач по планиметрии. Практикум.
Задача 1.
В окружность
радиуса
вписан
правильный
треугольник АВС. Хорда BD пересекает сторону AC в
точке Е, АЕ : ЕС =3 : 5. Найдите ВЕ.
В Дано:
АВС
– равносторонний,
BD
АС=Е,
АЕ :
ЕС =3 : 5
R=
Найти:
ВЕ
А С
D
Решение:
Способ первый.
1) Так как
АВС
равносторонний,
то все его углы равны по
,
т. е.
,
и все стороны равны, т.е. АВ
= ВС
= АС =
(сторона правильного многоугольника вычисляется по формуле:
Следовательно,
АВ =
ВС = АС
=
.
2) Поскольку АЕ : ЕС =3 : 5, то АЕ=3х, ЕС=5х. Так как АС=8,
АС=АЕ + ЕС =8х, то 8 = 8х, откуда х = 1, значит АЕ=3, ЕС=5.
3) Рассмотрим ЕВС. По теореме косинусов найдем искомую сторону ВЕ.
,
отсюда
ВЕ=7.
Ответ: ВЕ=7.
-10-
Способ второй.
Решение:
1) Так как АВС равносторонний, то все его углы равны по , т. е.
, и все стороны равны, т.е. АВ = ВС = АС = =8.
2) Поскольку АЕ : ЕС =3 : 5, то АЕ=3х, ЕС=5х. Так как АС = 8,
АС=АЕ + ЕС =8х, то 8 = 8х, откуда х = 1, значит АЕ = 3, ЕС = 5.
3) В АВС приведем высоту ВН, причем ВН будет являться высотой и
медианой, т.к. АВС – равносторонний, т.е. АН = НС = 4 (АС = 2НС=8,
отсюда НС=4). Рассмотрим ВНС. ВНС – прямоугольный, поэтому по
теореме Пифагора
4) Рассмотрим
ВНЕ.
ВНЕ
–
прямоугольный,
ВН =
,
ЕН = ЕС – НС = 5 – 4 = 1. Тогда по теореме Пифагора
Ответ: ВЕ = 7.
-11-
Задача 2. Около равнобедренного треугольника с основанием
АС и
углом при основании
описана окружность с
центром О. Найдите её радиус, если площадь
треугольника ВОС равна 16.
В Дано:
АВС
– равнобедренный,
А=
,
16,
ВО=ОС=R
Найти:
R
А С
Решение:
Так как А – вписанный и по условию равен , то дуга ВС, на которую он опирается, равна
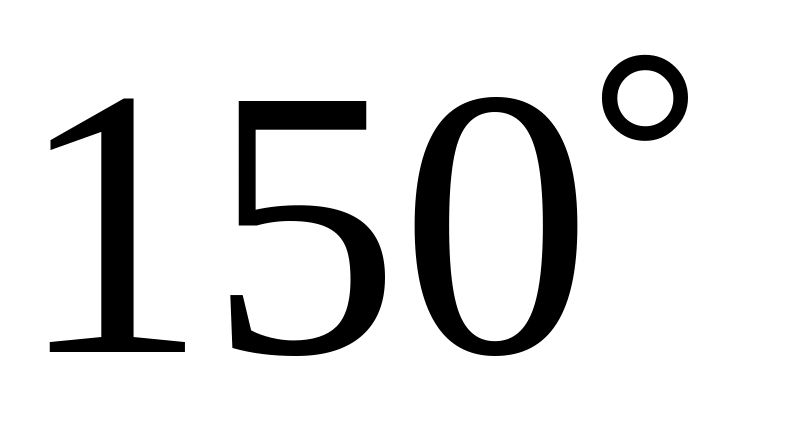(по
определению вписанного угла).
На эту же дугу ВС опирается центральный угол ВОС, тогда
ВОС = .
Рассмотрим ВОС. ВОС – равнобедренный (ВО = ОС как радиусы
одной окружности),
ВОС
=
,
тогда
,
.
По условию
,
тогда 16 =
,
отсюда
,
R
=
8,
но R
= -8 не
удовлетворяет условию задачи, поэтому R = 8.
Ответ: R = 8.
-12-
Задача 3. Из точки А, лежащей на окружности, проведены две
хорды, равные 7 и 15. Найдите диаметр окружности,
если расстояние между серединами хорд равно 10.
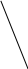
А
Дано:
АВ=15, АС=7
АЕ=ЕВ, AL=LC, EL=10
Найти:
2R
В
С
Решение:
Способ первый.
Выполним дополнительное построение: соединим точки Е и L, В и С и рассмотрим АВС. В АВС EL – средняя линия, так как по условию соединяет середины отрезков АВ и АС. Тогда по теореме о средней линии EL = ВС, следовательно, ВС =20.
С одной стороны,
,
где
,
то есть
.
С другой стороны,
,
или
,
отсюда
,
тогда 2R
= 25.
Ответ: 2R = 25.
-13-
Способ второй.
Решение:
Выполним дополнительное построение: соединим точки Е и L, В и С и рассмотрим АВС. В АВС EL – средняя линия, так как по условию соединяет середины отрезков АВ и АС. Тогда по определению средней линии EL = ВС, следовательно, ВС =20.
По теореме косинусов
.
,
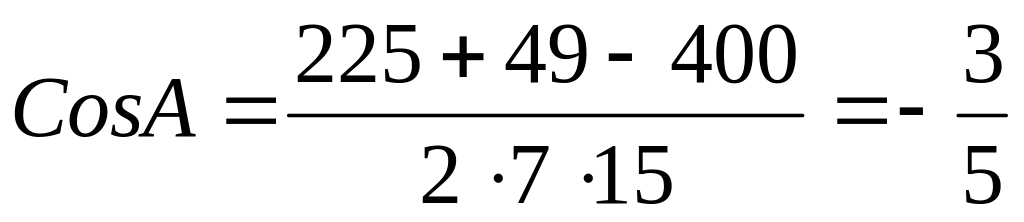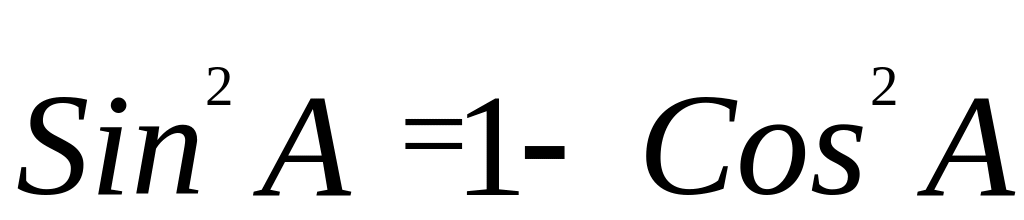тогда
,
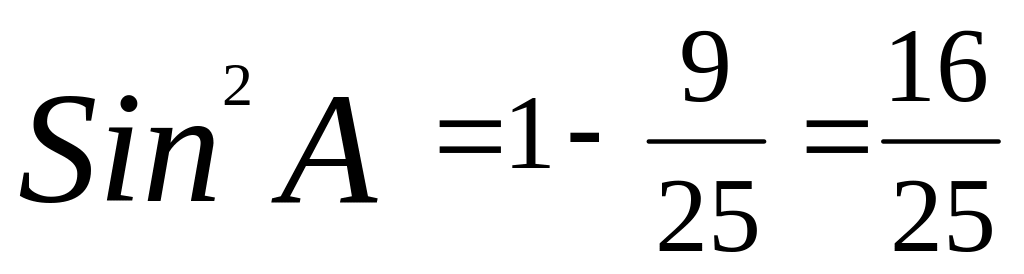отсюда SinА
=
.Из следствия теоремы синусов известно, что
или
,
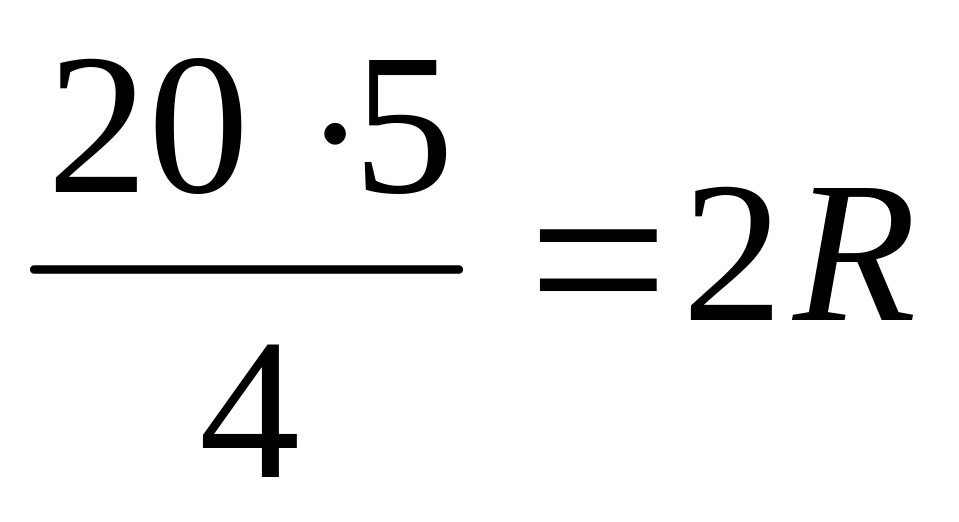откуда 2R
= 25.
Ответ: 2R = 25.
-14-
Задача 4. Найдите радиус окружности, вписанной в
остроугольный треугольник АВС, если высота ВН
равна
12 и известно, что Sin
A
=
Sin
C
=
.
В Дано:
АВС
– остроугольный,
ВН=12,
Sin
A
,
Sin
C
Найти: r
А С
Н
Решение:
1)
АНВ
– прямоугольный, так как ВН
– высота,
поэтому
,
по
условию, тогда
,откуда
АВ
=13.
2)
ВНС
- прямоугольный, так как ВН
– высота,
поэтому
,
по
условию, тогда
,
откуда ВС
= 15.
3)
АНВ:
по теореме Пифагора
,
.
4)
ВНС:
по теореме Пифагора
,
.
5) АС = АН + НС , АС =5 + 9 = 14.
6) С одной стороны,
,
,
с другой стороны,
,
где Р
– периметр, Р
= АВ
+ ВС + АС =13
+ 15 +14 = 42. Тогда
и
,
откуда r
= 4.
Ответ: r = 4.
-15-
Задача 5. В равнобедренный треугольник РМК с основанием
МК
вписана окружность с радиусом
.
Высота
РН
делится точкой пересечения с окружностью в
отношении1 : 2, считая от вершины Р. Найдите
периметр треугольника РМК.
Р
Дано:
РМК – равнобедренный,
r = , РЕ : ЕН = 1 : 2
А
В
РН
- высота
Найти:
М Н К
Решение:
Способ первый.
1) ЕО = ОН = ОВ = ОА= как радиусы одной окружности, причем
ОВ и ОА – радиусы, проведенные в точки касания отрезков МР и РК с
окружностью.
2) ЕН
= ЕО + ОН =
,
по условию,
откуда 2РЕ
= ЕН, РЕ =
3) РВО = РАО по катету и гипотенузе (РО – общая гипотенуза, АО = ОВ),
тогда и РА
= РВ. По
теореме Пифагора
,
,
тогда РВ =
РА = 6.
4) Пусть РК = РМ = х, тогда ВК = АМ = х – 6. Но ВК = НК, АМ = МН, как
отрезки касательных, проведенных из одной точки к окружности.
РНК:
по теореме Пифагора
,
или
,
,
,
откуда х
=12. Тогда РК
= РМ= 12,
МК = МН + НК = 2 НК (так как РМК – равнобедренный, РН – высота и
медиана), или МК = 2х – 12 = 12.
5)
,
.
Ответ:
.
-16-
Способ второй.
Решение:
1) ЕО = ОН = ОВ = ОА= как радиусы одной окружности, причем
ОВ и ОА – радиусы, проведенные в точки касания МР и РК с окружностью.
2) ЕН = ЕО + ОН = , по условию, откуда 2РЕ = ЕН, РЕ = ,
тогда РО
= РЕ + ЕО =
+
=
,
РН
= РО + ЕН =
+
=
.
3) РВО = РАО по катету и гипотенузе (РО – общая гипотенуза, АО = ОВ),
тогда и РА
= РВ и
ОРВ =
ОРА.
РВО:
,
значит,
ОРВ =
ОРА
=
.
4)
РНК
:
,
НРК
=
ОРВ
=
,
,
значит,
,
откуда РК
= РМ
= 12.
5)
РКМ
=
РМК
=
(из
РНК
:
),
как углы при
основании равнобедренного треугольника. Тогда МРК = (из РМК:
),
следовательно,
РНК
– равносторонний и МК=12.
6) , .
Ответ: .
-17-
Задача 6. Один из катетов прямоугольного треугольника равен