
- •Теория вероятностей и математическая статистика
- •Предисловие
- •Рабочая программа Модуль 1 Случайные события. Вероятность события
- •Рекомендуемая литература
- •Дополнительная литература
- •Модуль 0 Введение
- •Модуль 1 Случайные события. Вероятность события
- •§ 1 Случайные события
- •§ 2 Виды случайных событий
- •§ 3 Вероятность события
- •§ 4 Элементы комбинаторики
- •Модуль 2 Основные теоремы теории вероятностей
- •§ 1 Действия над событиями
- •§ 2 Теоремы сложения вероятностей
- •§ 3 Теоремы умножения вероятностей
- •Все 3 саженца выдержат испытание,
- •Хотя бы один из саженцев выдержит испытание,
- •Не менее двух саженцев выдержат испытание?
- •§ 4 Формула полной вероятности. Формула Байеса
- •Модуль 3
- •§ 1 Формула Бернулли
- •§ 2 Формула Пуассона
- •§ 3 Локальная теорема Лапласа
- •§ 4 Интегральная теорема Лапласа
- •§ 5 Наивероятнейшее число наступлений события при повторении испытаний
- •§ 1 Дискретные и непрерывные случайные величины.
- •§ 2 Числовые характеристики случайных величин
- •Модуль 5 Основные законы распределения случайных Величин
- •§ 1 Биномиальный закон распределения
- •§ 2 Закон Пуассона
- •§ 3 Равномерный закон распределения
- •§ 4 Показательный закон распределения
- •§ 5 Нормальный закон распределения
- •§ 6 Функция надежности
- •Модуль 6 Системы случайных величин
- •§ 1 Системы случайных величин
- •§ 2 Ковариация и корреляция
- •§ 3 Функции случайных величин
- •Модуль 7 Закон больших чисел и локальные предельные теоремы
- •§ 1 Неравенство Чебышева
- •§ 2 Закон больших чисел в форме Чебышева
- •§ 3 Теорема Бернулли
- •§ 4 Усиленный закон больших чисел
- •Модуль 8 Элементы математической статистики
- •§ 1 Выборочный метод
- •§ 2 Эмпирическая функция распределения
- •§ 3 Полигон и гистограмма
- •Модуль 9 Статистические оценки параметров распределения
- •§ 1 Точечные оценки
- •§ 2 Интервальные оценки
- •§ 3 Отыскание параметров уравнения прямой линии по опытным данным. Метод наименьших квадратов
- •§ 4 Вычисление выборочного коэффициента корреляции
- •Методические указания к выполнению контрольной работы
- •Задания КонтрольнОй работЫ
- •Решение варианта «a»
- •2) Коэффициент корреляции r;
- •3) Уравнение прямой регрессии y на х ;
- •4) Построить корреляционное поле и график регрессии y на х.
- •Справочный материал Случайные события
- •Случайные величины
- •Элементы математической статистики
- •Приложения
- •Значения , определяемые уравнением
- •Содержание
§ 1 Дискретные и непрерывные случайные величины.
Функции распределения случайной величины
Определение 1.
Случайной называется величина, которая в результате опыта может принять одно, и только одно, возможное значение, неизвестно заранее, какое именно.
Например, посеяно 100 зерен пшеницы для определения ее всхожести. Число взошедших зерен есть случайная величина, которая может принять одно из значений: 0, 1, 2, …, 100.
Определение 2.
Случайная величина называется дискретной, если она принимает отдельные, изолированные друг от друга возможные значения, которые можно перенумеровать.
Число взошедших зерен пшеницы есть дискретная случайная величина.
Определение 3.
Непрерывной случайной величиной называется такая, случайная величина возможные значения которой, непрерывно заполняют какой-то промежуток, конечный или бесконечный.
Например,
расстояние, которое пролетит снаряд
при выстреле из оружия, есть непрерывная
случайная величина. Возможные значения
этой величины принадлежат некоторому
промежутку

Случайные
величины обозначаются:
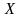 ,
,
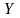 ,
,
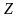 и т.д.
и т.д.
Определение 4.
Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Для дискретной случайной величины закон распределения можно задать в виде таблицы
|
|
|
|
… |
|
|
|
|
|
… |
|
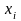 — возможные
значения случайной величины
,
— возможные
значения случайной величины
,
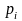 — соответствующие
им вероятности.
— соответствующие
им вероятности.
Причем
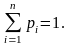
Определение 5.
Интегральной
функцией распределения
случайной величины
называется функция
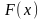 выражающая вероятность того, что
случайная величина
примет значение, меньшее чем
выражающая вероятность того, что
случайная величина
примет значение, меньшее чем
 :
:
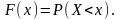
Свойства интегральной функции .
1.
Значения интегральной функции принадлежат
отрезку
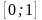 .
.
 .
.
2.
— неубывающая функция, т.е.
 если
если

3.
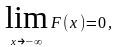
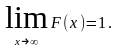
4.
Вероятность того, что случайная величина
примет значение в интервале
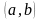 ,
равна приращению интегральной функции
на этом интервале:
,
равна приращению интегральной функции
на этом интервале:
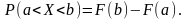
5.
Вероятность того, что непрерывная
случайная величина
примет одно конкретное значение, равна
нулю, т.е.
 Поэтому, для непрерывной случайной
величины справедлива формула
Поэтому, для непрерывной случайной
величины справедлива формула

Определение 6.
Дифференциальной
функцией распределения или
плотностью
вероятности случайной величины
в точке
называется отношение вероятности
попадания непрерывной случайной величины
на элементарный участок от
до
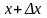 к длине этого участка, когда
к длине этого участка, когда

Обозначается
плотность вероятности через
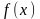 .
По определению имеем:
.
По определению имеем:
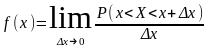 .
.
Так
как
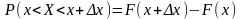 ,
,
то
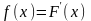 .
.
Таким
образом, если существует
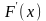 ,
то существует
,
что обычно и предполагают.
,
то существует
,
что обычно и предполагают.
Интегральная функция выражается через дифференциальную формулой:
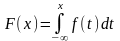 .
.
Свойства дифференциальной функции
1.
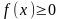 ,
т.е. дифференциальная функция не
отрицательна.
,
т.е. дифференциальная функция не
отрицательна.
2.
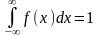 .
Вероятность того, что случайная величина
примет значение, принадлежащее интервалу
.
Вероятность того, что случайная величина
примет значение, принадлежащее интервалу
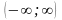 ,
равна единице.
,
равна единице.
3.
Вероятность того, что непрерывная
случайная величина
примет значение в интервале
,
равна определенному интегралу от
дифференциальной функции, взятому в
пределах от
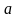 до
до
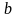 :
:
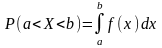 .
.
Геометрически
эта вероятность равна площади
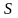 криволинейной трапеции на рисунке 4.1:
криволинейной трапеции на рисунке 4.1:
 f(x)
f(x)









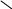

a b х
Рис. 4.1
