Модуль 3

Схема испытаний Бернулли

§ 1 Формула Бернулли

Теорема. Если в каждом из 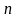независимых испытаний вероятность появления события А постоянна и равна , то вероятность того, что в независимых испытаниях событие А наступит раз, определяется по формуле Бернулли.

, где .

На практике формулой Бернулли удобно пользоваться, если — не очень велико .

§ 2 Формула Пуассона

Теорема. Если производится достаточно большое число испытаний ( — велико), в каждом из которых вероятность наступления события А постоянна, но мала, то вероятность того, что в испытаниях событие А наступит раз, определяется приближенно формулой

, где .

§ 3 Локальная теорема Лапласа

Теорема. Если производится независимых испытаний ( — велико), и вероятность наступления события А в каждом испытании постоянна и равна , то вероятность того, что в независимых испытаниях событие А наступит раз, определяется по формуле

,

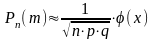где , ,

причем результат тем точнее, чем ближе значение к 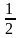и больше .

Функция 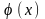— четная. Значения функции находятся по таблице "Приложение №1", помещенной в конце методических указаний. Для 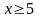полагают

§ 4 Интегральная теорема Лапласа

Теорема. Если вероятность наступления события А в каждом из независимых испытаний постоянна и отлична от нуля и единицы, то вероятность того, что в независимых испытаниях событие А наступит не менее чем 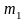раз и не более чем 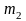раза, определяется по формуле

,

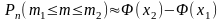где ,

, .

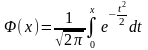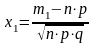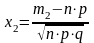Функция 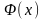— нечетная. Значения находятся по таблице Приложения 2, помещенной в конце данного пособия. Для полагают

§ 5 Наивероятнейшее число наступлений события при повторении испытаний

Наивероятнейшим числом 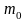появления события А в независимых испытаниях называется число, для которого вероятность 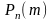превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных исходов испытаний.

Наивероятнейшее число определяется по формуле

,

где — число независимых испытаний;

— вероятность наступления события А в одном испытании;

— вероятность не наступления события А в одном испытании;

— наивероятнейшее число наступлений событий А.

Пример 3.1.

Всхожесть семян данного растения составляет 90% . Найти вероятность того, что из пяти посеянных семян взойдут:

а) четыре; б) не менее четырёх.

Решение.

Воспользуемся формулой Бернулли. Если производится n независимых испытаний, при каждом из которых вероятность осуществления события А постоянна и равна p, а вероятность противоположного события равна q = 1 - p, то вероятность того, что при этом событии А осуществляется ровно m раз, вычисляется по формуле

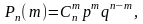
где 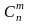— число сочетаний из n элементов по m.

а) По условию задачи вероятность всхожести семян р = 0,9;

тогда q = 0,1; в данном случае n = 5 и m = 4. Подставляя эти данные в формулу Бернулли , получим

б) Искомое событие А состоит в том, что из пяти посеянных семян взойдут или четыре, или пять. Таким образом, Первое слагаемое уже найдено. Для вычисления второго снова применяем формулу Бернулли:

Следовательно,

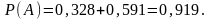
Пример 3.2.

Вероятность наступления некоторого события при одном испытании равна 0,3. Найти вероятность того, что при 100 испытаниях:

а) событие появится 28 раз;

б) событие появится не менее 25 и не более 32 раз.

Решение.

а) Воспользуемся локальной теоремой Лапласа.

Здесь ;

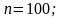
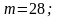
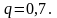
где 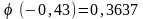найдено по таблице Приложения 1

б) Воспользуемся интегральной теоремой Лапласа

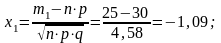
Значения 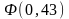и 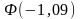найдены по таблице Приложения 2

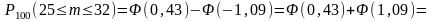
Задача 3.3.

Пусть известно, что на выпечку 1000 сдобных булочек с изюмом полагается изюмин. Найти вероятность того, что в купленной булочке будет: а) не менее 7 и не более 10 изюмин; б) ни одной изюмины.

Решение.

Покупку булочки в магазине можно рассматривать как случайный выбор. Ясно, что при хорошем перемешивании теста с изюмом отдельные изюмины распределятся в нем статистически равномерно. Поскольку всего 1000 булочек, то вероятность каждой изюмины попасть в выбранную булочку есть Условие статистической равномерности распределения изюмин и независимости числа изюмин в каждой булочке можно считать практически выполненным. Условие тоже приближенно выполняется:

или

Следовательно, имеется возможность применения формулы Пуассона.

Величина - среднее число изюмин, приходящихся на одну булочку.

а) Вероятность того, что

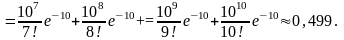
б) Вероятность купить булочку вовсе без изюма

ЧТО ДОЛЖЕН ЗНАТЬ СТУДЕНТ

1. Схема испытаний Бернулли.

2. Формула Бернулли.

3. Формула Пуассона.

4. Локальная теорема Лапласа.

5. Интегральная теорема Лапласа.

6. Наивероятнейшее число наступивших событий в схеме Бернулли.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Четыре покупателя приехали на оптовый склад. Вероятность того, что каждому покупателю потребуется холодильник марки А, равна 0,4. Найти вероятность того, что холодильник потребуется: двум покупателям; не менее чем двум покупателям; не более чем трем покупателям; всем четырем покупателям.

2. Завод отправил в торговую сеть 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что при транспортировке будет повреждено: ровно три изделия; более трех изделий.

3. Станок автомат делает детали. Вероятность того, что деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется ровно 4 бракованных.

4. Вероятность получения отличной оценки на экзамене равна 0,2. Найти наивероятнейшее число отличных оценок и вероятность этого числа, если сдают экзамен 75 студентов.

5. Известно, что 80% специалистов в районе имеет высшее образование. Найти вероятность того, что из 100 наудачу отобранных человек высшее образование имеет: не менее 70; от 65 до 90 человек.

Модуль 4

Случайные величины и их

числовые характеристики