
- •Теория вероятностей и математическая статистика
- •Предисловие
- •Рабочая программа Модуль 1 Случайные события. Вероятность события
- •Рекомендуемая литература
- •Дополнительная литература
- •Модуль 0 Введение
- •Модуль 1 Случайные события. Вероятность события
- •§ 1 Случайные события
- •§ 2 Виды случайных событий
- •§ 3 Вероятность события
- •§ 4 Элементы комбинаторики
- •Модуль 2 Основные теоремы теории вероятностей
- •§ 1 Действия над событиями
- •§ 2 Теоремы сложения вероятностей
- •§ 3 Теоремы умножения вероятностей
- •Все 3 саженца выдержат испытание,
- •Хотя бы один из саженцев выдержит испытание,
- •Не менее двух саженцев выдержат испытание?
- •§ 4 Формула полной вероятности. Формула Байеса
- •Модуль 3
- •§ 1 Формула Бернулли
- •§ 2 Формула Пуассона
- •§ 3 Локальная теорема Лапласа
- •§ 4 Интегральная теорема Лапласа
- •§ 5 Наивероятнейшее число наступлений события при повторении испытаний
- •§ 1 Дискретные и непрерывные случайные величины.
- •§ 2 Числовые характеристики случайных величин
- •Модуль 5 Основные законы распределения случайных Величин
- •§ 1 Биномиальный закон распределения
- •§ 2 Закон Пуассона
- •§ 3 Равномерный закон распределения
- •§ 4 Показательный закон распределения
- •§ 5 Нормальный закон распределения
- •§ 6 Функция надежности
- •Модуль 6 Системы случайных величин
- •§ 1 Системы случайных величин
- •§ 2 Ковариация и корреляция
- •§ 3 Функции случайных величин
- •Модуль 7 Закон больших чисел и локальные предельные теоремы
- •§ 1 Неравенство Чебышева
- •§ 2 Закон больших чисел в форме Чебышева
- •§ 3 Теорема Бернулли
- •§ 4 Усиленный закон больших чисел
- •Модуль 8 Элементы математической статистики
- •§ 1 Выборочный метод
- •§ 2 Эмпирическая функция распределения
- •§ 3 Полигон и гистограмма
- •Модуль 9 Статистические оценки параметров распределения
- •§ 1 Точечные оценки
- •§ 2 Интервальные оценки
- •§ 3 Отыскание параметров уравнения прямой линии по опытным данным. Метод наименьших квадратов
- •§ 4 Вычисление выборочного коэффициента корреляции
- •Методические указания к выполнению контрольной работы
- •Задания КонтрольнОй работЫ
- •Решение варианта «a»
- •2) Коэффициент корреляции r;
- •3) Уравнение прямой регрессии y на х ;
- •4) Построить корреляционное поле и график регрессии y на х.
- •Справочный материал Случайные события
- •Случайные величины
- •Элементы математической статистики
- •Приложения
- •Значения , определяемые уравнением
- •Содержание
2) Коэффициент корреляции r;
3) Уравнение прямой регрессии y на х ;
4) Построить корреляционное поле и график регрессии y на х.
Х |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Y |
2 |
1,9 |
2,2 |
2,4 |
2,3 |
2,5 |
2,5 |
Решение. Для вычислений составим таблицу
i |
xi |
yi |
xi2 |
yi2 |
xi yi |
1 |
2 |
2 |
4 |
4 |
4 |
2 |
3 |
1,9 |
9 |
3,61 |
5,7 |
3 |
4 |
2,2 |
16 |
4,84 |
8,8 |
4 |
5 |
2,4 |
25 |
5,76 |
12 |
5 |
6 |
2,3 |
36 |
5,29 |
13,8 |
6 |
7 |
2,5 |
49 |
6,25 |
17,5 |
7 |
8 |
2,5 |
64 |
6,25 |
20 |
å |
35 |
15,8 |
203 |
36 |
81,8 |
1) Находим выборочные средние

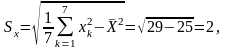

2) Находим коэффициент корреляции по формуле
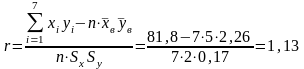 .
.
3)
Для
составления уравнения линейной регрессии
Y
на Х
воспользуемся формулой
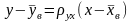 ,
где
,
где

Подставляем полученные результаты в уравнение прямой регрессии и получаем:


4) Построим корреляционное поле и график регрессии Y на X:

y
 2
2


0 1 2 3 4 5 6 7 8 х
Справочный материал Случайные события
Основные формулы комбинаторики
а)
перестановки

б)
размещения

в)
сочетания

Классическое определение вероятности события

Вероятность суммы событий
а) —
для несовместных
—
для несовместных
б) — для совместных
Вероятность произведения событий
а)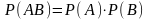 —
для независимых
—
для независимых
б) —
для зависимых
—
для зависимых
Формула полной вероятности

Формула Байеса

Формула Бернули
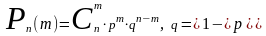
Наивероятнейшее число наступления события

Локальная формула Лапласа

Интегральная формула Лапласа

Случайные величины
Ряд распределения
xi |
x1 |
x2 |
… |
xn |
|
pi |
y1 |
y2 |
… |
yn |
|
где

Функция распределения (интегральная функция)
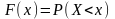
Плотность распределения (дифференциальная функция)
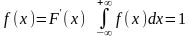
Связь функции распределения с плотностью распределения
Вероятность попадания случайной величины в заданный интервал
а)

б)

Математическое ожидание случайной величины
а)
 —
для дискретной
—
для дискретной
б)
 —
для непрерывной
—
для непрерывной
Дисперсия случайной величины
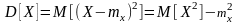
а)
 —
для дискретной
—
для дискретной
б)
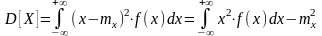 —
для непрерывной
—
для непрерывной
Среднее квадратическое отклонение случайной величины

Начальный момент r – го порядка случайной величины
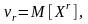 в
частности
в
частности

Центральный момент r – го порядка случайной величины
 ,
в частности
,
в частности
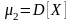
Биноминальное распределение (дискретное)
-
xk
0
1
…
k
…
n
pk
qn
npqn-1

pn


Pk
0,6 P = 0,2 P = 0,8


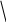 P
=
0,5
P
=
0,5


 0,4
0,4



 0,2
0,2

0 1 2 3 4 k
Пуассоновское распределение (дискретное)
-
xk
0
1
…
k
…
pk
e-a
ae-a
…

…
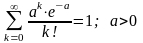

P k
k

0,6 a=0,5



 0,4
a=1
a=5
0,4
a=1
a=5
 0,2
0,2

0 1 2 3 4 5 6 k
23. Показательное распределение (непрерывное)
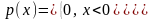
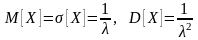
p (х)

 4
λ
= 5
4
λ
= 5
 λ
= 1
λ
= 1
2

 1
2 3 х
1
2 3 х
24. Равномерное распределение (непрерывное)


 p(x)
p(x)
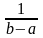



a 0 b x
Нормальное распределение (непрерывное)
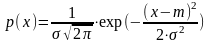

p(x)

 0,8
σ
=
0,5
0,8
σ
=
0,5


 0,4
σ
=
1
0,4
σ
=
1

 σ
=
2
σ
=
2
 m
x
m
x
Функция Лапласа

27. Вероятность попадания нормально распределенной случайной величины Х в заданный интервал ( a, b )

28.Вероятность отклонения нормально распределенной случайной величины Х от ее математического ожидания m на величину d

Асимметрия

30. Эксцесс

31. Вероятность отклонения относительной частоты от постоянной
вероятности на величину e

