Модуль 8 Элементы математической статистики

§ 1 Выборочный метод

Рассмотрим некоторый объект, у которого имеется какой-либо случайный параметр . Например, деталь, которая имеет размер .

Выборочной совокупностью (или выборкой) называется совокупность случайно отобранных объектов. В данном примере — случайно отобранных деталей. Генеральной совокупностью называется совокупность всех объектов, из которых производится выборка. Генеральная и выборочная совокупности характеризуются объемами, которые будем обозначать и соответственно.

Например, если из 500 деталей отобрано 200 для измерения размера , то объем генеральной совокупности 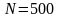, а объем выборки будет .

Допустим, что в выборке случайный параметр принял следующие значения: , , …, , …, .

При этом значение встречалось раз,

встречалось раз,

----------------------------

встречалось раз,

----------------------------

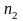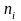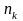встречалось раз.

Очевидно, что .

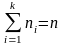В примере с деталью это означает, что размер был зафиксирован раз, размер — раз и т.д.

Наблюдаемые значения случайной величины :

, , …, , …, , называются вариантами. Последовательность вариант, записанных в порядке возрастания, называется вариационным рядом, числа наблюдений вариант называются частотами, а их отношения к объему выборки — относительными частотами .

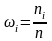Очевидно, что .

Статистическим распределением выборки (или распределением выборки) называют перечень вариант вариационного ряда и соответствующих им частот или относительных частот .

Пример 8.1.

Выборка в виде распределенных частот:

	2	5	7
	1	3	6

Найти распределение относительных частот.

Решение.

Найдем объем выборки: .

Найдем относительные частоты:

; ; .

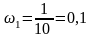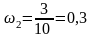Напишем искомое распределение относительных частот:

	2	5	7
	0,1	0,3	0,6

Контроль: .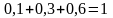

§ 2 Эмпирическая функция распределения

Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения (из возможных значений случайной величины ) относительную частоту события :

,

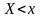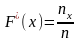где — число вариант меньших ;

— объем выборки.

Эмпирическая функция распределения обладает теми же свойствами, что функция распределения :

1) значения эмпирической функции принадлежат отрезку ;

2) — неубывающая функция;

3) если — наименьшая варианта, а — наибольшая, то

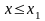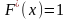при и при .

Пример 8.2.

Найти эмпирическую функцию распределения по данному распределению выборки:

	1	4	6
	10	15	25

Решение.

Найдем объем выборки: .

Наименьшая варианта равна единице, следовательно при .

Значение , а именно , наблюдалось 10 раз, следовательно при .

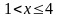Значения 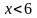, а именно и 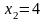, наблюдались 10+15=25 раз, следовательно при .

Так как 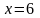— наибольшая варианта, то при .

Напишем искомую эмпирическую функцию распределения:

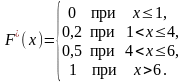
1 4 6 х

Рис.8.1