§ 2 Ковариация и корреляция

Важную роль в теории систем случайных величин играет корреляционный момент (ковариация)

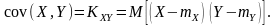
Для дискретных случайных величин корреляционный момент находится по формуле

а для непрерывных

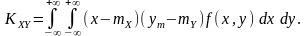
Случайные величины X и Y называются некоррелированными, если их корреляционный момент равен нулю, и коррелированным — в противном случае.

По свойствам математического ожидания

Такое выражение для корреляционного момента иногда удобнее для вычислений, и отсюда следует, что независимые случайные величины некоррелированы.

Если корреляционный момент положителен, то случайные величины называются положительно коррелированными, если отрицателен — то отрицательно коррелированными.

Вместо корреляционного момента часто используется коэффициент корреляции

являющийся безразмерной величиной.

Если случайные величины X и Y связаны точной линейной зависимостью то , т.е. при и при .

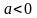Легко видеть, что коэффициент корреляции удовлетворяет условию

Пример 6.2. Найти коэффициент корреляции для случайных величин X ,Y из примера 6.1.

Решение. Найдем M(X Y). Для этого переберем все клетки таблицы, перемножим значения компонент X, Y и вероятности, записанные в этих клетках, и все эти произведения сложим. Тогда 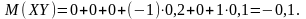Значит, Теперь получаем

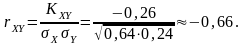
Пусть Закон распределения двумерной случайной величины (X, Y), задаваемый плотностью

,

называют нормальным законом распределения на плоскости. Здесь — параметры этого распределения, вероятностный смысл которых ясен из обозначений.

В случае нормального распределения системы (X, Y) некоррелированность означает независимость случайных величин X, Y. При связаны линейной зависимостью, поэтому значение коэффициента корреляции есть мера линейной зависимости нормально распределенных на плоскости случайных величин X, Y.

§ 3 Функции случайных величин

Пусть Х — случайная величина, а — обычная функция, область определения которой содержит множество значений случайной величины Х. Тогда — случайная величина, являющаяся функцией от случайной величины Х.

Говорят также, что Х есть аргумент функционально зависимой случайной величины Y.

Возникает задача: как, зная распределение случайного аргумента Х, определить закон распределения функции 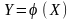? Если Х — дискретная случайная величина, то это сделать нетрудно; а если Х — непрерывная случайная величина, то это сложнее, и на этот счет справедлива следующая теорема.

Теорема. Пусть Х — непрерывная случайная величина с плотность распределения — монотонная дифференцируемая функция; тогда плотность распределения случайной величины есть

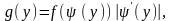
где функция обратная к .

Математическое ожидание случайной величины находится так: ,если случайная величина Х дискретна; 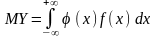, если Х непрерывна и ее плотность есть

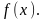
Пример 6.3. За каждый процент перевыполнения плана полагается 40 тыс. руб., а за каждый процент недовыполнения заработок уменьшается на 30 тыс. руб., но не более, чем на 100 тыс. руб. Найти ожидаемый размер премии, если прогноз выполнения плана следующий:

96	97	98	99	100	101	102	103
0,0,1	0,02	0,03	0,2	0,2	0,2	0,2	0,14

Каков ожидаемый размер премии, если известно, что план выполнен?

Решение. Найдем ожидаемый размер премии Y. Это есть функция от процента выполнения плана. К прогнозу выполнения плана снизу пристраиваем еще одну строку значений Y (тыс. руб.)

96	97	98	99	100	101	102	103
0,01	0,02	0,03	0,2	0,2	0,2	0,2	0,14
-100	-90	-60	-30	0	40	80	120

Имеем

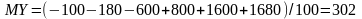тыс. руб.

В заключении отметит, что зависимость между случайными величинами подробно будет рассмотрена позже.

ЧТО ДОЛЖЕН ЗНАТЬ СТУДЕНТ

1. Система двух случайных величин.

2. Числовые характеристики системы двух случайных величин.

3. Корреляционный момент.

4. Коэффициент корреляции.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Имеется таблица распределения двумерной случайной величины (X, Y):

X Y	1	2	3
2	0.07	0.16	0.10
4	0.13	0.09	0.18
6	0.10	0.05	0.12

Составить таблицы распределения вероятностей для каждой из величин X и Y.

2. Для заданного закона распределения вероятностей двумерной случайной величины (X,Y)

Y X	1	4
3	0.12	0.20
5	0.24	0.15
6	0.22	0.07

Найти коэффициент корреляции между величинами X и Y.