§ 6 Функция надежности

Функцией надежности называют функцию, определяющую вероятность безотказной работы элемента за время длительностью :

,

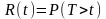где — длительность времени безотказной работы элемента.

Для показательного закона распределения вероятность безотказной работы элемента за время вычисляется по формуле:

.

Пример 5.2.

Автомат изготовляет шарики для подшипника. Шарик считается годным, если отклонение диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная величина распределена нормально, где 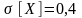мм, найти, сколько в среднем будет годных шариков среди ста изготовленных.

Решение.

Так как — отклонение диаметра от проектного размера, то

. Тогда

.

Таким образом, вероятность того, что диаметр шарика отклонится от проектного меньше чем на 0,7 мм, равна 0,92. Отсюда следует, что примерно 92 шарика из 100 окажутся годными.

ЧТО ДОЛЖЕН ЗНАТЬ СТУДЕНТ

1. Биномиальный закон распределения.

2. Закон Пуассона.

3. Показательный закон распределения.

4. Равномерный закон распределения.

5. Нормальный закон распределения.

6. Функция надежности.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Случайная величина X распределена равномерно на отрезке [0; 4]. Найти функцию распределения, математическое ожидание, среднее квадратичное отклонение величины X.

2. Случайная величина X задана функцией распределения вероятностей

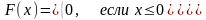
Найти математическое ожидание и дисперсию величины X.

3. Математическое ожидание нормально распределенной случайной величины X равно М(X) = 5, дисперсия равна D (X) = 9. Написать выражение для плотности вероятности.

Модуль 6 Системы случайных величин

Изложены системы случайных величин, ковариация и корреляция, функции случайных величин.

§ 1 Системы случайных величин

Часто результат опыта описывается не одной случайной величиной Х, а несколькими случайными величинами Х₁, Х₂,…, Х_n.

В этом случае говорят, что указанные случайные величины образуют систему (Х₁, Х₂,…, Х_n).

Систему двух случайных величин (X, Y) можно изобразить случайной точкой на плоскости.

Событие, состоящее в попадании случайной точки (X; Y) в область D, обозначим в виде (X; Y) .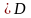

Закон распределения системы двух дискретных случайных величин можно задать в виде табл. 1.

Y X	y1	y2		yn
x1	p11	p12		p1n
x1	p21	p22		p2n
xm	pm1	pm2		pmn

Здесь — вероятность события, заключающегося в одновременном выполнении равенств , т.е. , при этом Таблица может содержать бесконечное множество строк и столбцов.

Законом распределения системы непрерывных случайных величин (X, Y) , будем задавать с помощью плотности вероятности .

Вероятность попадания случайной точки (X; Y) в область D определяется равенством

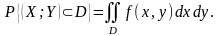
Функция обладает следующими свойствами:

1.

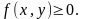
2.

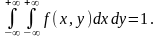
Если все случайные точки (X; Y) принадлежат некоторой конечной области , то условие 1 примет вид

Математические ожидания дискретных случайных величин Х и Y, входящих в систему, определяются так:

(6.1)

а соответствующие характеристики непрерывных случайных величин – по формулам

(6.2)

Точку называют точкой рассеивания системы случайных величин (X, Y).

Дисперсии дискретных случайных величин X и Y определяются формулами

(6.3)

а дисперсии непрерывных случайных величин X, Y определяются формулами

,

(6.4)

.

Средние квадратичные отклонения случайных величин X и Y определяются так:

. (6.5)

Для дисперсии можно использовать также формулу

Пример 6.1. Пусть (X, Y) имеет следующую таблицу распределения:

Y X	-1	0	1
0	0	0,1	0,5
1	0,2	0,1	0,1

Найти математическое ожидание и дисперсии случайных величин X и Y.

Решение. Имеем:

От системы величин (X, Y) перейдем к системе центрированных величин 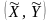, где

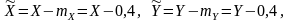
Составим таблицу

	-1,4	-0,4	0,6
-0,4	0	0,1	0,5
0,6	0,2	0,1	0,1

Получаем