Тема 2 Теплопроводность при стационарном режиме
2.1 Передача теплоты через плоскую стенку
При стационарном
тепловом режиме
.
При этом дифференциальное уравнение
теплопроводности
.
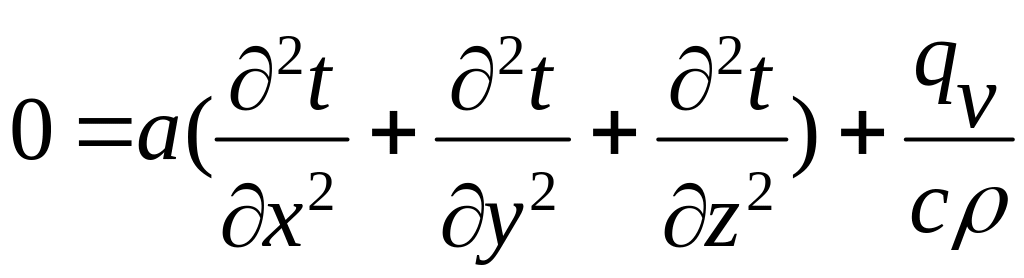Если внутренние источники теплоты отсутствуют (qv=0)
.
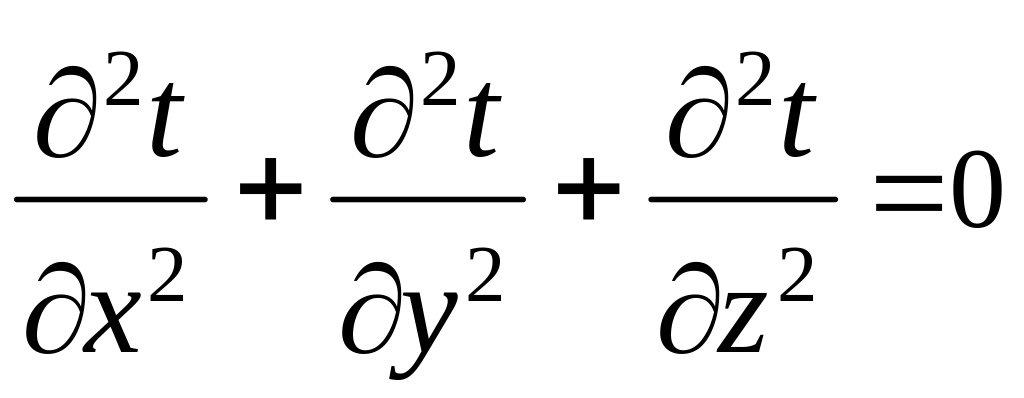Граничные
условия первого рода. Теплопроводность
однослойной плоской стенки. Рассмотрим
однородную и изотропную стенку толщиной
с постоянным коэффициентом теплопроводности
.
На наружных поверхностях стенки
поддерживают постоянными температуры
tс1 и tс2.
П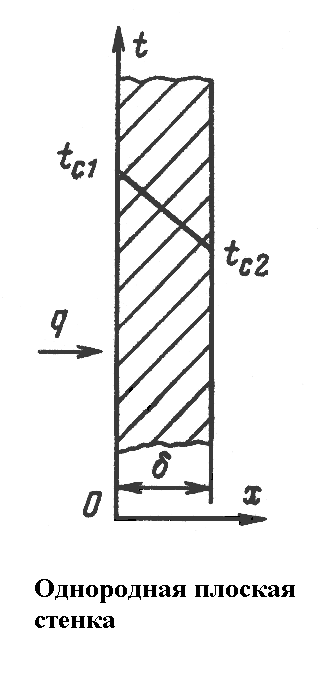
ри
заданных условиях температура будет
изменяться только в направлении,
перпендикулярном плоскости стенки, а
в направлении осей y
и z будет оставаться
постоянной
.
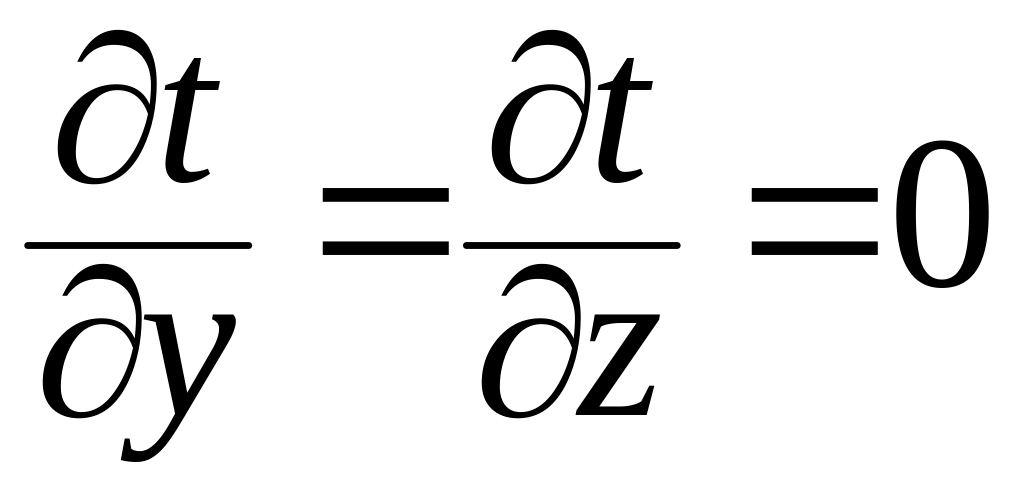В связи с этим дифференциальное уравнение теплопроводности запишется в виде
.
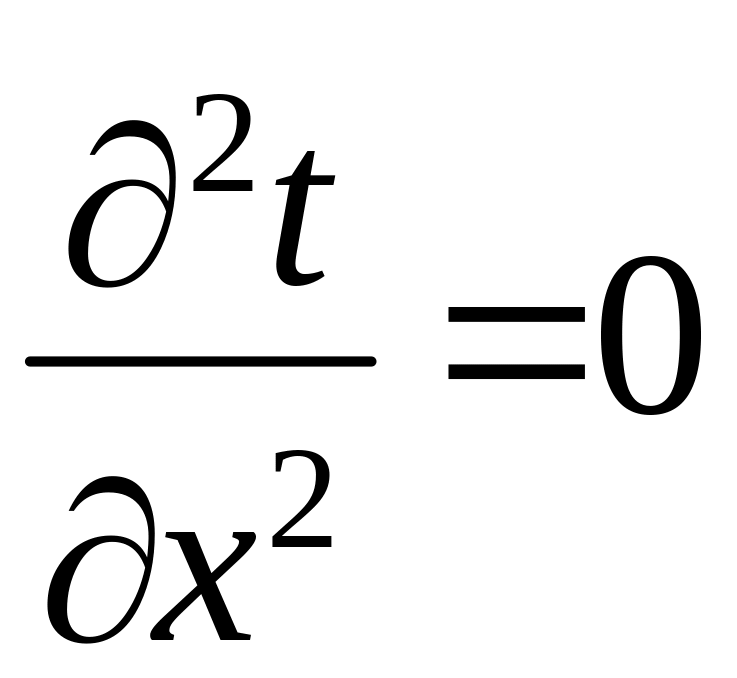Граничные условия задаются следующим образом
х=0, t=tс1,
х= , t=tс2.
Это есть полная математическая формулировка данной задачи, в результате решения которой должны быть найдены распределение температуры в плоской стенке, а также получена формула для определения плотности теплового потока.
Закон распределения температур по толщине стенки найдется в результате двойного интегрирования.
Первое
интегрирование дает
.
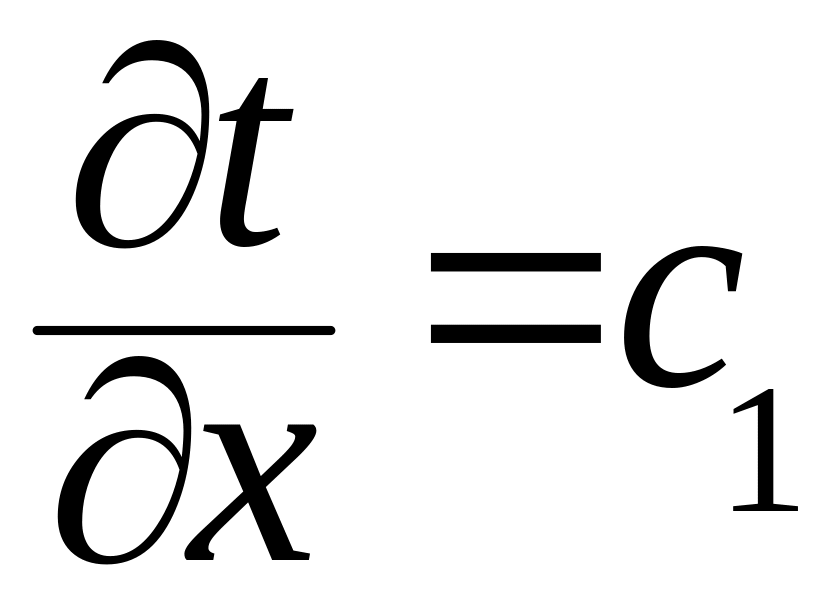После второго интегрирования: t=c1x+c2.
Постоянные с1 и с2 определим из граничных условий.
При
х=0, t=tс1
и с2=tc1;
при х=
,
t=tс2
и c1=-
.
Подставляя значения постоянных с1 и с2 в уравнение получаем закон распределения температуры в плоской стенке
.
Для определения количества теплоты, проходящего через единицу поверхности стенки в единицу времени в направлении оси х, воспользуемся законом Фурье
.
Учитывая,
что
,
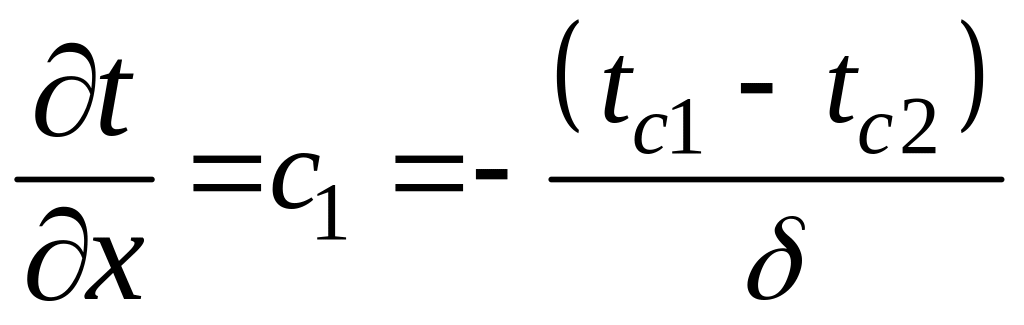после подстановки получаем
.
Количество теплоты,
проходящее через единицу поверхности
стенки в единицу времени, прямо
пропорционально коэффициенту
теплопроводности
,
разности температур на наружных
поверхностях стенки и обратно
пропорционально толщине стенки
.
Тепловой поток определяется не абсолютным
значением температур, а температурным
напором tc1-
tc2=
.
Отношение
,
Вт/(м2К), называется тепловой
проводимостью стенки, а обратная
величина
,
(м2К)/Вт, - термическим сопротивлением
стенки, которое представляет собой
падение температуры в стенке на единицу
плотности теплового потока.
Из уравнения температурного поля получаем
,
откуда следует, что температура в стенке убывает тем быстрее, чем больше плотность потока.
Теплопроводность многослойной плоской стенки. Рассмотрим теплопроводность многослойной стенки, состоящей из n однородных слоев. При стационарном режиме тепловой поток, проходящий через любую изотермическую поверхность неоднородной стенки, будет постоянен
.
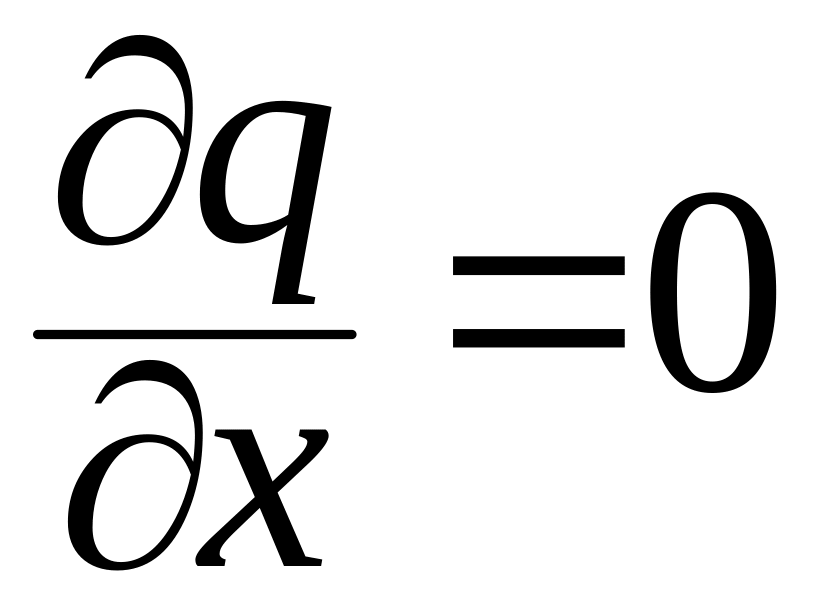При заданных температурах на внешних поверхностях такой стенки, размерах слоев и соответствующих коэффициентах теплопроводности, можно составить систему уравнений
.
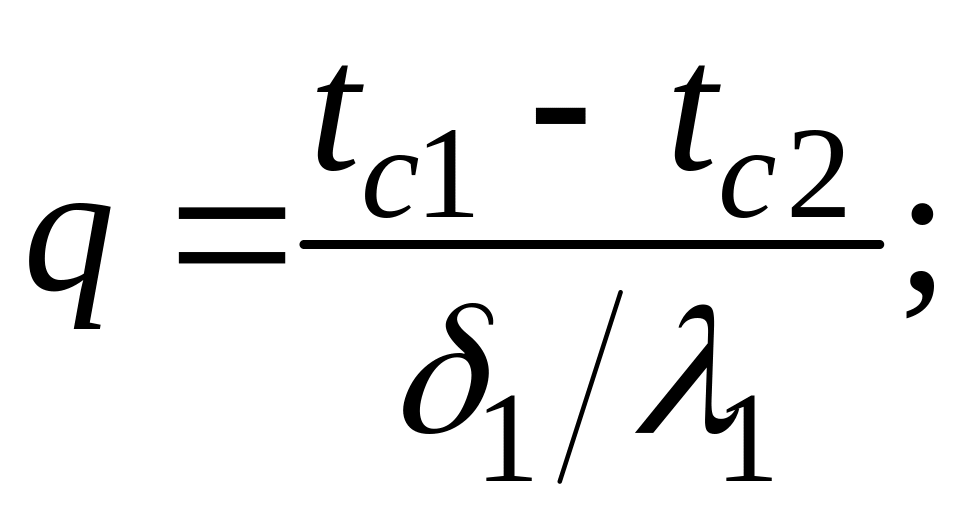
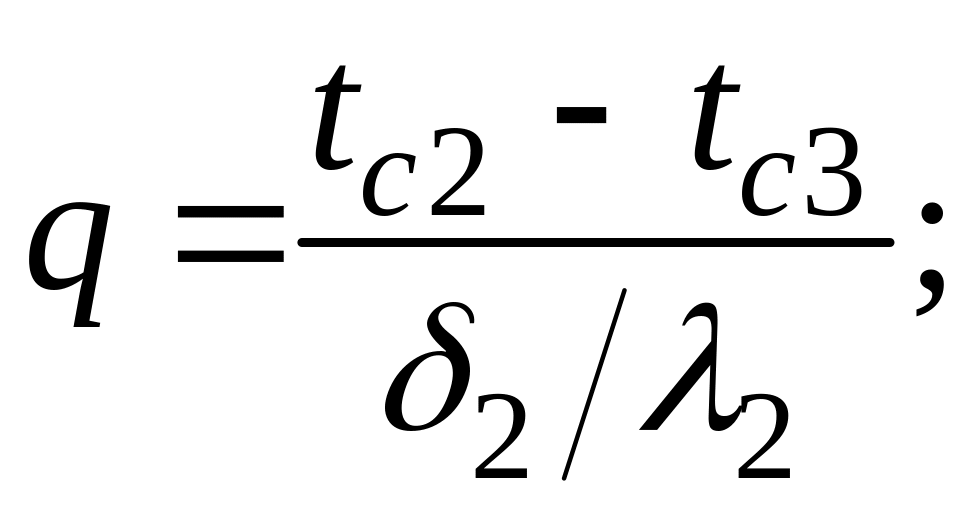
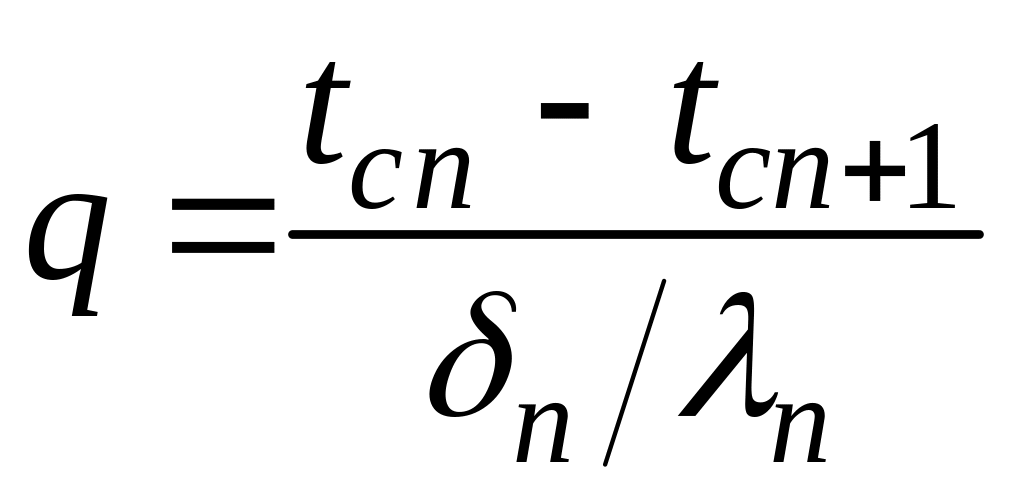Определив температурные напоры в каждом слое и сложив правые и левые части уравнений
.
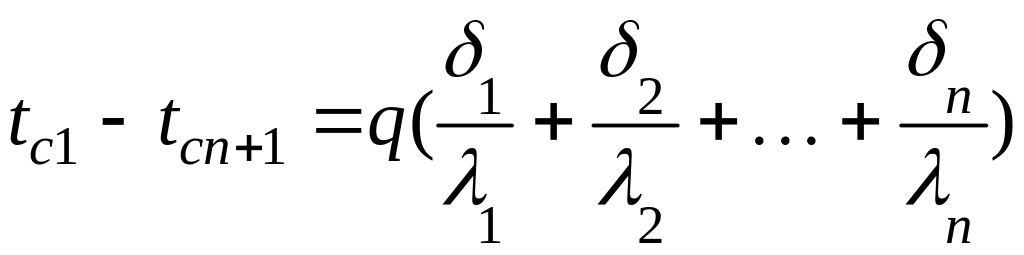Отсюда плотность теплового потока
.
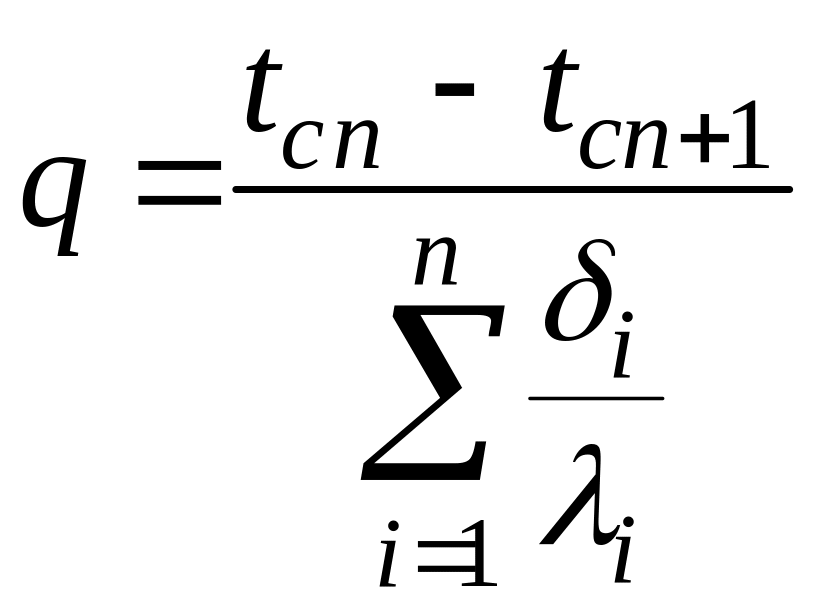Величина
,
равная сумме термических сопротивлений
всех n
слоев,
называется полным
термическим сопротивлением
теплопроводности многослойной стенки.
При сравнении переноса теплоты через многослойную стенку и стенку из однородного материала удобно ввести эквивалентный коэффициент теплопроводности
.
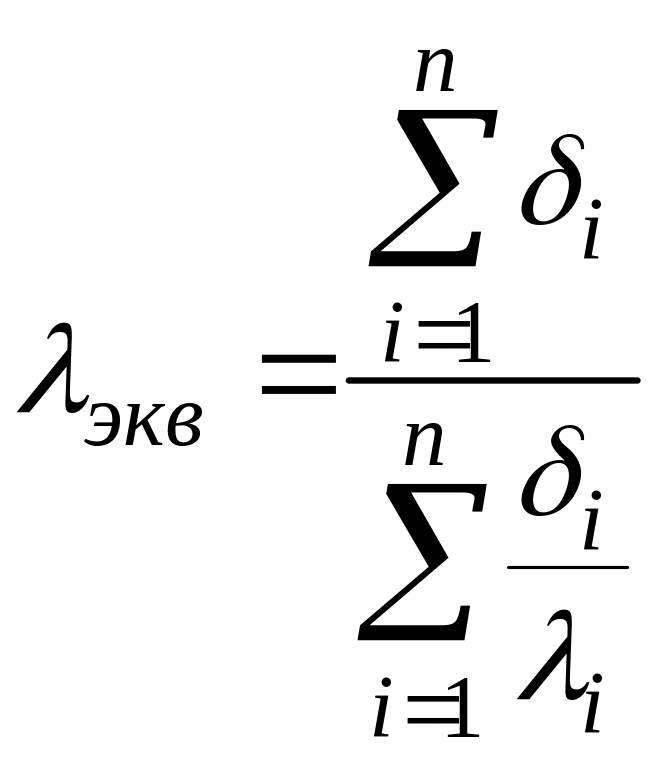Внутри каждого из слоев температура изменяется по линейному закону, а для многослойной стенки в целом температурная кривая представляет ломаную линию.
Граничные условия третьего рода (теплопередача). Передача теплоты из одной среды к другой через разделяющую их стенку однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной среде.
Теплопередача через
плоскую однородную стенку. Пусть
плоская однородная стенка имеет толщину
.
Коэффициент теплопроводности стенки
,
т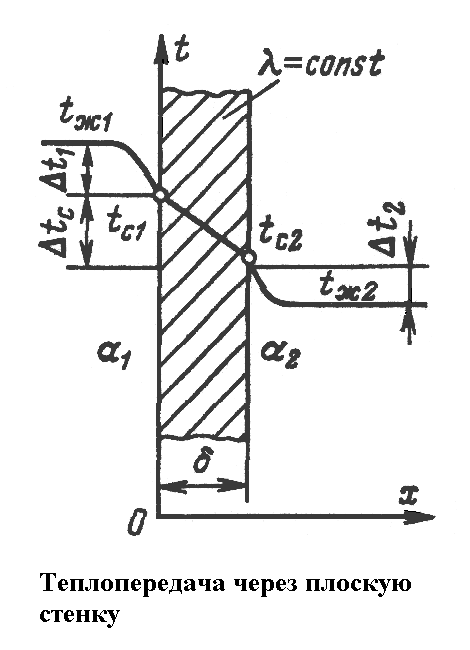
емпературы
окружающей среды tж1
и tж2, а
также коэффициенты теплоотдачи
1
и
2
постоянны. Это позволяет рассматривать
изменение температуры жидкостей и
стенки только в направлении, перпендикулярном
плоскости стенки.
При заданных условиях необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхности стенки.
Согласно уравнению Ньютона-Рихмана плотность теплового потока от горячей жидкости к стенке
.
При стационарном тепловом режиме плотность теплового потока, обусловленная теплопроводностью через твердую стенку
.
Тепловой поток от второй поверхности стенки к холодной жидкости
.
Сложив почленно, и, выразив температурный напор
tж1
- tж2
=
.
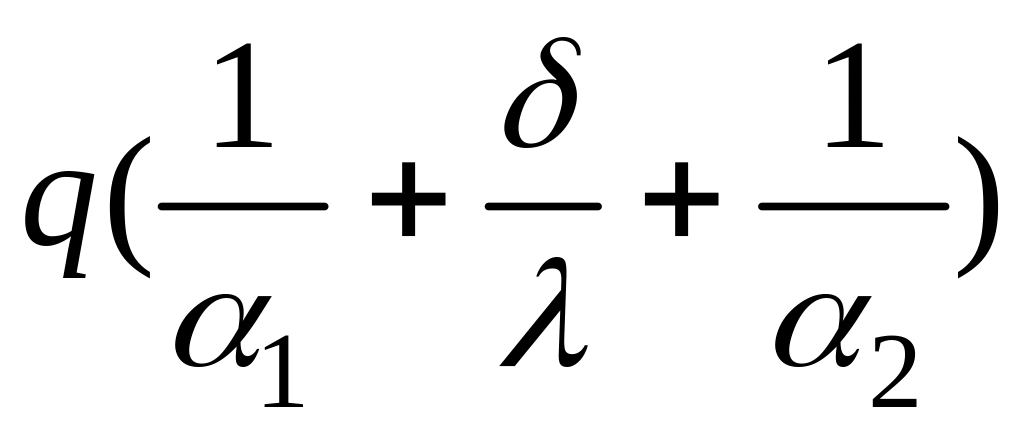Отсюда плотность теплового потока
q=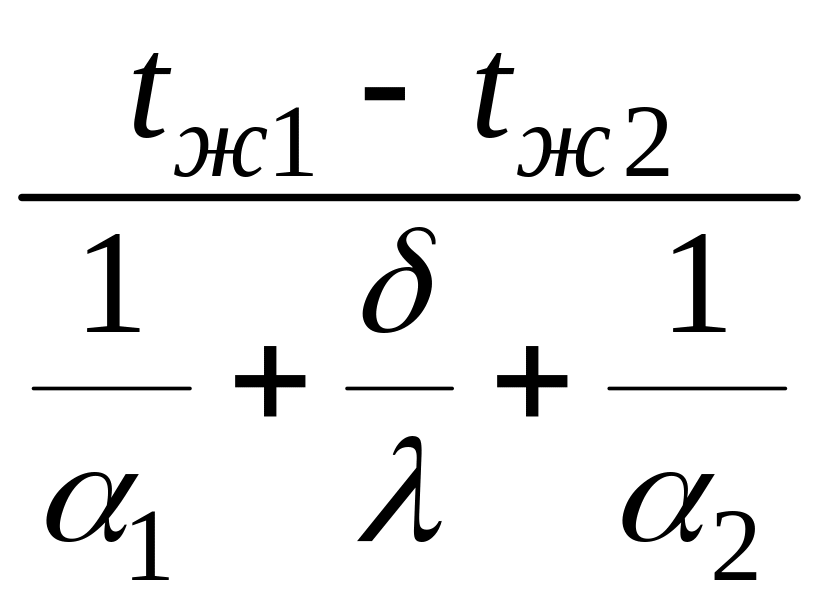
.
Обозначим
.
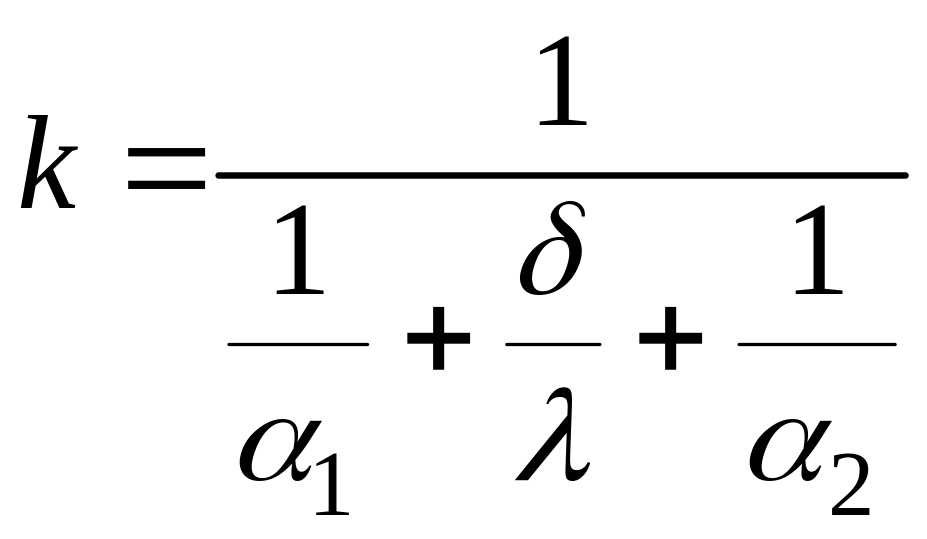Тогда уравнение теплопередачи через плоскую однослойную стенку
.
Величина k называется коэффициентом теплопередачи, Вт/(м2К). Характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку и численно равен количеству теплоты, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус.
Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи
,
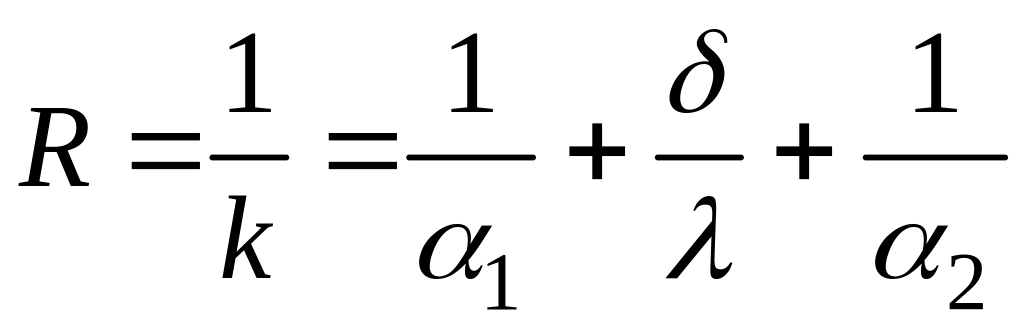где
-
термическое сопротивление теплоотдачи
от горячей жидкости к стенке;
- термическое сопротивление теплопроводности
стенки;
-
термическое сопротивление теплоотдачи
от стенки к холодной жидкости.
Теплопередача через плоскую многослойную стенку. Поскольку общее термическое сопротивление состоит из частных термических сопротивлений, то для многослойной стенки нужно учитывать термическое сопротивление каждого слоя
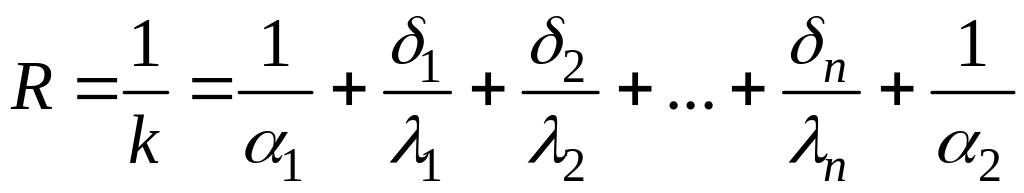или
.
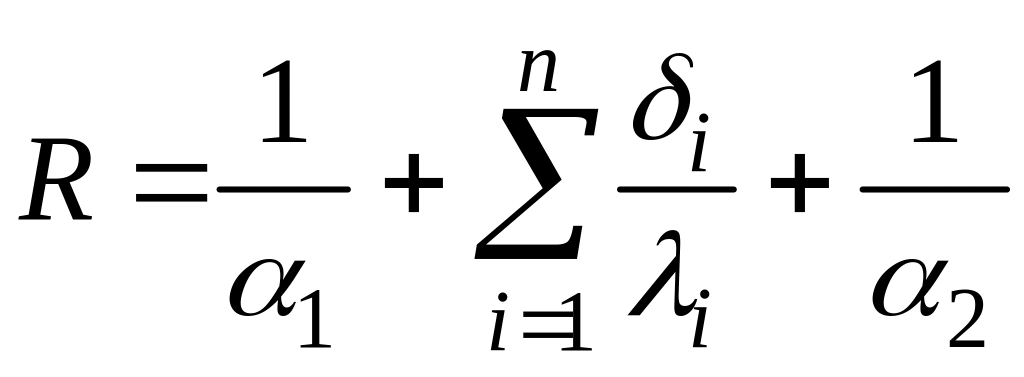Отсюда
.
Плотность теплового потока через многослойную стенку, состоящую из n слоев
q=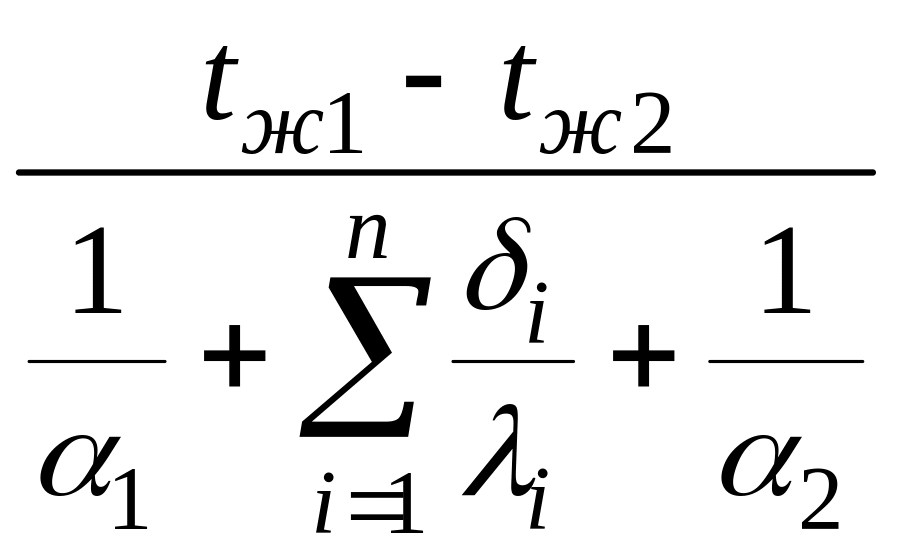
.
Уравнение теплопередачи для многослойной стенки подобно уравнению для однослойной стенки. Различие заключается в выражениях для коэффициентов теплопередачи.
Г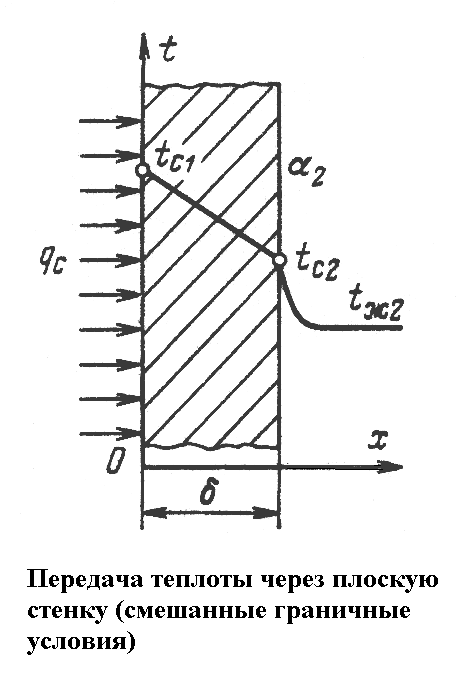
раничные
условия второго и третьего рода. Заданы
граничные условия второго рода на одной
поверхности стенки в виде qc
=
const;
на другой поверхности заданы граничные
условия третьего рода, то есть задан
коэффициент теплоотдачи
и температура жидкости tж2.
Внутренние источники теплоты в стенке
отсутствуют qv=0.
Требуется найти распределение температур
в стенке и температуры на ее поверхности.
Для стационарного теплового процесса
;
.
Из этих уравнений следует, что при заданных значениях qс могут быть определены температуры на поверхностях
tc2
=tж2+
;
tc1
= tж2+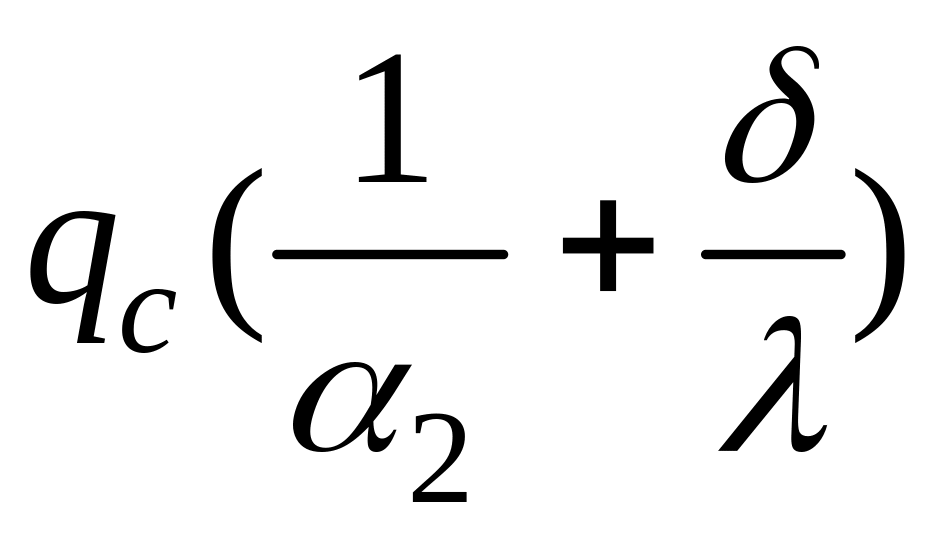
.
Для многослойной стенки: на внешних поверхностях
tc(n+1)
= tж2+
;
tc1
= tж2+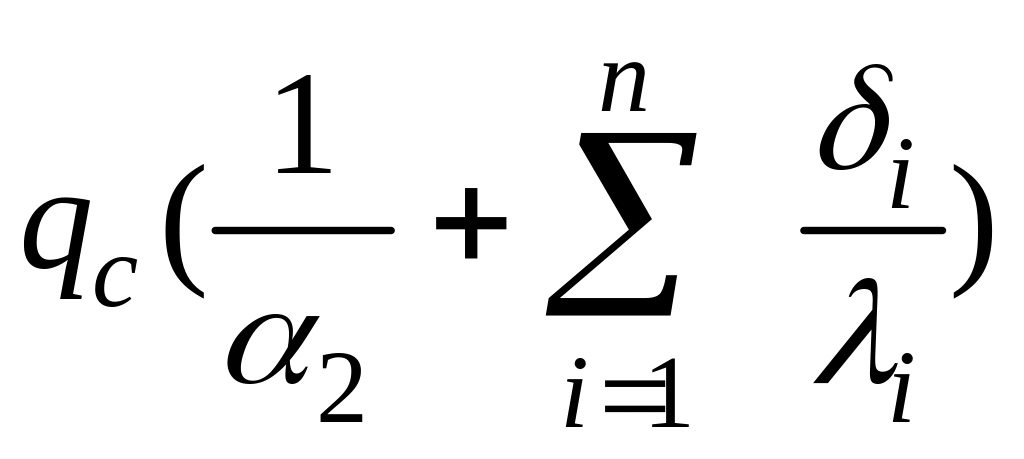
,
на поверхности между слоями
.
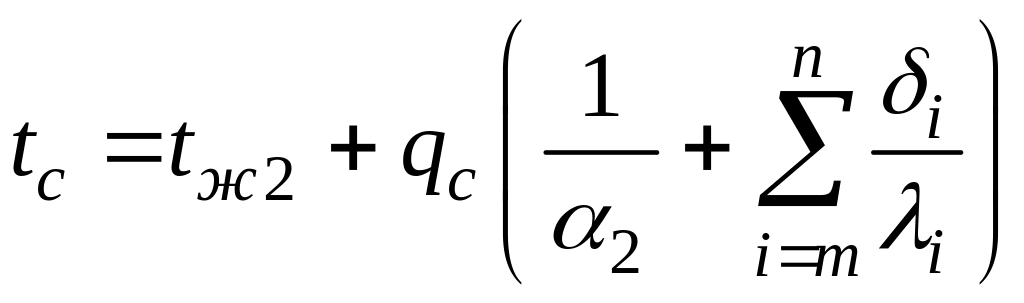