24.Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань

Рис. 5.1

Коливаннями називають процеси, які повторюються з певною періодичністю. В залежності від механізму виникнення коливань розглядають механічні, електромагнітні, електромеханічні і т. п. коливання, а в залежності від характеру сил, що діють на коливну систему, – вільні (власні), згасаючі, вимушені тощо.

Розгляд почнемо з власних механічних коливань горизонтального пружинного маятника, який складається з тіла масою m, закріпленого до кінця пружини, що жорстко прикріплена до стінки (рис. 5.1).

Якщо вивести тіло з положення рівноваги, то на нього почне діяти повертаюча сила пружної деформації пружини, яка задається законом Гука 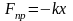. Якщо знехтувати тертям і масою пружини у порівнянні з масою тіла, то при невеликих деформаціях пружини закон руху – ІІ закон Ньютона – запишеться як

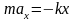, (5.1)

де k – коефіцієнт пружності (жорсткість пружини), х – зміщення тіла від положення рівноваги, а_х – прискорення вздовж осі Х. В подальшому всяку силу, пропорційну до зміщення і напрямлену до положення рівноваги, будемо називати квазіпружною, незалежно від її природи.

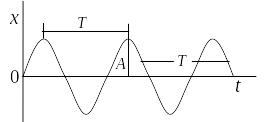Рис. 5.2

Коливання, в яких зміна фізичної величини в залежності від часу відбувається за законом синуса або косинуса, називаються гармонічними. В (5.5): А – амплітуда коливань – найбільше значення коливної фізичної величини (у даному випадку, максимальне зміщення від положення рівноваги), – фаза коливань,  – початкова фаза.

Проміжок часу, протягом якого здійснюється одне повне коливання, називається періодом коливань Т. Зрозуміло, що 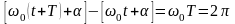, оскільки гармонічні функції повторюються через 2. Звідси циклічна частота

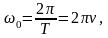(5.6)

де – лінійна частота, як кількість коливань, здійснених за одиницю часу.

Для пружинного маятника , тому період коливань

. (5.7)

Математичний маятник

Математичний маятник – це підвішена на довгій нерозтяжній невагомій нитці матеріальна точка (тіло, розмірами якого нехтують),

Фізичний маятник

Фізичний маятник – це тіло, яке може коливатись навколо осі, що не проходить через його центр мас (рис. 5.4). На рис. 5.4: O – точка підвісу маятника, через яку перпендикулярно до площини рисунка проходить вісь коливання; 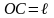– віддаль від осі до центра мас тіла. Повертаючою силою є тангенціальна складова сили тяжіння 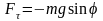, яка при малих кутах відхилення 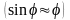є квазіпружною:

Згасання гармонічних коливань

В результаті дії різноманітних сил, які призводять до втрати енергії, коливання можуть згасати. В такому випадку вони описуються формулою

.

Величина називається декрементом згасання коливань. Обернена до декременту величина називається сталою часу згасаючих коливань.

Ангармонічні коливання

Докладніше: Ангармонічні коливання

Періодичні коливання, що не описуються вказаним законом називаються ангармонічними. Якщо величина здійснює коливання із періодом таким чином, що

,

то їхня частота визначається, як .

Ангармонічні коливання, які є періодичною функцією, можна розкласти в ряд Фур'є, тобто записати у вигляді суми гармонічних коливань:

.

Члени цього розкладу називаються гармоніками. В акустиці вищі члени такого розкладу називаються також обертонами; саме вони визначають тембр звуку.

Гармонічні коливання дуже розповсюджені в природі й техніці. До них належать малі коливання підвішеного на пружині тягаря, малі коливання маятника, коливання в молекулах, якими зумовлене поглинання інфрачервоних променів, різноманітні коливання в електротехніці, наприклад у коливальному контурі та інші.