
- •Устойчивость дискретной системы
- •Установившееся значение ошибки дискретной системы
- •Качество управления
- •Частотные характеристики (амплитудно-частотная, логарифмическая)
- •Структурные преобразования
- •Интегрирующее звено (идеальное)
- •Интегрирующее звено с замедлением (реальное интегрирующее звено)
- •Изодромное звено (пи-закон управления)
- •Дифференцирующее звено (идеальное)
- •Дифференцирующее звено с замедлением (реальное дифференцирующее звено)
- •Форсирующее звено 1-го порядка
- •Звено чистого запаздывания
Структурные преобразования
Передаточная функция цепочки последовательно соединенных звеньев = произведению передаточных функций всех звеньев цепочки.
Передаточная функция параллельно соединенных звеньев = сумме передаточных функций всех звеньев, входящих в параллельное соединение.
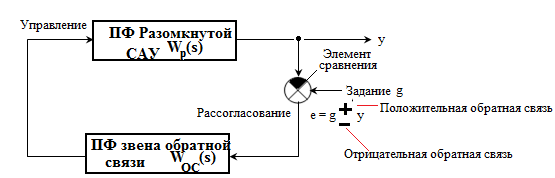
Передаточная
функция звена, охваченного обратной
связью,
равна:
![]() ,
«+»
относится
к ОТРИЦАТЕЛЬНОЙ, а «–»
к ПОЛОЖИТЕЛЬНОЙ обратной связи,
обозначения на рисунке ниже.
,
«+»
относится
к ОТРИЦАТЕЛЬНОЙ, а «–»
к ПОЛОЖИТЕЛЬНОЙ обратной связи,
обозначения на рисунке ниже.
Перенос узла через звено с входа на выход (т.е. по ходу сигнала)
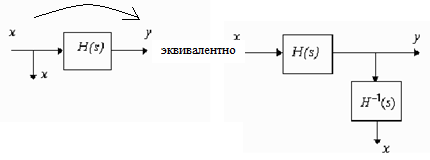
Перенос узла через звено с выхода на вход (т.е. против хода сигнала)
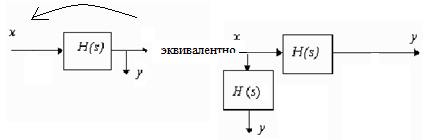
Перенос сумматора через звено с входа на выход (т.е. по ходу сигнала)
Перенос сумматора через звено с выхода на вход (т.е. против хода сигнала)
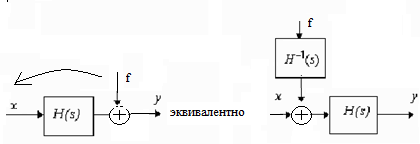
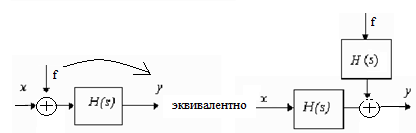
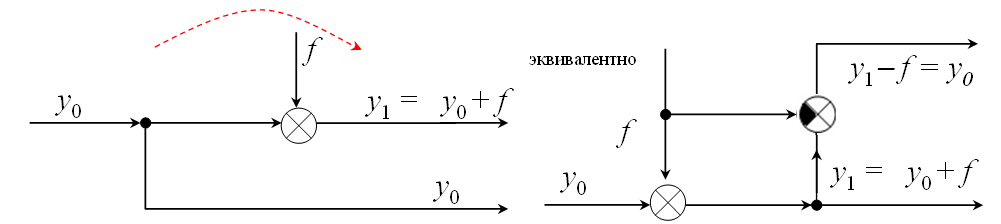
Перенос узла через сумматор по ходу сигнала
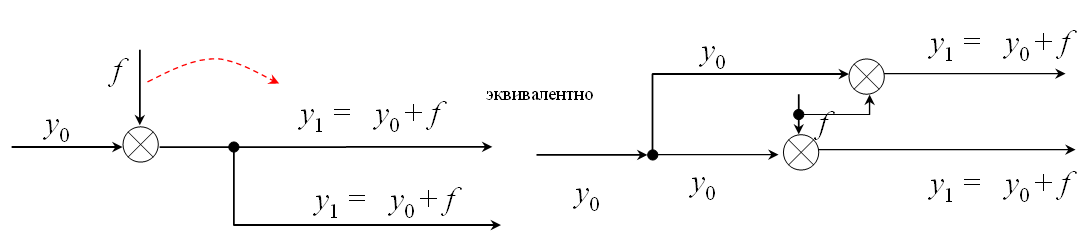
Перенос сумматора через узел по ходу сигнала
Устойчивость
Необходимое (но недостаточное) условие устойчивости: все знаки при элементах знаменателя ПФ ОДИНАКОВЫ.
Пример:
пусть ПФ разомкнутой САУ равна
![]() ,
происходит замыкание
единичной положительной
обратной
связи. Получим:
,
происходит замыкание
единичной положительной
обратной
связи. Получим:
 ’
Слагаемые в знаменателе имеют РАЗНЫЕ
знаки, САУ неустойчива.
’
Слагаемые в знаменателе имеют РАЗНЫЕ
знаки, САУ неустойчива.
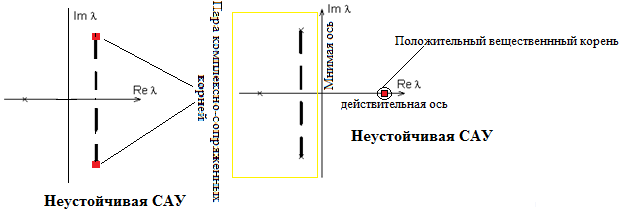
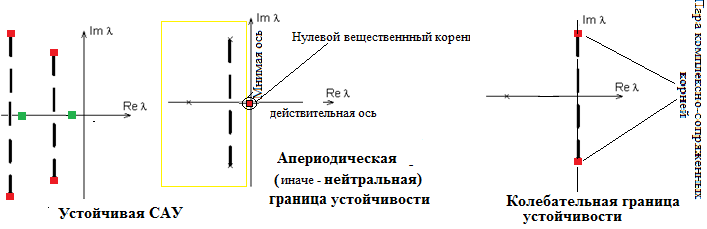
По расположению корней на комплексной плоскости
Правило: в устойчивой САУ все действительные корни уравнения <знаменатель ПФ=0> должны быть отрицательными (на действительной оси комплексной плоскости должны лежать на левой полуоси), все комплексно-сопряженные корни должны иметь отрицательную вещественную часть.
Если хотя бы один действительный корень расположен на правой действительной полуоси или хотя бы одна пара комплексно-сопряженных корней расположена в правой полуплоскости, САУ неустойчива.
Границы устойчивости:
А) Действительный корень равен нулю (находится в начале координат комплексной плоскости) – САУ нейтральна (т.е. выход САУ при снятии входного воздействия не уходит в бесконечность, но и не возвращается к состоянию, которое было до приложения входного воздействия) – апериодическая (иначе – нейтральная) граница устойчивости
Б) Пара комплексно-сопряженных корней является чисто мнимой (действительная часть = 0, корни расположены на мнимой оси) – в САУ возникают незатухающие колебания (т.е. после снятия входного воздействия амплитуда колебаний не уходит в бесконечность, но и не спадает до нуля) – колебательная граница устойчивости
Примеры:
Характерные частоты САУ: (см. также показатели качества по АЧХ, ЛАЧХ)
Частота среза – это значение частоты >0, при которой значение амплитудно-частотной характеристики равно 1 (т.е. A(c) = 1). Можно определить по логарифмической частотной характеристике: ЛАЧХ пересекает ось абсцисс на частоте среза.
Частота, соответствующая полосе пропускания – это значение частоты, соответствующее условию A(п) = 0.707 (на полосе пропускания гасится половина энергии сигнала выхода)
Резонансная частота соответствует пику амплитудно-частотной характеристики.
Элементарные звенья и их характеристики
Динамические свойства звена могут быть определены:
по переходной функции и функции веса
Безынерционное звено (иначе – усилительное звено)
Уравнение
![]() ,
где y(t),
u(t)
– соответственно выход и вход звена, K
–коэффициент усиления.
,
где y(t),
u(t)
– соответственно выход и вход звена, K
–коэффициент усиления.
Передаточная
функция (ПФ)
![]() (здесь
K – коэффициент
усиления)
(здесь
K – коэффициент
усиления)
Частотная ПФ
![]()
Амплитудно-частотная
характеристика (то же самое, что модуль
частотной ПФ) определяется формулой
![]()
Фазовая частотная
характеристика
![]()
Логарифмическая
амплитудная характеристика
:
![]() –
прямая, параллельная абсциссе (наклон
= 0)
–
прямая, параллельная абсциссе (наклон
= 0)
Апериодическое звено 1-го порядка
Уравнение
![]() ,
где y(t),
u(t)
– соответственно выход и вход звена,
K,Т
– соответственно коэффициент усиления
и постоянная времени.
,
где y(t),
u(t)
– соответственно выход и вход звена,
K,Т
– соответственно коэффициент усиления
и постоянная времени.
Передаточная функция (ПФ)
(здесь K – коэффициент усиления, Т – постоянная времени. Свойство: необходимое условие устойчивости одновременно является и достаточным условием.
Частотная ПФ
![]()
Амплитудно-частотная
характеристика (то
же самое, что модуль частотной ПФ)
определяется формулой
![]()
Фазовая частотная
характеристика
![]()
Логарифмическая
амплитудная характеристика
: (асимптотическая) Начальная часть, до
частоты
![]() ,
аппроксимируется прямой, параллельной
абсциссе (значение 20lg(K),
при K=1
равно 0, т.е. совпадает с абсциссой). При
,
аппроксимируется прямой, параллельной
абсциссе (значение 20lg(K),
при K=1
равно 0, т.е. совпадает с абсциссой). При
![]() аппроксимируется
прямой с отрицательным наклоном (– 20
Дб/декаду). Т.е. характерными параметрами
ЛАЧХ при К=0
являются (0;
–20)
аппроксимируется
прямой с отрицательным наклоном (– 20
Дб/декаду). Т.е. характерными параметрами
ЛАЧХ при К=0
являются (0;
–20)
Логарифмическая фазовая характеристика – при изменении частоты изменяется плавно от 0 до (–90), значение (–45) соответствует сопрягающей частоте .
Апериодическое звено 2-го порядка (по сути – последовательное соединение двух апериодических звеньев 1-го порядка с постоянными времени T1, T2 соответственно).
Уравнение
![]() ,
где y(t),
u(t)
– соответственно выход и вход звена,
K,
Т1,Т2
– соответственно коэффициент усиления
и постоянные времени.
,
где y(t),
u(t)
– соответственно выход и вход звена,
K,
Т1,Т2
– соответственно коэффициент усиления
и постоянные времени.
Передаточная функция (ПФ)
Свойство: необходимое условие устойчивости одновременно является и достаточным условием.
Частотная ПФ
![]()
Амплитудно-частотная
характеристика (то же самое, что модуль
частотной ПФ) определяется формулой

Фазовая частотная
характеристика
![]()
Логарифмическая
амплитудная характеристика
: (асимптотическая). Без ограничения
общности примем, что Т1
> T2.
Начальная часть, до частоты
![]() ,
аппроксимируется прямой, параллельной
абсциссе (значение 20lg(K),
при K=1
равно 0, т.е. совпадает с абсциссой). При
,
аппроксимируется прямой, параллельной
абсциссе (значение 20lg(K),
при K=1
равно 0, т.е. совпадает с абсциссой). При
![]() аппроксимируется
прямой с отрицательным наклоном (– 20
Дб/декаду). При
аппроксимируется
прямой с отрицательным наклоном (– 20
Дб/декаду). При
![]() аппроксимируется прямой с отрицательным
наклоном (–40 Дб/декаду). Т.е. характерными
параметрами ЛАЧХ при К=1
являются наклоны (0;
–20; –40),
сопрягающие частоты
аппроксимируется прямой с отрицательным
наклоном (–40 Дб/декаду). Т.е. характерными
параметрами ЛАЧХ при К=1
являются наклоны (0;
–20; –40),
сопрягающие частоты
![]()
Логарифмическая фазовая характеристика – при изменении частоты изменяется плавно от 0 до (–180)
Колебательное звено 2-го порядка.
Уравнение
![]() ,
где y(t),
u(t)
– соответственно выход и вход звена,
K,
Т,
– соответственно коэффициент усиления,
постоянная времени и коэффициент
затухания.
,
где y(t),
u(t)
– соответственно выход и вход звена,
K,
Т,
– соответственно коэффициент усиления,
постоянная времени и коэффициент
затухания.
Передаточная функция (ПФ)
Свойство: необходимое условие устойчивости одновременно является и достаточным условием.
Частотная ПФ
![]()
Амплитудно-частотная
характеристика (то
же самое, что модуль частотной ПФ)
определяется формулой
![]()
Фазовая частотная
характеристика
![]()
Логарифмическая
амплитудная характеристика : При
![]() –
параллельна
оси абсцисс, равна 20lg(K).
Имеет резонансный пик при
–
параллельна
оси абсцисс, равна 20lg(K).
Имеет резонансный пик при
![]() .
При
.
При
![]() аппроксимируется
прямой с отрицательным наклоном (– 40
Дб/декаду). Характерные параметры при
K =1: наклоны (0; – 40), изменение наклона
на сопрягающей частоте
аппроксимируется
прямой с отрицательным наклоном (– 40
Дб/декаду). Характерные параметры при
K =1: наклоны (0; – 40), изменение наклона
на сопрягающей частоте
Логарифмическая фазовая характеристика – при изменении частоты изменяется плавно от 0 до (–180)
Консервативное звено.
Уравнение
![]() ,
где y(t), u(t) – соответственно выход и вход
звена, K, Т – соответственно коэффициент
усиления и постоянная времени.
,
где y(t), u(t) – соответственно выход и вход
звена, K, Т – соответственно коэффициент
усиления и постоянная времени.
Передаточная функция (ПФ)
Свойство: звено находится на границе устойчивости колебательного типа (незатухающие колебания с постоянной амплитудой).
Частотная ПФ
![]()
Амплитудно-частотная
характеристика (то же самое, что модуль
частотной ПФ) определяется формулой
![]() ; имеет
разрыв на резонансной частоте
; имеет
разрыв на резонансной частоте
![]() .
.
Фазовая частотная
характеристика
![]() (ступенчатое
изменение при
)
(ступенчатое
изменение при
)
Логарифмическая
амплитудная характеристика :
Имеет разрыв при
.
При
![]() аппроксимируется
прямой с отрицательным наклоном (– 40
Дб/декаду).
аппроксимируется
прямой с отрицательным наклоном (– 40
Дб/декаду).
Логарифмическая
фазовая характеристика
![]()
(ступенчатое изменение при )
