Частотные характеристики (амплитудно-частотная, логарифмическая)

Построение: Шаг 1. Получить частотную передаточную функцию по обычной передаточной функции. Частотная передаточная функция строится по передаточной функции H(s) путем замены оператора s на комплексный аргумент (j) (здесь – мнимая единица,  ­– частота). Пример: пусть передаточная функция САУ равна В. Заменяем: . Получим частотную передаточную функцию . Шаг 2. Получить действительную и мнимую частотные характеристики (ЧХ). Разделяем W(j) на сумму действительной и мнимой части. Если в знаменателе есть комплексное слагаемое – нужно умножить и числитель, и знаменатель на выражение, комплексно-сопряженное к знаменателю. В примере знаменатель не содержит комплексного слагаемого. Получим: , здесь Re(…) Im(…) – соответственно действительная и мнимая ЧХ. Шаг 3. Получить амплитудно-частотную и фазовую частотную ЧХ. Для этого используется формула Эйлера, позволяющая получить: вместо эквивалентное выражение . Здесь - амплитудно-частотная характеристика. В примере . - фазовая частотная характеристика. В примере .

Амплитудно-частотная характеристика (АЧХ) – это зависимость амплитуды выхода САУ от частоты  единичного синусоидального сигнала, поступающего на вход. Для построения АЧХ необходимо найти модуль частотной передаточной функции (для чего нужно разделить частотную ПФ на действительную и мнимую части и найти зависимость корня квадратного от суммы квадратов этих частей от частоты). Пример: Если , то вычисляем: . АФХ равна:

Фазовая частотная характеристика (ФЧХ) – это зависимость сдвига фазы выхода САУ по отношению к входу САУ от частоты  единичного синусоидального сигнала, поступающего на вход. Для построения ФЧХ необходимо разделить частотную ПФ на действительную и мнимую части и вычислить арктангенс отношения мнимой части к действительной. Пример: Если , то вычисляем: . ФЧХ равна:

Логарифмическая амплитудно-частотная характеристика (ЛАЧХ). Определение: ЛАЧХ – это зависимость десятичного логарифма амплитудно-частотной характеристики A() от частоты  (измеряется в децибелах, Дб, шкала ординаты 20Дб). Из соображений масштаба формулу записывают так: . Ось абсцисс – в логарифмическом масштабе, поэтому ось ординат нельзя провести для  = 0 (нуль не имеет логарифма). Эту ось проводят произвольно. ЛАХ принято аппроксимировать отрезками прямых линий.

Построение ЛАЧХ. Используется аппроксимация ЛАЧХ асимптотическими прямыми линиями. Пример: пусть разомкнутая САУ состоит из последовательного соединения звеньев:

Расположение звеньев – в порядке убывания постоянных времени (только для удобства объяснения; порядок звеньев в последовательной цепи безразличен). Пусть

Поскольку амплитудно-частотная характеристика (АЧХ) последовательно соединенных звеньев = произведению АЧХ каждого звена, логарифмическая АЧХ (ЛАЧХ) будет равна сумме ЛАЧХ каждого звена. Асимптотические ЛАЧХ всех звеньев описаны в разделе «Звенья САУ». Строим асимптотические ЛАЧХ каждого звена и суммируем. Масштаб по оси абсцисс – логарифмический, по оси ординат 0 обычный.

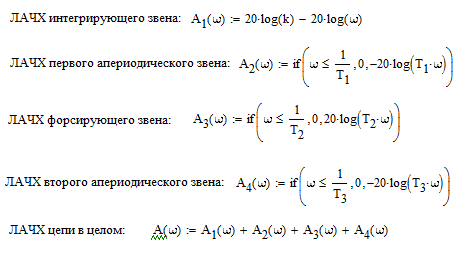
ЛАЧХ цепи в целом представляет собой отрезки, соединяющиеся по сопрягающим частотам: . Общая идея: пока частота меньше сопрягающей, значением частоты можно пренебречь; если частота больше сопрягающей, то можно пренебречь единицей по сравнению со слагаемым, содержащим частоту в качестве сомножителей.

Характерные элементы ЛАЧХ (см. также логарифмические характеристики элементарных звеньев):

1. Пересекает ось ординат в точке 20lg(K), где K – коэффициент усиления САУ (его можно найти по передаточной функции, полагая в частотной передаточной функции частоту =0 или в обычной ПР полагая s = 0).

2. Апериодическое звено 1-го порядка (ПФ , где K,T – соответственно коэффициент усиления и постоянная времени) имеет асимптотическую ЛАЧХ с наклонами (0 и –20 Дб/декаду)

3. Интегрирующее звено (ПФ ) имеет ЛАЧХ в виде нисходящей прямой линии с наклоном (– 20 Дб/декаду)

4. Дифференцирующее звено (ПФ ) имеет ЛАЧХ в виде восходящей прямой линии с наклоном (+ 20 Дб/декаду)

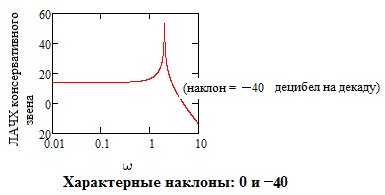
5. Консервативное звено (ПФ ) имеет ЛАЧХ с разрывом на частоте =1/T. Характерные наклоны: 0 до частоты разрыва и (–40 Дб/декаду) после частоты разрыва: