1.4. Тригонометрична форма комплексного числа. Дії над комплексними числами, заданими у тригонометричній формі

Нехай – модуль, а – одне із значень аргументу комплексного числа . Оскільки із співвідношення (1.6) випливає, що , то

(1.8)

Таким чином, будь-яке комплексне число можна записати за формулою (1.8), де r – модуль, а – одне із значень аргументу цього числа.

Справедливе і обернене твердження: якщо комплексне число представлене у вигляді (1.8), де , то .

Представлення комплексного числа у вигляді

де , називається тригонометричною формою запису комплексного числа.

Алгоритм представлення комплексного числа в тригонометричній формі: знайти модуль цього числа та обчислити одне із значень аргументу цього числа.

Зауваження. В силу багатозначності тригонометрична форма комплексного числа також неоднозначна.

Добуток комплексних чисел і знаходиться за формулою

(1.9)

тобто

Правило множення комплексних чисел, заданих в тригонометричній формі: при множенні двох комплексних чисел, заданих у тригонометричній формі, їх модулі перемножуються, а аргументи додаються.

Частка комплексних чисел і , причому , знаходиться за формулою

, (1.10)

тобто

.

Правило ділення комплексних чисел, заданих в тригонометричній формі: при діленні комплексних чисел, заданих у тригонометричній формі, їх модулі діляться, а аргументи віднімаються.

Для піднесення комплексного числа до n-го ступеня використовується формула

(1.11)

яка називається формулою Муавра.

Для добування кореня n-го ступеня із комплексного числа використовується формула

(1.12)

де – арифметичній корінь n-го ступеня, .

Приклади. 1.11. Представити в тригонометричній формі наступні числа: 1) 2; 2) 6і; 3) ; 4)  ; 5) .

 1) і так як вектор, який відображає число 2, лежить на додатній піввісі Ox, то головне значення аргументу , тобто або ;

2) і оскільки вектор, який відображає число 6і, лежить на додатній піввісі Oy, головне значення аргументу ; тому або

;

3) , тому точка, яка відображає число z, лежить у ІІ чверті, тобто , , значить, або

;

4) , тому точка, яка відображає число z, лежить у ІV чверті; , значить, або ;

5) , тому точка, яка відображає число z, лежить у ІІІ чверті; , тоді або 

1.12. Представити в алгебраїчній формі числа:

1) ; 2) .

 1) Підставивши значення в дане рівняння, отримаємо ;

2) маємо . 

1.13. Знайти добуток: .

 За формулою (1.9) одержимо



1.14. Виконати ділення: .

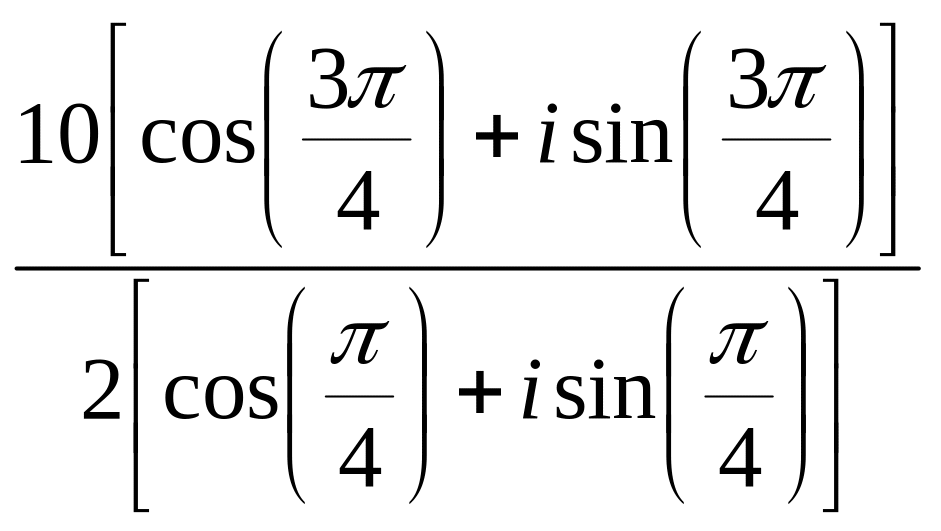 За формулою (1.10) одержимо



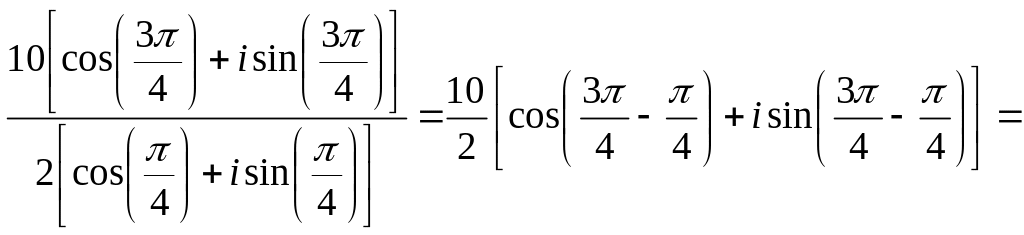
1.15. Піднести до ступеня: 1) ; 2) .

 1) За формулою Муавра одержимо

;

2) подамо число в тригонометричній формі, оскільки , то , значить, точка, яка відображає дане число, лежить в IV чверті, тому 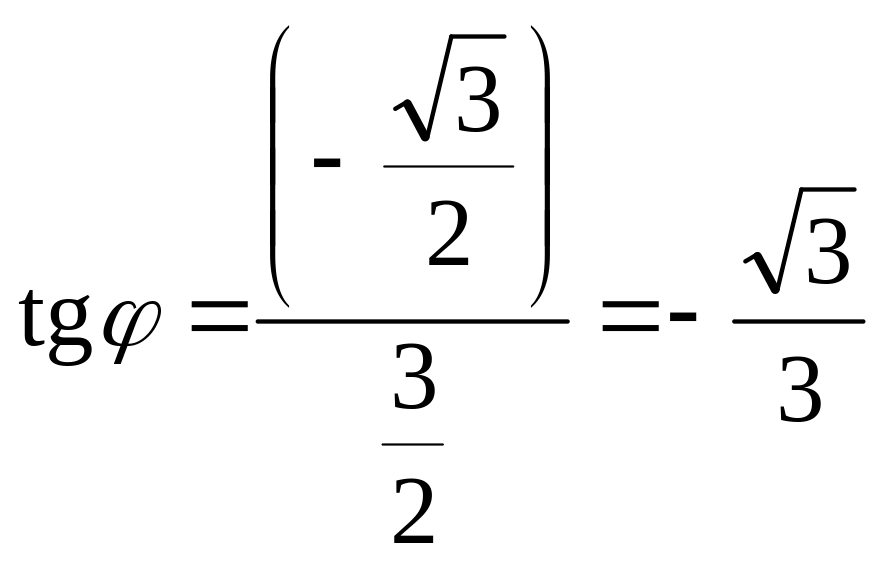, тобто , отже, Значить,



1.16. Використовуючи формулу Муавра, довести справедливість наступних тотожностей:

 Поклавши у відношенні (1.11) і , одержимо

або

Із умови рівняння двох комплексних чисел випливає, що

Аналогічно, покладаючи в співвідношенні (1.11) і , маємо

тобто

Із умови рівності двох комплексних чисел випливає:



1.17. Добути корені із комплексних чисел: 1) ; 2) .

 1) Подамо число і у тригонометричній формі: . За формулою (1.12) одержимо ,

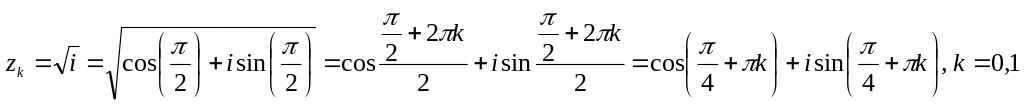якщо , то ,

якщо , то ;

2) Представимо число 1 у тригонометричній формі: . За формулою (1.12) знайдемо

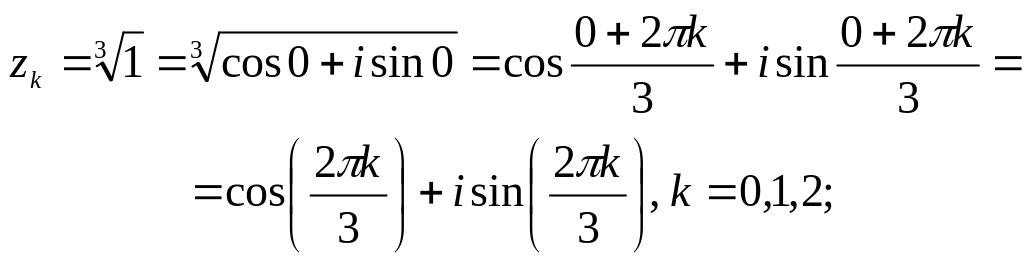
якщо , то ,

якщо , то ,

якщо , то . 