
- •Тема 1. Комплексні числа та дії над ними
- •1.1. Введення поняття комплексного числа
- •1.2. Алгебраїчна форма запису комплексних чисел та дії над комплексними числами, записаними у цій формі
- •Властивості спряжених чисел
- •1.3. Геометричне зображення комплексного числа. Модуль та аргумент комплексного числа
- •1.4. Тригонометрична форма комплексного числа. Дії над комплексними числами, заданими у тригонометричній формі
- •1.5. Показникова функція з комплексним показником. Формули Ейлера. Показникова форма комплексного числа
- •Додаток 1 Комплексні числа та дії над ними
Лінійна і векторна алгебра та аналітична геометрія
Тема 1. Комплексні числа та дії над ними
1.1. Введення поняття комплексного числа
При розв’язанні квадратних
алгебраїчних рівнянь виникла проблема
тоді, коли дискримінант
![]() виявлявся числом від’ємним, і стало
зрозуміло, що дуже корисно і зручно не
ігнорувати символ
виявлявся числом від’ємним, і стало
зрозуміло, що дуже корисно і зручно не
ігнорувати символ
![]() і вирази
і вирази
![]() (де
(де
![]() ),
а оперувати з ними (чисто формально!),
як із звичайними числами. А саме, якщо
позначити
),
а оперувати з ними (чисто формально!),
як із звичайними числами. А саме, якщо
позначити
![]() та оперувати з виразами
та оперувати з виразами
![]() за звичайними правилами
за звичайними правилами
![]() (1.1)
(1.1)
то при цьому виконуються всі
звичайні властивості додавання та
множення. Отже, з цієї точки зору вирази
мають таке саме право називатися числами,
як вираз
![]() (де
(де
![]() )
– раціональними чис
)
– раціональними чис
лами, або нескінченні десяткові дроби – дійсними числами.
Якщо вважати, що
![]() – це просто дійсне число а,
що і –
це
– це просто дійсне число а,
що і –
це
![]() ,
то у відповідності з (5.1)
,
то у відповідності з (5.1)
![]() і, отже, вираз
утворюється з
та
і, отже, вираз
утворюється з
та
![]() шляхом заданого в (1.1) алгоритму множення
та додавання, тобто
шляхом заданого в (1.1) алгоритму множення
та додавання, тобто
![]() .
.
Отже, будь-яке квадратне
рівняння виду
![]() ,
де р і
q –
дійсні числа, має два корені, тобто:
,
де р і
q –
дійсні числа, має два корені, тобто:
якщо дискримінант
 ,
то дане рівняння має два різних дійсних
кореня
,
то дане рівняння має два різних дійсних
кореня
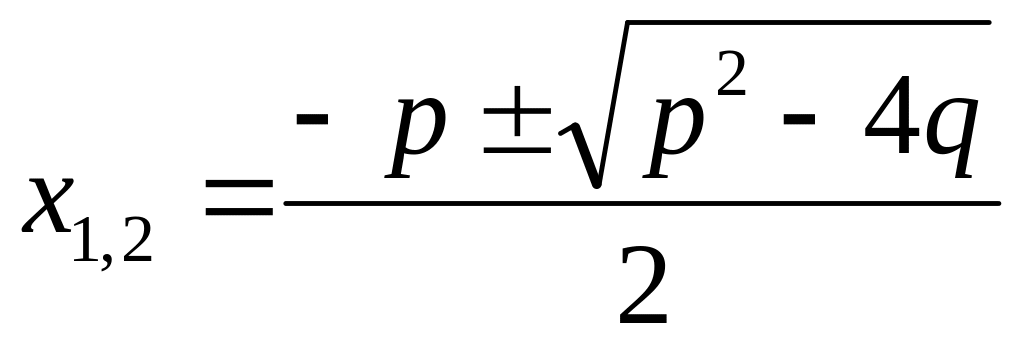 ;
;якщо дискримінант
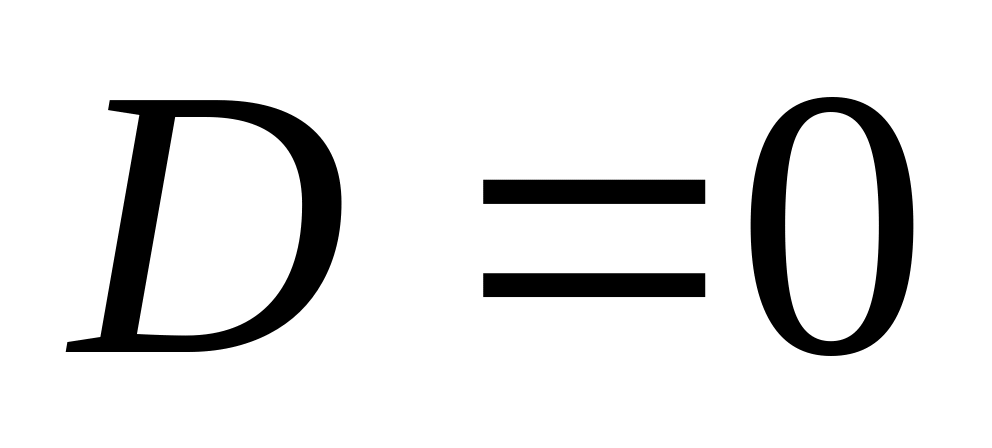 ,
то дане рівняння має два рівних дійсних
кореня
,
то дане рівняння має два рівних дійсних
кореня
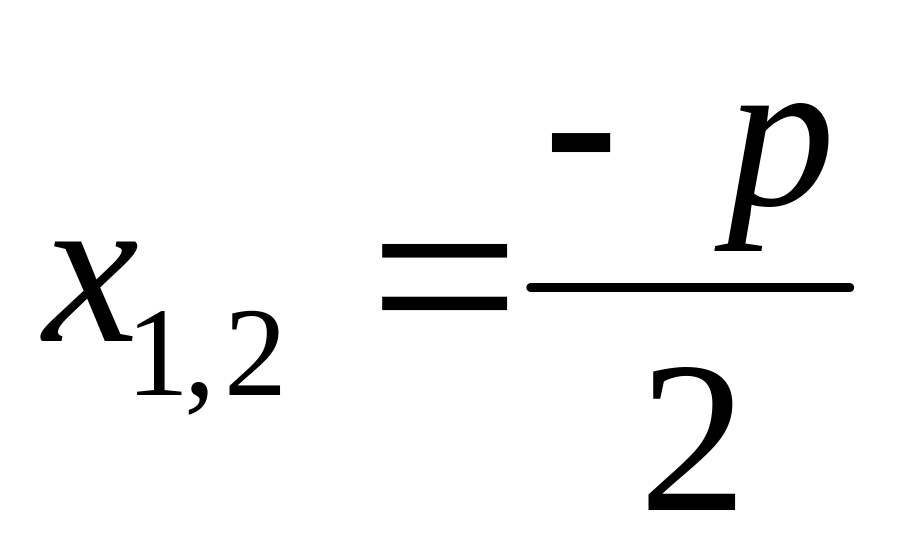 ;
;якщо дискримінант
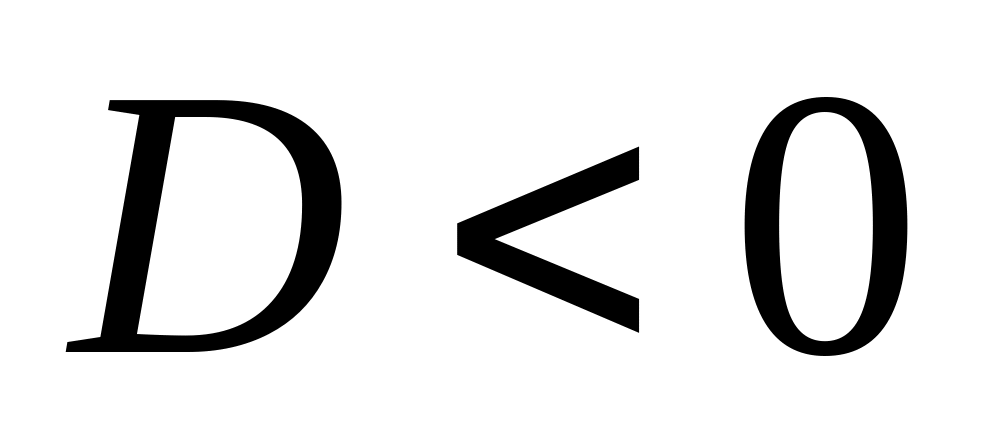 ,
то дане рівняння має два різних
комплексних кореня
,
то дане рівняння має два різних
комплексних кореня
![]() .
.
Приклади.
1.1.
Розв’язати рівняння
![]() .
.
Знаходимо
дискримінант
![]() .
.
За останньою формулою маємо
![]() ,
або
,
або
![]() та
та
![]() .
.
1.2.
Розв’язати рівняння
![]() .
.
Знаходимо
дискримінант
![]() ,
отже
,
отже
![]() .
.
Твердження відоме під назвою „основна теорема алгебри”, доведення якої було дане Гаусом в кінці XVIII ст., має місце для алгебраїчних рівнянь будь-якого ступеня з довільними комплексними коефіцієнтами.
Таким чином, ми отримуємо
своєрідне розширення множини дійсних
чисел, породжене приєднанням до R
уявного елементу
,
тобто такого, що
![]() .
.
1.2. Алгебраїчна форма запису комплексних чисел та дії над комплексними числами, записаними у цій формі
Комплексними числами
називаються вирази
виду
,
де а і
b –
дійсні числа, а число і,
що визначається рівністю
,
називається уявною
одиницею, причому дійсне
число а
називається дійсною
частиною комплексного
числа
![]() і позначається
і позначається
![]() ,
число
,
число
![]() – уявною
частиною і
позначається
– уявною
частиною і
позначається
![]() ,
а дійсне число b
– коефіцієнтом
уявної
частини.
Множина комплексних чисел позначається
С (від
Complex).
,
а дійсне число b
– коефіцієнтом
уявної
частини.
Множина комплексних чисел позначається
С (від
Complex).
Два комплексні числа
![]() і
і
![]() називаються рівними,
якщо їхні дійсні та уявні частини
відповідно рівні, тобто коли
називаються рівними,
якщо їхні дійсні та уявні частини
відповідно рівні, тобто коли
![]() і
і
![]() .
.
Сумою
двох комплексних чисел
і
називається комплексне
число, дійсна
частина якого дорівнює сумі дійсних
частин доданків, а коефіцієнт уявної
частини – відповідно сумі коефіцієнтів
уявної частини доданків, тобто![]() .
.
Добутком
двох комплексних чисел
і
називається комплексне
число, дійсна
частина якого дорівнює
![]() ,
а уявна –
,
а уявна –
![]() .
.
Запис комплексного числа у вигляді називається алгебраїчною формою комплексного числа.
Будь-яке дійсне число а
міститься в множині комплексних чисел,
тому що його можна записати так:
![]() .
Числа 0, 1 та і
записуються відповідно у вигляді
.
Числа 0, 1 та і
записуються відповідно у вигляді
![]() ,
,
![]() і
і
![]() .
При
.
При
![]() комплексне число
перетворюється в чисто уявне число
.
комплексне число
перетворюється в чисто уявне число
.
Комплексні числа вигляду
і
![]() називаються протилежними.
називаються протилежними.
Комплексне число
![]() називається спряженим
з числом
і позначається
називається спряженим
з числом
і позначається
![]() ,
тобто
,
тобто
![]() ,
але до числа
також можна знайти спряжене число, яким
буде число
,
але до числа
також можна знайти спряжене число, яким
буде число
![]() ,
тому можна вести мову про пару спряжених
чисел. Наприклад, до числа
,
тому можна вести мову про пару спряжених
чисел. Наприклад, до числа
![]() протилежним є число
протилежним є число
![]() ,
а спряженим
,
а спряженим
![]() .
.
