
- •Тема 1. Комплексні числа та дії над ними
- •1.1. Введення поняття комплексного числа
- •1.2. Алгебраїчна форма запису комплексних чисел та дії над комплексними числами, записаними у цій формі
- •Властивості спряжених чисел
- •1.3. Геометричне зображення комплексного числа. Модуль та аргумент комплексного числа
- •1.4. Тригонометрична форма комплексного числа. Дії над комплексними числами, заданими у тригонометричній формі
- •1.5. Показникова функція з комплексним показником. Формули Ейлера. Показникова форма комплексного числа
- •Додаток 1 Комплексні числа та дії над ними
Властивості спряжених чисел
1. Сума і
добуток спряжених комплексних чисел є
числа дійсні, так як
![]() і
і
![]() .
.
2. Число,
спряжене з сумою двох чисел, дорівнює
сумі чисел, спряжених з доданками, тобто
![]() .
.
3. Число,
спряжене з добутком двох чисел, дорівнює
добутку чисел, спряжених з співмножниками,
тобто
![]() .
.
4. Число,
спряжене з різницею двох чисел, дорівнює
різниці чисел, спряжених зі зменшуваним
![]() і від’ємником
і від’ємником
![]() ,
тобто
,
тобто
![]() .
.
5. Число,
спряжене з часткою двох чисел, дорівнює
частці чисел, спряжених з діленим
і дільником
,
тобто
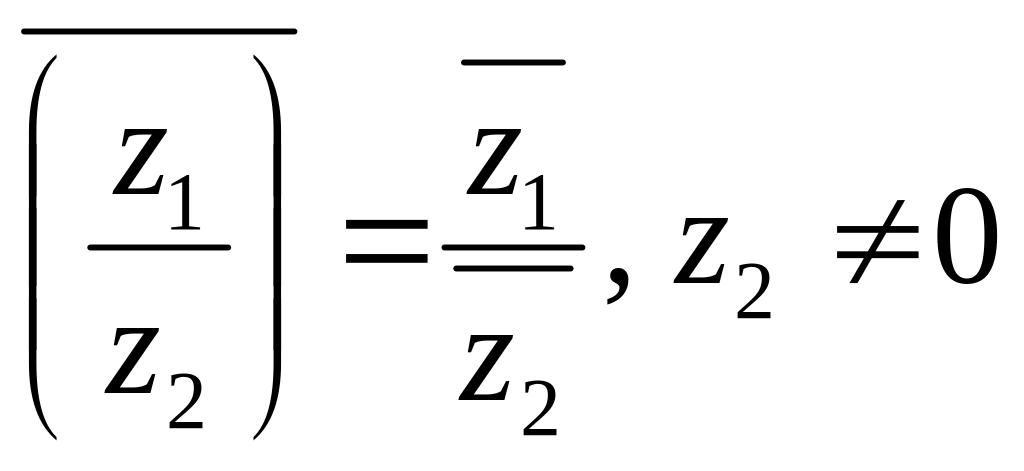 .
.
Розглядаючи віднімання і ділення комплексних чисел як дії, обернені відповідно додаванню і множенню, одержимо правила віднімання і ділення комплексних чисел.
Правило віднімання комплексних
чисел: для
того, щоб відняти два комплексних числа
![]() та
та
![]() ,
потрібно окремо знайти різниці дійсної
та уявної частин і результати відповідно
записати, тобто
,
потрібно окремо знайти різниці дійсної
та уявної частин і результати відповідно
записати, тобто
![]() (1.2)
(1.2)
Правило ділення комплексних
чисел: для того, щоб
поділити два комплексних числа
та
,
потрібно і чисельник і знаменник
отриманого дробу
![]() помножити на число, спряжене до знаменника,
тобто числа
;
отже,
помножити на число, спряжене до знаменника,
тобто числа
;
отже,
 .
(1.3)
.
(1.3)
Приклади.
1.3.
Виконати дії:![]() .
.
За правилом додавання комплексних чисел маємо
![]()
1.4.
Виконати дії:![]() .
.
За правилом віднімання комплексних чисел одержимо
![]()
1.5.
Виконати
дії:![]() .
.
Згідно з правилом множення комплексних чисел
![]()
1.6.
Виконати
дії:![]() .
.
![]()
1.7.
Знайти
дійсні числа х
та у
із умови рівності двох комплексних
чисел:
![]() .
.
Виділимо в обох частинах рівняння дійсні і уявні частини даних комплексних чисел:
![]()
Тепер, використовуючи рівності комплексних чисел, складемо систему:
![]()
розв’язавши
яку, одержуємо
![]() .
.
1.3. Геометричне зображення комплексного числа. Модуль та аргумент комплексного числа
В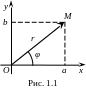 ізьмемо
на площині декартову прямокутну систему
координат
ізьмемо
на площині декартову прямокутну систему
координат
![]() (рис. 1.1) Домовимось комплексне число
зображати точкою
(рис. 1.1) Домовимось комплексне число
зображати точкою
![]() площини, абсциса якої у вибраній нами
декартовій прямокутній системі координат
дорівнює а,
а ордината – b.
Так між множиною всіх комплексних чисел
і сукупністю всіх точок площини
встановлюємо взаємно однозначну
відповідність: кожному комплексному
числу
відповідає одна і тільки одна точка
площини і, навпаки, кожна точка
площини, абсциса якої у вибраній нами
декартовій прямокутній системі координат
дорівнює а,
а ордината – b.
Так між множиною всіх комплексних чисел
і сукупністю всіх точок площини
встановлюємо взаємно однозначну
відповідність: кожному комплексному
числу
відповідає одна і тільки одна точка
площини і, навпаки, кожна точка
![]() відповідає одному і тільки одному
комплексному числу
.
Очевидно, комплексне число 0 зображається
точкою О
площини, яку взято як початок координат.
відповідає одному і тільки одному
комплексному числу
.
Очевидно, комплексне число 0 зображається
точкою О
площини, яку взято як початок координат.
Дійсні числа зображують
точками осі абсцис
![]() ,
яку називають в цьому випадку дійсною
віссю. Суто уявні числа
зображують точками осі ординат Oy,
тому цю вісь називають уявною.
Площину, між точками якої і комплексними
числами встановлено взаємно однозначну
відповідність, щойно описаним способом,
називають комплексною
площиною.
,
яку називають в цьому випадку дійсною
віссю. Суто уявні числа
зображують точками осі ординат Oy,
тому цю вісь називають уявною.
Площину, між точками якої і комплексними
числами встановлено взаємно однозначну
відповідність, щойно описаним способом,
називають комплексною
площиною.
Довільному комплексному
числу
ставимо у відповідність напрямлений
відрізок
![]() комплексної площини
,
початком якого є початок координат О,
а кінцем – точка М
з координатами
комплексної площини
,
початком якого є початок координат О,
а кінцем – точка М
з координатами
![]() .
Інакше, комплексному числу
ставимо у відповідність напрямлений
відрізок
,
що виходить з початку координат і
проекція якого на вісь абсцис дорівнює
а, а на
вісь ординат – b.
Числу 0 ставимо у відповідність точку
О –
початок координат. Так між множиною
всіх комплексних чисел і сукупністю
всіх напрямлених відрізків площини, що
виходять з початку координат , встановлено
взаємно однозначну відповідність.
Очевидно, кожному дійсному числу а
відповідає відрізок, що лежить на дійсній
осі, а всякому суто уявному числу
– відрізок, який лежить на уявній осі,
і навпаки. Зокрема, одиничним відрізкам,
що лежать на дійсній і уявній осях і
мають напрями цих осей, відповідають
числа 1 та і.
.
Інакше, комплексному числу
ставимо у відповідність напрямлений
відрізок
,
що виходить з початку координат і
проекція якого на вісь абсцис дорівнює
а, а на
вісь ординат – b.
Числу 0 ставимо у відповідність точку
О –
початок координат. Так між множиною
всіх комплексних чисел і сукупністю
всіх напрямлених відрізків площини, що
виходять з початку координат , встановлено
взаємно однозначну відповідність.
Очевидно, кожному дійсному числу а
відповідає відрізок, що лежить на дійсній
осі, а всякому суто уявному числу
– відрізок, який лежить на уявній осі,
і навпаки. Зокрема, одиничним відрізкам,
що лежать на дійсній і уявній осях і
мають напрями цих осей, відповідають
числа 1 та і.
Як бачимо, комплексні числа, так само як і дійсні, характеризують реальні об’єкти. Якщо дійсні числа описують величини, які зображуються напрямленими відрізками, розташованими на прямій, то комплексні числа характеризують більш складні й більш загальні величини, які зображуються напрямленими відрізками площини.
Модулем
комплексного числа
називається число
![]() ,
яке позначається r
або
,
яке позначається r
або
![]() ,
тобто
,
тобто
![]() (1.4)
(1.4)
Модуль комплексного числа
завжди є дійсне невід’ємне число:
![]() ,
причому
,
причому
![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли
![]() .
.
Із визначення модуля
комплексного числа випливає, що для
будь-яких комплексних чисел
![]() мають місце співвідношення:
мають місце співвідношення:
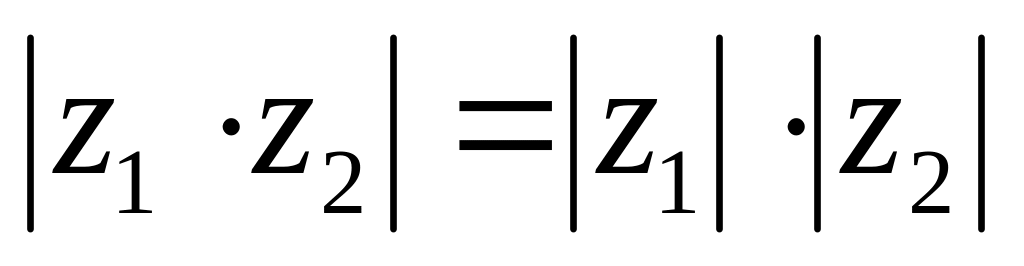 ;
;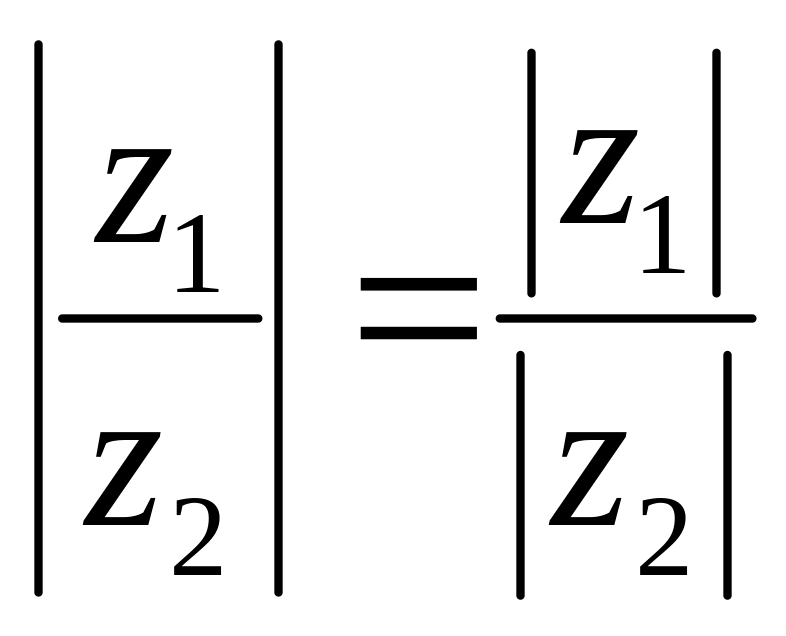 ,
якщо
,
якщо
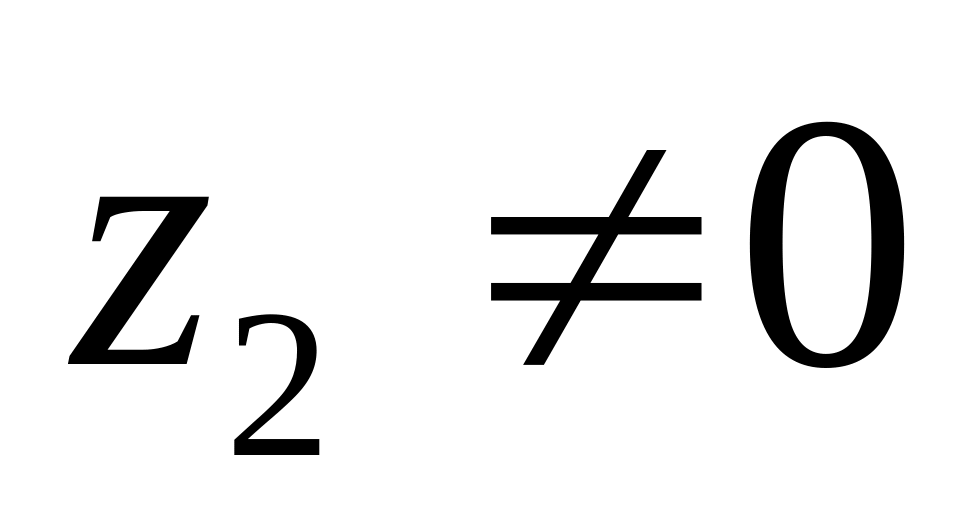 ;
;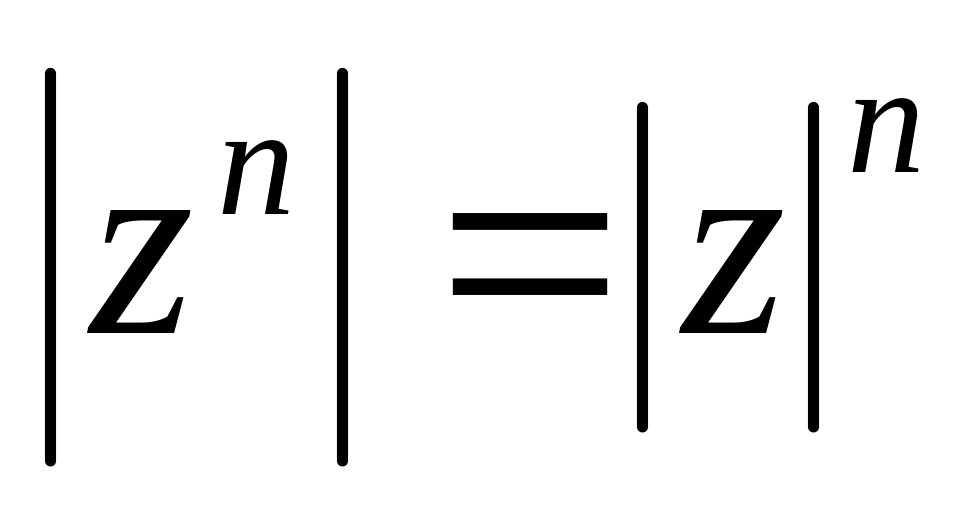 для будь-якого цілого числа
п (при
для будь-якого цілого числа
п (при
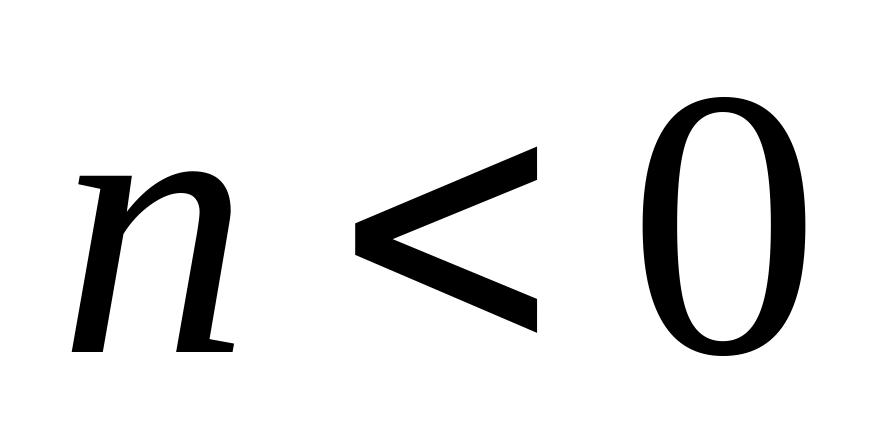 за умови, що
за умови, що
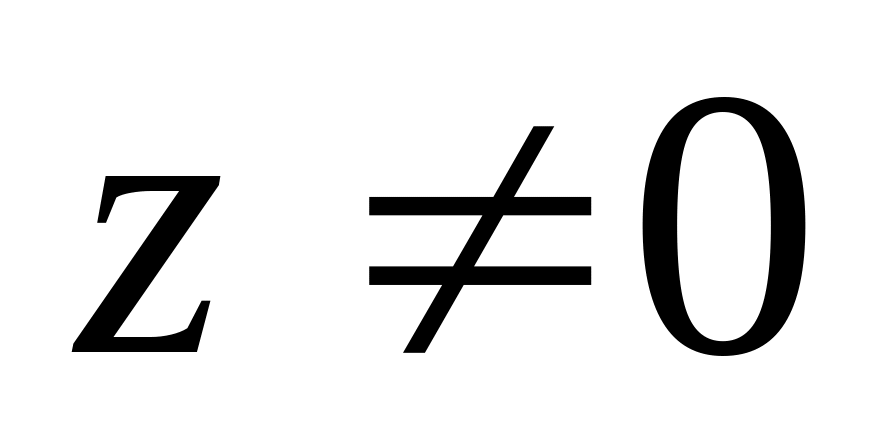 ).
).
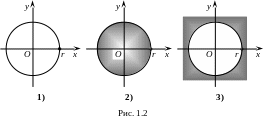
Якщо r – деяке додатне дійсне число, то на основі означення модуля комплексного числа одержуємо (див. рис. 5.2):
множина всіх чисел z, для яких
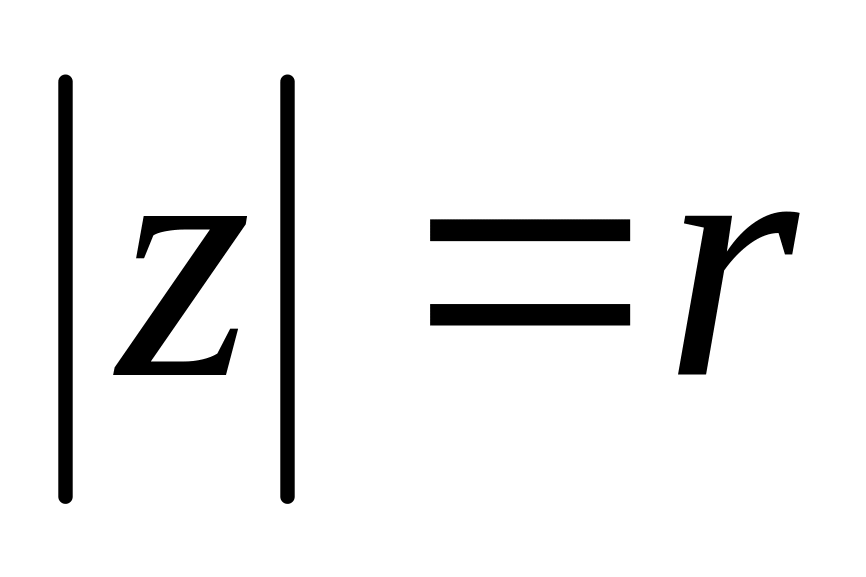 ,
являє собою коло радіусом r
з центром у початку координат;
,
являє собою коло радіусом r
з центром у початку координат;множина всіх чисел z, для яких
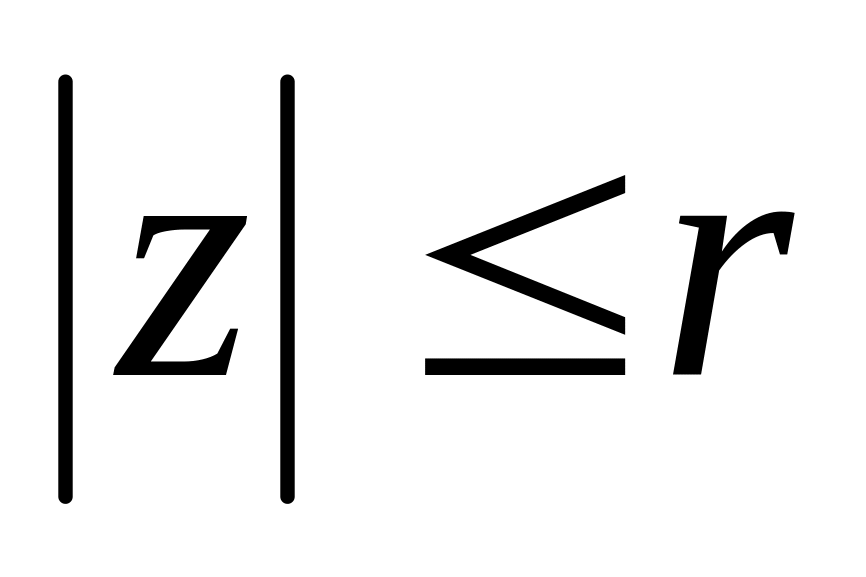 ,
являє собою круг радіусом r
з центром у початку координат;
,
являє собою круг радіусом r
з центром у початку координат;м
 ножина
всіх чисел z,
для яких
ножина
всіх чисел z,
для яких
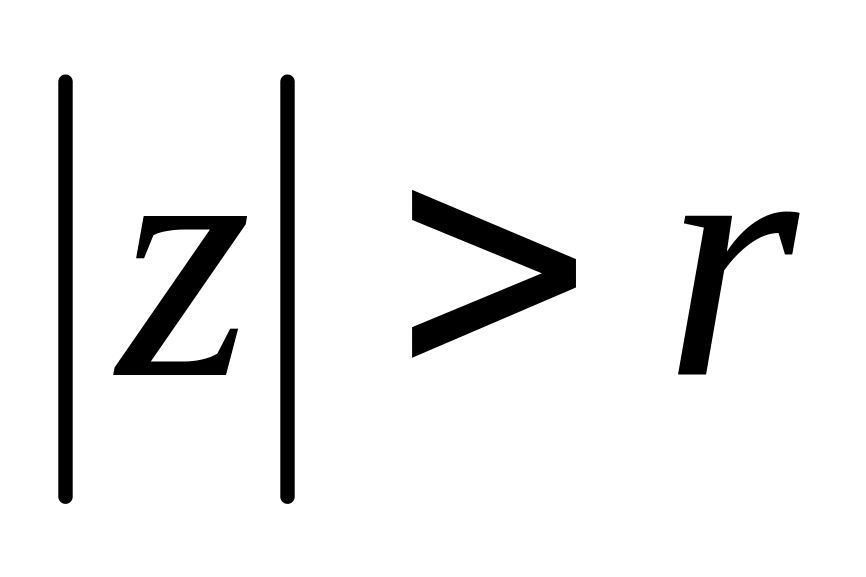 ,
являє собою зовнішню частину круга
радіусом r
з центром у початку координат.
,
являє собою зовнішню частину круга
радіусом r
з центром у початку координат.
Приклад.
1.8.
Визначити на комплексній площині
області, що задаються умовами: 1)
![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]() ;
4)
;
4)
![]() .
.
1) розв’язком є коло радіусу 5 з центром у початку координат;
2) розв’язком є круг радіусу 6 з центром у початку координат;
3)
розв’язком є круг радіусу 3 з центром
у точці
![]() ;
;
4)
розв’язком є кільце, обмежене колами
з радіусами 6 і 7 з центром в точці
![]() .
.
Із геометричної інтерпретації комплексного числа випливають наступні властивості:
Довжина вектора
 дорівнює
.
дорівнює
.Т
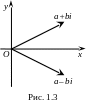
 очки
і
очки
і
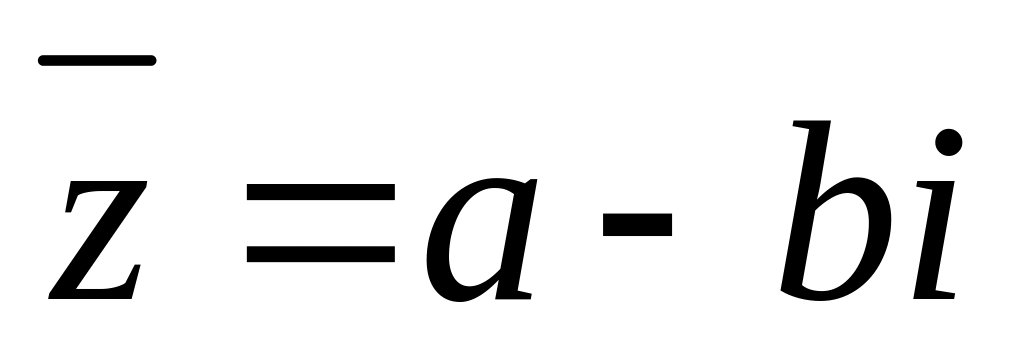 симетричні відповідно дійсної осі
(рис. 1.3).
симетричні відповідно дійсної осі
(рис. 1.3).Точки z і
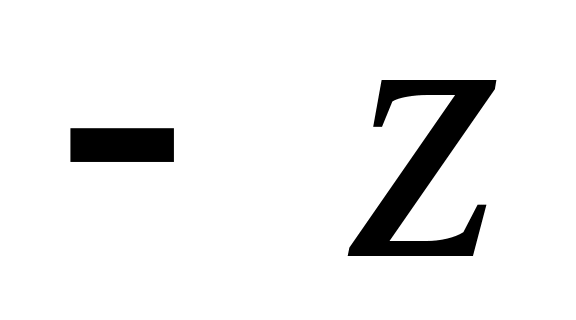 симетричні відносно точки
.
симетричні відносно точки
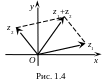
.Число
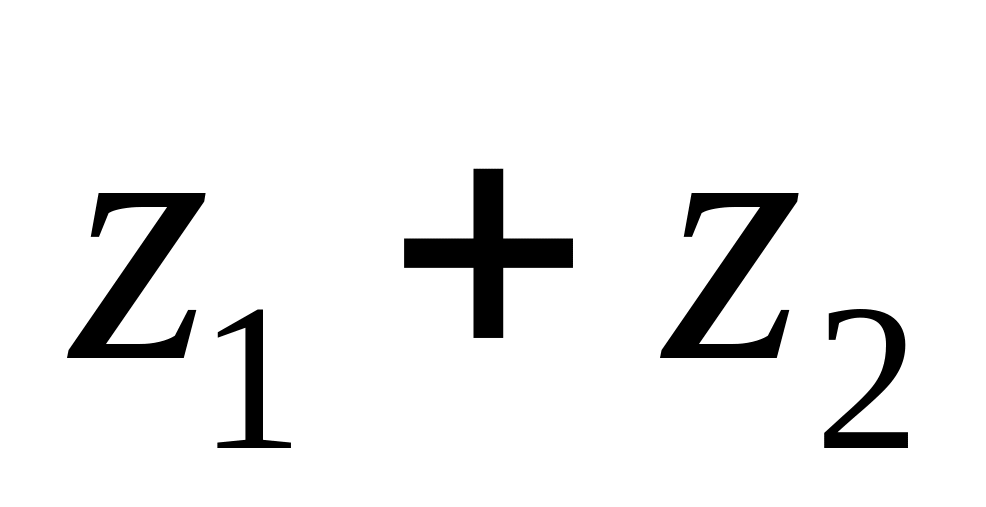 геометрично відображається як вектор,
який побудовано за правилом додавання
векторів, які відповідають точкам
і
(рис. 1.4).
геометрично відображається як вектор,
який побудовано за правилом додавання
векторів, які відповідають точкам
і
(рис. 1.4).Відстань між точками і дорівнює
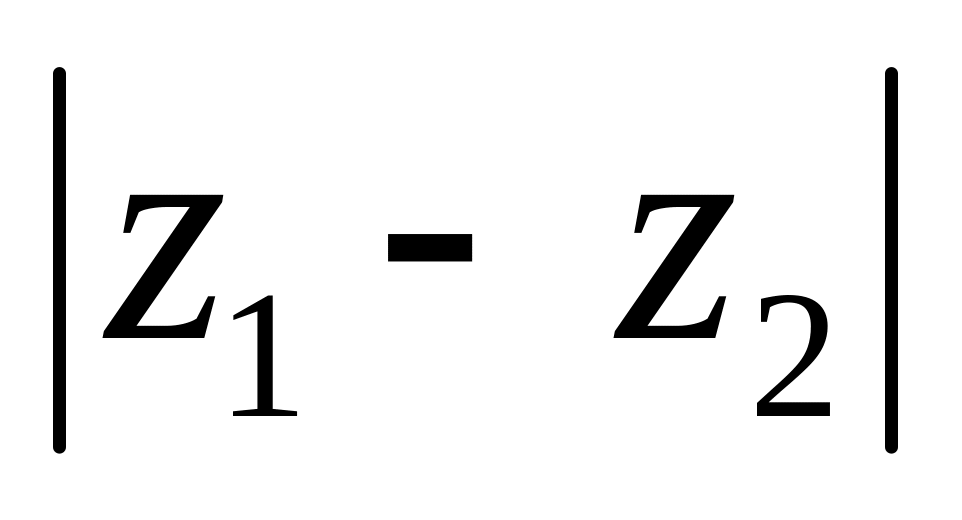 (рис. 1.5).
(рис. 1.5).
Кут
![]() між дійсною віссю
і вектором
між дійсною віссю
і вектором
![]() ,
що відраховується від додатного напрямку
дійсної осі, називається аргументом
комплексного числа
(див. рис. 1.1). Якщо відлік ведеться проти
руху годинникової стрілки, то величина
кута вважається додатною, а якщо за
рухом стрілки – від’ємною.
,
що відраховується від додатного напрямку
дійсної осі, називається аргументом
комплексного числа
(див. рис. 1.1). Якщо відлік ведеться проти
руху годинникової стрілки, то величина
кута вважається додатною, а якщо за
рухом стрілки – від’ємною.
Аргумент комплексного числа записується так:
![]() або
або
![]() (1.5)
(1.5)
Д ля
числа
аргумент не визначений.
ля
числа
аргумент не визначений.
Аргумент комплексного числа
визначається неоднозначно: будь-яке
комплексне число
має нескінчену множину аргументів, які
відрізняються один від одного на число,
кратне
![]() .
Найменше за абсолютною величиною
значення аргументу із проміжку
.
Найменше за абсолютною величиною
значення аргументу із проміжку
![]() називається головним
значенням аргументу.
називається головним
значенням аргументу.
Із означень тригонометричних
функцій випливає, що якщо
![]() ,
то мають місце рівності:
,
то мають місце рівності:
![]() (1.6)
(1.6)
С праведливе
і обернене твердження, тобто якщо
виконуються обидві рівності (5.6), то
.
Таким чином, всі значення аргументу
можна знайти, розв’язуючи разом рівняння
(1.6).
праведливе
і обернене твердження, тобто якщо
виконуються обидві рівності (5.6), то
.
Таким чином, всі значення аргументу
можна знайти, розв’язуючи разом рівняння
(1.6).
Алгоритм знаходження
значення аргументу комплексного числа
![]() :
визначити, в якій чверті
знаходиться точка
(використати геометричну інтерпретацію
числа
);
знайти в цій чверті кут
,
розв’язавши одне із рівнянь (5.6) або
рівняння
:
визначити, в якій чверті
знаходиться точка
(використати геометричну інтерпретацію
числа
);
знайти в цій чверті кут
,
розв’язавши одне із рівнянь (5.6) або
рівняння
![]() (1.7)
(1.7)
та знайти всі значення
аргументу числа z за формулою
![]()
Приклади.
1.9.
Побудувати радіус-вектори, які відповідають
комплексним числам: 1)
![]() ;
2)
;
2) ![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() .
.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5) ![]() (рис. 1.6).
(рис. 1.6).
1.10.
Знайти модуль і головне значення
аргументу комплексних чисел: 1) ![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
1)
Оскільки
![]() .,
то за формулою (5.4) отримаємо
.,
то за формулою (5.4) отримаємо
![]() ;
при цьому
;
при цьому
![]() ,
тому що вектор, який відображає дане
число, належить додатній вісі Oy;
,
тому що вектор, який відображає дане
число, належить додатній вісі Oy;
2)
![]() ;
знаходимо
;
знаходимо
![]() ;
так як вектор, який відображає дане
число, лежить на від’ємній вісі Oy,
то
;
так як вектор, який відображає дане
число, лежить на від’ємній вісі Oy,
то![]() ;
;
3)
так як
![]() ,
точка, яка відображає дане число, лежить
в І чверті, значить,
,
точка, яка відображає дане число, лежить
в І чверті, значить,
![]() ;
;
![]() ;
;
![]() ;
;
4)
оскільки
![]() ,
то точка, яка відображає дане число,
лежить в ІV чверті, отже,
,
то точка, яка відображає дане число,
лежить в ІV чверті, отже,
![]() ,
значить,
,
значить,
![]() і
і
![]() .
.
