Уравнения эвольвенты

Уравнение эвольвенты удобнее представлять не в прямоугольной (Декартовой) системе координат, а в полярной. Для этого необходимо для определения положения любой точки эвольвенты определить радиус-

вектор точки. В нашем случае необходимо знать длину радиуса r_х и угловую координату от точки А₀ - начала эвольвенты.

Обозначим угол между радиусом, идущим в начало эвольвенты А₀ и радиусом, идущим в точку а₁ - inv x (inv - зависящий, сопутствующий - англ.). Установим зависимость между углами _x и inv _x. Сум­ма углов _х и inv _x в радианах равна дуге основной окружности А₀В₀ (рис. 8).

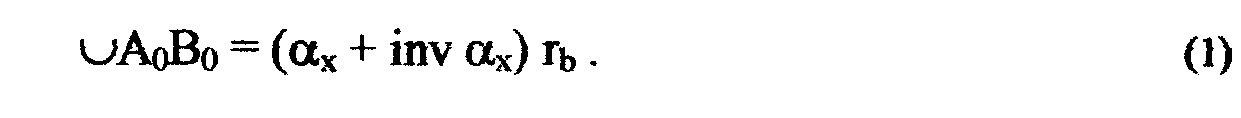
[3]

Дуга основной окружности А₀В₀ равна отрезку нормали а₁в₀. Отрезок а₁в₀ определим из прямо­угольного треугольника а₁в₀O.

[4]

Приравниваем правые части равенств [3] и [4]

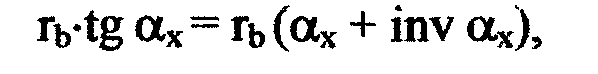
откуда получаем первое уравнение эвольвенты

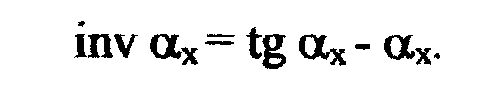
Из этого же треугольника получаем второе уравнение

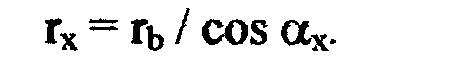
По этим двум уравнениям можно определить положение любой точки эвольвенты, имея радиус основ­ной окружности r_b и задаваясь значениями углов _x.

Поскольку между углами _x и inv _x существует аналитическая зависимость, то с целью облегчения расчетов составлены таблицы, как и для определения тригонометрических функций.