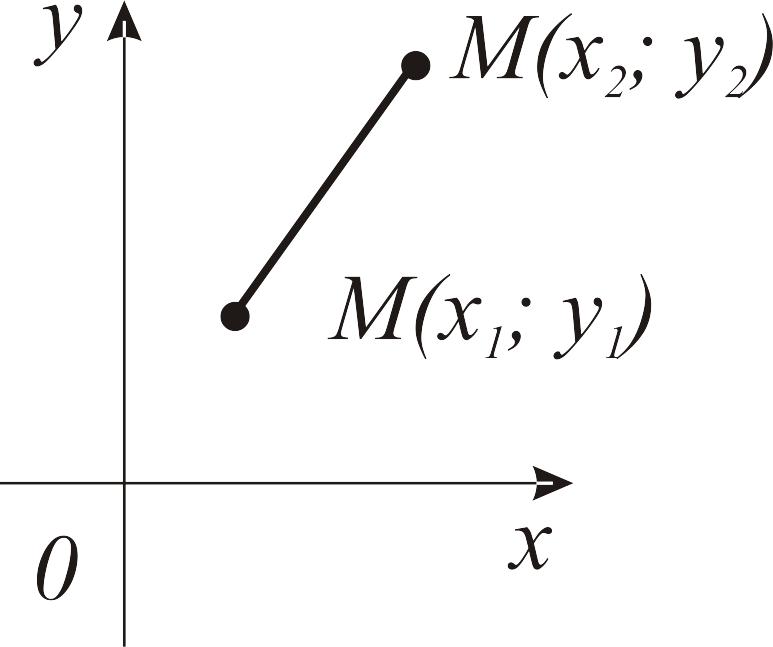3. Аналитическая геометрия

В аналитической геометрии изучают пространственные отношения и формы тел [2, гл. III, IV] с помощью метода координат, создателем которого считают французского математика Рене Декарта. В основе метода координат находятся координаты и координатные системы.

3.1. Системы координат

Системой координат на плоскости или в пространстве называют систему, состоящую из точек, прямых, лучей, векторов, кривых или других элементов плоскости или пространства, по отношению к которой можно охарактеризовать положение тела (точки) с помощью чисел. Упорядоченную совокупность чисел, с помощью которой определяется положение точки относительно системы координат, называют координатами точки относительно выбранной системы.

Наиболее простой и часто используемой оказалась декартова прямоугольная система координат, которую изучают в школьном курсе математики [2, гл. III, § 9].

На плоскости, кроме прямоугольной системы координат, важную роль для практики играет полярная система координат [2, гл. III, § 9].

Полярная система координат определяется точкой 0, лучом ОР и масштабной единицей ОЕ = 1. В этой системе координат (рис. 1) точку М определяют с помощью двух чисел r и φ (координат)

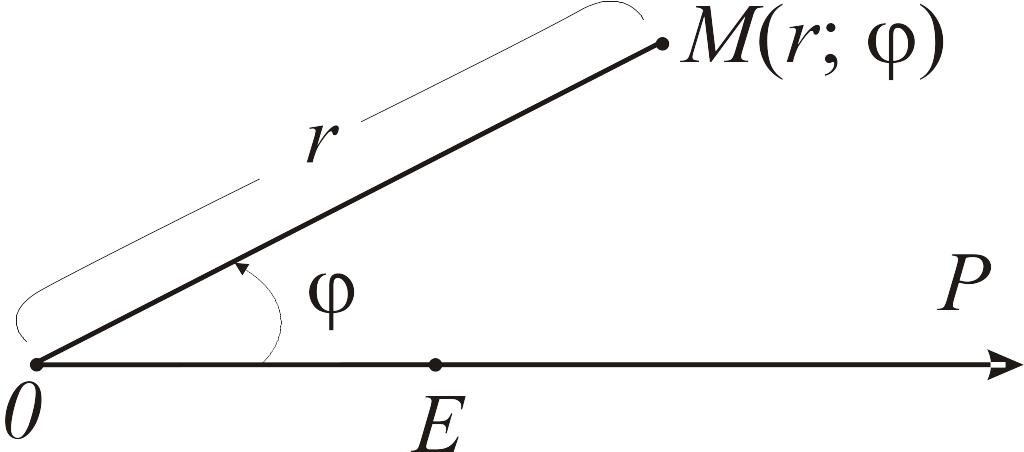
Рис. 1. Изображение полярной системы координат:

0 — полюс; ОР — полярная ось; ОЕ — масштабная единица;

r = ОМ — полярный радиус точки М;

φ = (ОР,^ ОМ) — полярный угол точки М;

r, φ — полярные координаты точки М

Обычно полагают, что r ≥ 0, –  φ  . Построение точки в полярной системе координат начинают с построения луча под углом φ, а затем — отрезка ОМ.

Пример 10. Построить в полярной системе координат точки:

А(2; ); В(2; ); С(2; ); Д(2; 0).

Решение

Построение точек покажем на рис. 2.

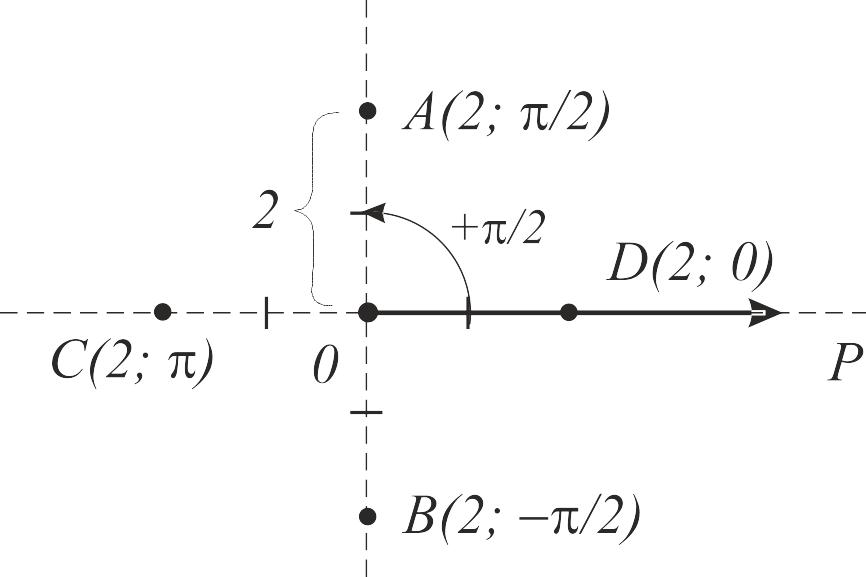
Рис. 2. Изображение точек в полярной системе координат

3.2. Простейшие задачи на метод координат

Простейшими задачами на метод координат считают: определение расстояния между двумя точками и деление отрезка в заданном отношении. Решаются эти задачи проще в прямоугольной системе координат.

1. Расстояние между двумя точками:

	. (11)
Рис. 3. Расстояние между двумя точками d = М1М2

Замечание. В пространстве добавляется еще одна, третья координата z и формула (11) принимает следующий вид:

.

2. Деление отрезка в заданном отношении.

Пусть точка М делит отрезок М₁М₂ в отношении , т.е. так, что

М1М / ММ2 = .

Тогда координаты точек М(x; y), М₁(x₁; y₁), М₂(x₂; y₂) связаны соотношениями

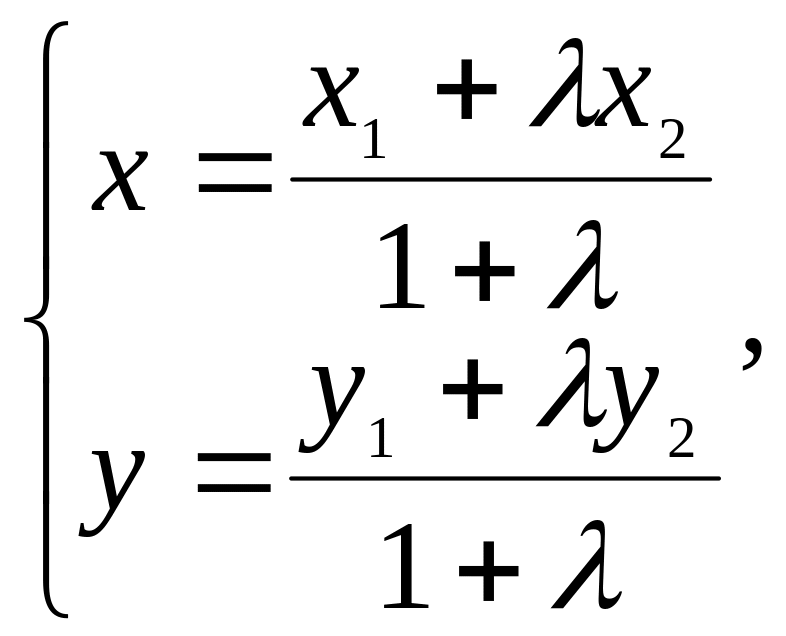(12)

а при  = 1 соотношениями

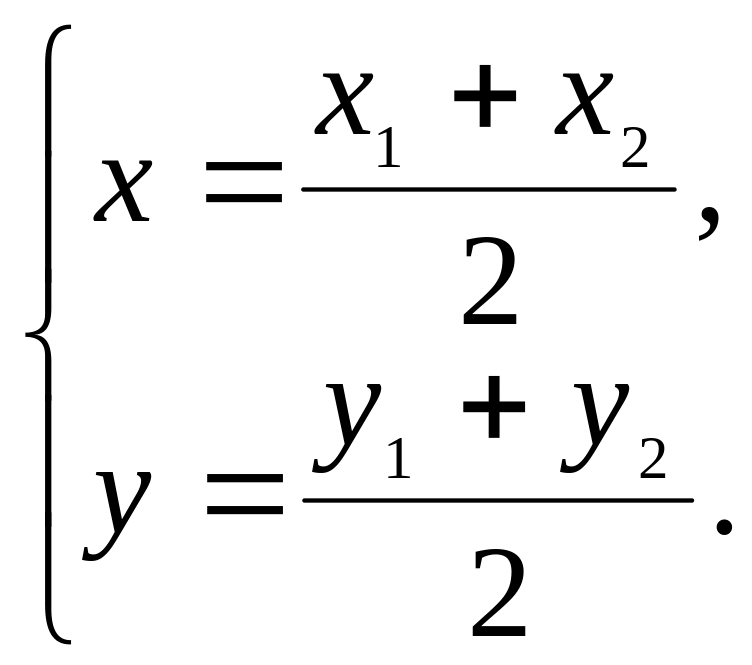(13)

Примечание. При рассмотрении этой задачи в пространстве в формулах (12), (13) добавляется аналогичное равенство для z.

Пример 11. Даны вершины треугольника А(0; –3), В(1; –1), С(5; 3). Найти длину стороны ВС и длину медианы АД.

Решение

Длину стороны ВС найдем по формуле (11), взяв за первую точку точку В, а за вторую — точку С.

Для определения длины медианы АД найдём сначала координаты точки Д. Так как точка Д делит отрезок ВС пополам, то по формуле (13) находим

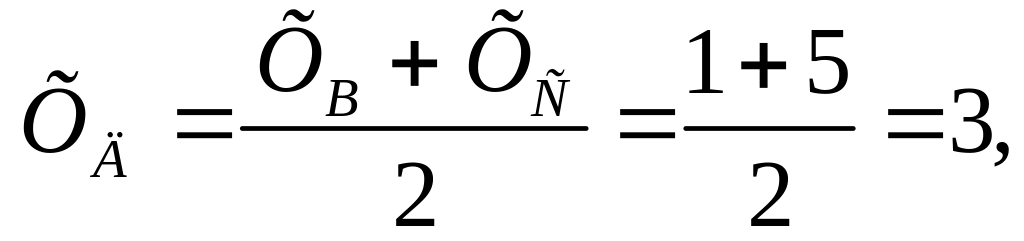
Следовательно, точка Д (3;1). А теперь снова по формуле (11) находим

Таким образом,