6.8. Условия механического равновесия твердого тела

Условия равновесия твердого тела, как и материальной точки, представляет собой частный случай динамических уравнений, когда ускорения тела равны нулю. Твердое тело может совершать три независимых поступательных движения вдоль трех координатных осей X, Y, Z вместе с центром масс и три независимых вращательных движения относительно этих координатных осей. Отсюда следует, что для того чтобы твердое тело оставалось неподвижным (находилось в равновесии) все указанные движения должны быть исключены. Чтобы исключить поступательные движения вдоль осей, необходимо, чтобы сумма проекций этих сил на соответствующие координатные оси должна быть равна нулю:

(6.15)

Аналогично, чтобы исключить вращение тела вокруг координатных осей должна быть равна нулю сумма проекций моментов внешних сил относительно этих осей:

6.16) Напомним, что знак момента силы относительно оси определяется выбором положительного направления вращения (по или против часовой стрелки). Если данная сила вызывает вращение в положительном направлении, то ее момент берется со знаком плюс, если в противоположном, – со знаком минус.

Равенства (6.15) и (6.16) и определяют условия равновесия твердого тела.

В качестве примера применения условий равновесия рассмотрим сложение двух параллельных сил F₁ и F₂, приложенных к телу в точках А и В (рис. 6). Параллельными силами называются такие силы, линии действия которых параллельны друг другу. Если линии действия сил пересекаются в одной точке, силы называются сходящимися.

Направим ось X системы координат XYZ вдоль линии АВ, а ось Y – вдоль направления вектора F₁. Тогда проекция каждой силы на ось X будет равна нулю, вследствие чего первое уравнение (6.15) обращается в тождество, а поскольку все силы лежат в плоскости XY (плоская система сил), то и третье уравнение (6.15) обращается в тождество. В данной системе сил вращение может происходить только вокруг оси Z, поэтому и первое и второе уравнения (6.16) превращаются в тождество. В результате для указанной системы сил остаются два условия равновесия:

Чтобы данная система сил находилась в равновесии, к телу следует приложить еще уравновешивающую силу, направив ее вертикально вверх. Обозначим ее через F_y. Тогда из первого условия равновесия с учетом направления уравновешивающей силы получим Откуда F_y = F₁ + F₂. Равнодействующая R сил F₁ и F₂ направлена противоположно уравновешивающей силы, т.е. по направлению сил F₁ и F₂, так что

Чтобы найти точку приложения C равнодействующей силы воспользуемся условием равновесия для моментов. Сумма моментов двух сил относительно оси, проходящей через точку C и параллельной оси Z должна быть равна нулю. С учетом знаков для M₁ M₂, находим где – расстояние между точками А и В, x – расстояние между точками А и С. Откуда

Это есть расстояние точки приложения равнодействующей от линии действия силы F₁ (x-координата точки приложения).

Если силы направлены в разные стороны, то они имеют противоположные знаки и равнодействующая равна разности этих сил: А x-координата ее точки приложения

Из этой формулы видно, что если F₁ > F₂, то x < 0. Это значит, что точка приложения силы R лежит левее точки приложения силы F₁.

Пусть теперь две силы F₁ и F₂ равны по величине и противоположны по направлению. В этом случае R = 0, а x . Это означает, что две равные антипараллельные силы, линии действия которых не совпадают нельзя заменить одной силой. Такая система двух равных по модулю и противоположно направленных сил, не лежащих на одной прямой, называется парой сил. Действие пары сил нельзя свести к действию одной силы, ее нельзя уравновесить одной силой. Однако эти силы не уничтожают друг друга. Особенность такой пары сил состоит в том, что она не при

Рис. 9

водит к поступательному движению, так как R = 0. Тем не менее, она оказывает весьма существенное действие на тело – вращает его. Вращающее действие пары сил измеряется ее моментом, равным произведению модуля любой из сил на плечо пары – на расстояние между линиями действия сил пары.

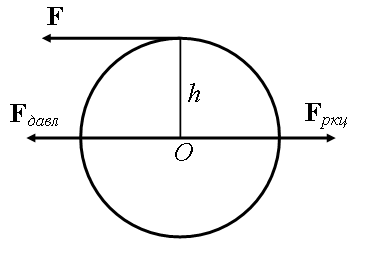
Рассмотрим, например, диск, который может свободно вращаться вокруг оси О, перпендикулярной диску. Если к точке А на ободе диска приложить силу F, направив ее по касательной к боковой поверхности диска (направленная таким образом сила, называется окружным усилием, рис. 6.), то диск станет вращаться. Вращение диска обусловлено появлением пары сил. Сила F, действуя на диск, прижимает его в точке О к оси (сила F_давл на рис. 6. приложена к оси О) и возникает реакция оси F_ркц, приложенная так же, как и сила F, к диску. Так как все эти силы равны по модулю и линии их действия параллельны, то силы F и F_ркц образуют пару сил, которая и приводит диск во вращение.