температура охладителя. Обычно охладителем является окружающий воздух, температуру которого понизить не представляется возможным, поэтому для увеличения КПД стараются увеличить температуру нагревателя.

Более общий анализ показывает, что КПД машины Карно не зависит от физической природы рабочего тела и определяется той же формулой (5.20).

Холодильная машина, работающая по циклу Карно, как легко убедиться с учетом формулы (5.21), имеет холодильный коэффициент

Здесь T₁ – температура окружающей среды, T₂ – температура холодильной камеры. Видим, что холодильный коэффициент тем больше, а, значит, работа холодильной машины тем эффективнее, чем меньше разность между температурами окружающей среды и холодильной камеры.

Глава 6

ВТОРОЕ И ТРЕТЬЕ НАЧАЛА ТЕРМОДИНАМИКИ

6.1. Энтропия. Энтропия идеального газа

На основе анализа работы тепловых машин Р. Клаузиус установил, что для всех круговых процессов имеет место неравенство

(6.1)

Кружок у символа интеграла означает, что интегрирование проводится по круговому процессу. Строгое равенство в (6.1) имеет место для равновесных круговых процессов, а строгое неравенство – для неравновесных. Соотношение (6.1) называют неравенством Клаузиуса.

Рассмотрим сначала равновесные круговые процессы. В этом случае

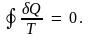(6.2)

На равенстве (6.2) основано введение фундаментального в термодинамике понятия энтропии. Убедимся в справедливости этого равенства на примере цикла Карно (рис.5.8). Имеем

так как процессы 12 и 34 – изотермические, а процессы 23 и 41 – адиабатические. Учитывая, что для цикла Карно, как это следует из формулы (5.18), члены в правой части равны друг другу, приходим к равенству (6.2). Любой равновесный круговой процесс можно разбить на ряд элементарных циклов Карно (способом, показанным на рис. 6.1). Для каждого элементарного цикла выполняется равенство (6.2), и поэтому оно будет справедливо для любого равновесного кругового процесса.

В математике доказывается, что если криволинейный интеграл

Рис. 6.1

по любому замкнутому контуру равен нулю, то его подынтегральное выражение представляет полный дифференциал некоторой функции. Применяя эту теорему к криволинейному интегралу, стоящему в правой части равенства (6.2), можно записать

(6.3)

где 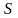– некоторая функция. Эту функцию называют энтропией термодинамической системы. Утверждение о существовании функции, дифференциал которой определяется равенством (6.3), носит название принципа существования энтропии.

Найдем энтропию идеального газа. С учетом уравнения состояния идеального газа будем иметь

Тогда получим

где 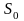– произвольная постоянная. Отсюда получаем энтропию идеального газа:

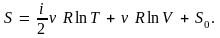(6.4)

На примере идеального газа видно, что энтропия является функцией состояния термодинамической системы (зависит от параметров состояния, в случае газа – от T и V).

Энтропия является аддитивной величиной, т.е. энтропия системы равна сумме энтропий отдельных ее частей: S = S₁ + S₂ + + S₃ + … Это вытекает из того, что энергия системы U и работа, совершаемая системой A, аддитивны. Тогда из первого закона термодинамики в форме (5.10) следует, что аддитивна и теплота Q, а значит, аддитивна и энтропия S.

Из равенства (6.3) находим, что 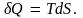Это равенство представляет собой общее определение количества теплоты, получаемой или отдаваемой системой при бесконечно малом равновесном изменении состояния. При конечном изменении состояния

При адиабатном процессе и, следовательно, откуда S = const. Таким образом, адиабатный процесс также является изопроцессом – изоэнтропийным.

Проинтегрировав обе части равенства (6.3) в пределах между двумя состояниями 1 и 2, найдем изменение энтропии при переходе системы между этими состояниями:

(6.5)

Пределы интегрирования 1 и 2 в каждом конкретном случае зависят от явного вида выражения, определяющего 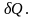В изотермическом процессе Смысл этого соотношения состоит в

Рис. 6.2

том, что если в изотермическом процессе системе передается количество теплоты Q, то ее энтропия возрастает на ∆S.

Наличие произвольной постоянной показывает, что энтропия определяется неоднозначно, а с точностью до аддитивной постоянной. Для придания энтропии однозначности в некотором произвольном состоянии О ее принимают равной некоторому наперед заданному значению . Тогда энтропия в других состояниях α будет определяться с помощью равенства (6.5), если положить в нем а

Найдем теперь изменение энтропии при неравновесном процессе перехода системы из состояния 1 в состояние 2. Для этого образуем круговой процесс, причем из состояния 2 обратно в состояние 1 вернемся с помощью равновесного процесса (рис. 6.2, неравновесный процесс на этом рисунке изображен пунктиром). Полученный замкнутый цикл в целом будет неравновесным, так как неравновесной является одна из его частей (12), и тогда

где учтено, что для процесса 21 в соответствии с формулой (6.5) интеграл в пределах 21 равен S₁ – S₂. Откуда получаем для неравновесного процесса перехода системы из состояния 1 в состояние 2:

Объединяя это неравенство с равенством (6.5), в общем случае будем иметь

(6.6)

где, как и в (6.1), строгое равенство имеет место для равновесного процесса, а строгое неравенство – для неравновесного. Для бесконечно малого изменения состояния

, (6.7)

или Объединяя это неравенство с первым законом термодинамики, получим

(6.8)

Соотношение (6.8) называется основным термодинамическим неравенством. Соотношение

называется основным термодинамическим тождеством. Оно объединяет первый и второй законы термодинамики и справедливо для бесконечно малых равновесных процессов.