6.7. Энтропия и информация

С развитием теории информации выяснилось, что понятие энтропии допускает более широкое статистическое толкование, чем просто степень беспорядка молекулярной системы. Это связано с тем, что вытекающая из формулы Больцмана формула (6.12) связывает величины разной природы – физической S и математической p. Этим и объясняется широкое применение формулы Больцмана и связанных с нею термодинамических представлений не только в физике, но и в других науках, которые пользуются понятием вероятности, в частности в теории информации, лежащей в основе современной кибернетики. Связь между энтропией и информацией – еще одно важное следствие второго начала термодинамики. Под информацией понимаются любые сведения, переданные от одного субъекта (или объекта) к другому посредством звуковых, световых, печатных, цифровых или другого вида сигналов.

К. Шеннон ввел понятие информационной энтропии, которая выступает как мера неопределенности при характеристике объекта или явления и базируется на вероятностном подходе. Пусть M – число возможных событий, исходов; число реализаций какой-либо ситуации; число вариантов и т.п. По Шеннону информационная энтропия связана с числом возможных исходов так же, как энтропия термодинамическая связана со статистическим весом, т.е. логарифмической зависимостью

(6.17)

где K – некоторый коэффициент пропорциональности.

. Анализ выражения (6.17) позволяет сделать следующие выводы: информационная энтропия 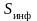монотонно возрастает с увеличением числа исходов M. Это соответствует тому, что чем больше число возможных исходов, тем неопределеннее ситуация. Если M = 1, то 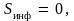т.е. неопределенность отсутствует, результат строго детерминирован.

Количество информации I, полученное в опыте или при передаче сигналов, характеризуется устранимой при этом неопределенностью. Поэтому под информацией следует понимать не любое сообщение, а только то, которое устраняет (уменьшает) неопределенность. Все остальное – это информационный шум. За количество информации принимают уменьшение неопределенности, т.е. величину

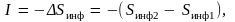
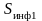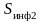где – информационная энтропия (неопределенность) до опыта, – информационная энтропия (неопределенность) после опыта. А поскольку 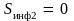(ситуация выяснилась, и поэтому неопределенность исчезла), то 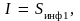т.е. количество информации равно первоначальному значению неопределенности:

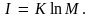
Постоянная K остается произвольной; ее численное значение может быть найдено с помощью некоторого определения. Обычно используется следующее определение. Рассмотрим так называемую двоичную систему, которая имеет только два исхода (M = 2), и потребуем, чтобы 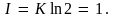Отку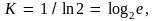да тогда

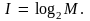
Информация, полученная при реализации одного из двух исходов, называется информацией в 1 бит. Поэтому определенная формулой информация измеряется в битах. Так, если M = 8 = 2³, то I = 3 бит. Если M = 1, то I = 0, что соответствует случаю, когда информация отсутствует. Единица измерения информации бит в равной мере пригодна для исследования всех видов информационных процессов. Благодаря ее введению наука приобрела инструмент для исследования информационно-энтропийных соотношений, справедливых для всех форм информации.

Часто информацию измеряют в единицах, называемых натами (от термина «натуральный логарифм»). В этом случае полагают K = 1 и тогда

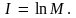
Если все исходы равновероятны, то вероятность каждого исхода 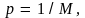откуда 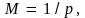а информационная энтропия

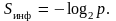
Определенная таким образом информационная энтропия в теории информации выступает как мера неожиданности события. Эта формула хорошо передает многие из наших интуитивных представлений о свойствах, которыми она должна обладать. Действительно, вероятность есть величина, меньшая единицы, и, следовательно, ее логарифм, взятый со знаком минус, есть величина положительная, а значит, положительной величиной является и неожиданность. Чем меньше вероятность реализации какого-либо события, тем оно неожиданнее и тем, следовательно, больше 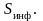Если событие достоверно, то вероятность равна единице, а ее логарифм равен нулю.

Уменьшение неожиданности, являющееся следствием измерения (наблюдения) можно принять в качестве меры информации, которая при этом была получена. Так как конечная неопределенность равна нулю, то уменьшение неожиданности равно ее первоначальному значению. Поэтому выражение 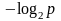является также мерой количества информации, полученной в опыте, который показывает, что событие А осуществилось. Таким образом,

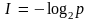
или

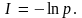
Если рассматривается некоторая полная группа неожиданных событий, каждое из которых обладает своей неожиданностью, то возникает вопрос о характеристике, общей для всей системы. Такой характеристикой является информационная энтропия, которая вводится теперь как среднее по всей системе значение неожиданностей, т.е. неожиданность каждого i-го события 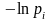умножается на вероятность этого события 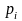, и все полученные результаты суммируются. Таким образом,

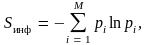(6.18)

причем

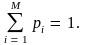(6.19)

Суммирование в выражениях (6.18) и (6.19) распространяется на все события, составляющие полную группу. Энтропия характеризует степень неопределенности или хаотичности, которая имеет место в данной ситуации. Заметим, что величина равна нулю, если какое-либо из p_j равно единице, а все остальные p_i равны нулю, т.е. когда результат испытания может быть предсказан с достоверностью и неопределенность в информации отсутствует. 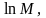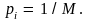Можно показать (используя метод множителей Лагранжа), что максимального значения, равного информационная энтропия достигает, когда все Очевидно, что этот предельный случай обладает наибольшей неопределенностью.

Для распределения вероятности непрерывной величины x с плотностью f (x) информационная энтропия равна

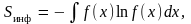
при этом