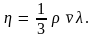4.5. Внутреннее трение в газах
Внутреннее трение, или вязкость, – это явление, возникающее между соприкасающимися слоями газа. Механизм его заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями газа, в результате чего импульс слоя, движущегося быстрее, уменьшается, а слоя, движущегося медленнее, увеличивается. Это приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.
Сила внутреннего трения между двумя слоями газа подчиняется закону Ньютона:
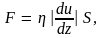
где
 – динамическая
вязкость (вязкость);
– динамическая
вязкость (вязкость);
 – градиент скорости,
показывающий быстроту изменения скорости
в направлении оси Z,
перпендикулярной направлению движения
слоев; S
– площадь, на которую действует сила
F.
– градиент скорости,
показывающий быстроту изменения скорости
в направлении оси Z,
перпендикулярной направлению движения
слоев; S
– площадь, на которую действует сила
F.
Взаимодействие
двух слоев согласно второму основному
закону динамики можно рассматривать
как процесс, при котором от одного слоя
к другому за единицу времени переносится
импульс, по величине равный действующей
силе:
 Учитывая, что
Учитывая, что
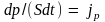 –
плотность потока импульса – величина,
численно равная полному импульсу,
переносимому за единицу времени в
положительном направлении оси Z,
формулу Ньютона приведем к виду
–
плотность потока импульса – величина,
численно равная полному импульсу,
переносимому за единицу времени в
положительном направлении оси Z,
формулу Ньютона приведем к виду
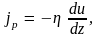
где знак минус учитывает то обстоятельство, что импульс переносится в направлении убывания скорости.
Пусть 1 и 2 – два
соприкасающихся слоя, движущихся в
потоке газа со скоростями u1
и u2
– скорости упорядоченного движения.
Переходя из слоя 1 в слой 2 со скоростью
вследствие теплового движения, молекулы
первого слоя переносят во второй импульс
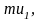 а молекулы второго слоя при переходе в
первый – импульс
а молекулы второго слоя при переходе в
первый – импульс
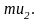 Проведя выкладки, подобные тем, которые
были проведены при расчете коэффициента
теплопроводности, и заменив при этом
на импульс mu,
для плотности потока импульса будем
иметь
Проведя выкладки, подобные тем, которые
были проведены при расчете коэффициента
теплопроводности, и заменив при этом
на импульс mu,
для плотности потока импульса будем
иметь
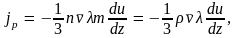 (4.6)
(4.6)
где учтено, что
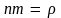 –
плотность газа.
–
плотность газа.
Сравнивая выражение (4.6) с экспериментальным выражением плотности потока импульса, получим коэффициент вязкости
|
(4.7) |
Сравнивая выражения
(4.4), (4.5) и (4.7) для коэффициентов
соответственно диффузии D,
теплопроводности
и вязкости
 получим следующие соотношения между
этими коэффициентам:
получим следующие соотношения между
этими коэффициентам:
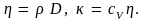
Как видно из формул (4.4), (4.5), (4.7) все три коэффициента (диффузии, теплопроводности и вязкости) зависят от средней длины свободного пробега молекул газа. Поэтому из опытов по диффузии, теплопроводности или вязкости газа можно определить 𝜆 и по формуле (4.2) вычислить эффективный диаметр молекул.