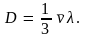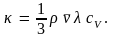4.3. Диффузия в газах
Явление диффузии наблюдается, когда в смеси газов концентрация какого-либо газа распределена неравномерно. В этом случае возникает перенос этого газа в места с меньшей концентрацией. Если в сосуде находится только один газ, плотность которого в занимаемом им объеме неодинакова, то происходит проникновение молекул газа в части объема, где плотность газа меньше. Это явление называется самодиффузией.
Явление диффузии для химически однородного газа (самодиффузия) подчиняется экспериментальному закону Фика:

где
 – плотность потока массы – величина,
численно равная массе вещества,
переносимой за единицу времени через
единичную площадку, перпендикулярную
оси X, D
– величина,
называемая диффузией (коэффициентом
диффузии),
– плотность потока массы – величина,
численно равная массе вещества,
переносимой за единицу времени через
единичную площадку, перпендикулярную
оси X, D
– величина,
называемая диффузией (коэффициентом
диффузии),
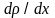 – градиент плотности, определяющий
скорость (быстроту) изменения плотности
газа в направлении оси X.
Знак минус показывает, что пере-
– градиент плотности, определяющий
скорость (быстроту) изменения плотности
газа в направлении оси X.
Знак минус показывает, что пере-
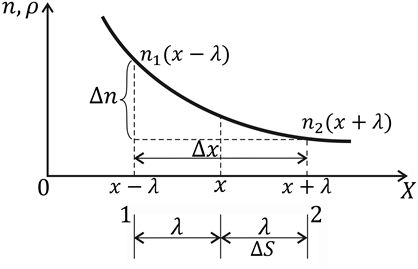
Рис. 4.2 |
Предположим,
что концентрация n
газа изменяется вдоль оси x
(рис.4.2) и описывается функцией
 Выделим в газе некоторую площадку
Выделим в газе некоторую площадку
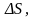 перпендикулярную оси X.
За единицу времени через эту площадку
вследствие теплового движения пройдет
некоторое количество молекул справа
налево и обратно слева направо. Поскольку
концентрации молекул по обе стороны от
площадки различны, то в одном направлении
молекул будет проходить больше, чем в
противоположном. Вследствие чего
возникает поток массы через эту площадку.
Возьмем два слоя 1 и 2, параллельных
площадке
на расстояниях средней длины свободного
пробега молекул
слева и справа от этой площадки. Через
указанную площадку пролетают те молекулы,
которые претерпели последнее соударение
друг с другом в среднем на расстоянии
от этой площадки. Пусть n1
и n2
– значения концентрации молекул в слоях
1 и 2 соответственно. Если
перпендикулярную оси X.
За единицу времени через эту площадку
вследствие теплового движения пройдет
некоторое количество молекул справа
налево и обратно слева направо. Поскольку
концентрации молекул по обе стороны от
площадки различны, то в одном направлении
молекул будет проходить больше, чем в
противоположном. Вследствие чего
возникает поток массы через эту площадку.
Возьмем два слоя 1 и 2, параллельных
площадке
на расстояниях средней длины свободного
пробега молекул
слева и справа от этой площадки. Через
указанную площадку пролетают те молекулы,
которые претерпели последнее соударение
друг с другом в среднем на расстоянии
от этой площадки. Пусть n1
и n2
– значения концентрации молекул в слоях
1 и 2 соответственно. Если
 – средняя скорость хаотического
теплового движения, то слева направо
через площадку
пройдут за время
– средняя скорость хаотического
теплового движения, то слева направо
через площадку
пройдут за время
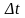 все молекулы, движущиеся в направлении
оси x > 0,
а справа налево – в направлении оси x
< 0. Эти молекулы
находятся в слоях толщиной
все молекулы, движущиеся в направлении
оси x > 0,
а справа налево – в направлении оси x
< 0. Эти молекулы
находятся в слоях толщиной
 прилегающих к двум противоположным
сторонам площадки. Поэтому число таких
переходов будет равно соответственно
прилегающих к двум противоположным
сторонам площадки. Поэтому число таких
переходов будет равно соответственно
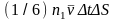 и
и
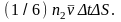 Множитель
Множитель
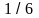 учитывает то обстоятельство, что в
каждом направлении оси X
движется
всех молекул. Величина переносимой ими
массы можно найти, умножив число
соответствующих переходов на массу
молекулы m.
Разность этих величин и даст результирующий
перенос массы через площадку
за время
:
учитывает то обстоятельство, что в
каждом направлении оси X
движется
всех молекул. Величина переносимой ими
массы можно найти, умножив число
соответствующих переходов на массу
молекулы m.
Разность этих величин и даст результирующий
перенос массы через площадку
за время
:
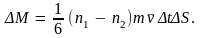 Плотность потока массы составит
Плотность потока массы составит
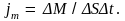 Следовательно,
Следовательно,
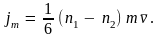
Вследствие малости можно записать
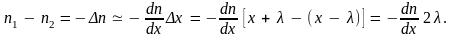
С учетом этого находим
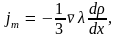
так как плотность
газа
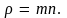 Тем самым мы пришли к закону Фика, и,
следовательно, коэффициент диффузии
Тем самым мы пришли к закону Фика, и,
следовательно, коэффициент диффузии
|
(4.4) |
4.4. Теплопроводность газов
Если температура газа в разных местах различна, то будет различной и средняя кинетическая энергия его молекул. Перемещаясь вследствие теплового движения из одних мест в другие и сталкиваясь друг с другом, молекулы переносят запасенную ими энергию. Происходит процесс выравнивания средних кинетических энергий молекул в разных местах, т.е. выравнивание температур. В этом и заключается явление теплопроводности.
Перенос энергии в форме теплоты подчиняется закону Фурье:
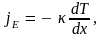
где
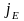 – плотность потока
тепла – величина, численно равная
энергии, переносимой в форме теплоты в
единицу времени через единичную площадку,
перпендикулярную оси x;
– плотность потока
тепла – величина, численно равная
энергии, переносимой в форме теплоты в
единицу времени через единичную площадку,
перпендикулярную оси x;
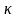 –
теплопроводность (коэффициент
теплопроводности);
–
теплопроводность (коэффициент
теплопроводности);
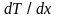 – градиент температуры, равный скорости
(быстроте) изменения температуры в
направлении оси X.
Знак минус показывает, что при
теплопроводности энергия переносится
в направлении убывания температуры.
– градиент температуры, равный скорости
(быстроте) изменения температуры в
направлении оси X.
Знак минус показывает, что при
теплопроводности энергия переносится
в направлении убывания температуры.
Расчет коэффициента
теплопроводности можно провести
аналогично расчету коэффициента
диффузии. Следует только при этом
заменить массу молекулы m
на среднюю кинетическую энергию
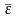 и считать ее различной в слоях 1 и 2. Тогда
для переносимой полной энергии через
площадку
за время
будем иметь
и считать ее различной в слоях 1 и 2. Тогда
для переносимой полной энергии через
площадку
за время
будем иметь
 =
=
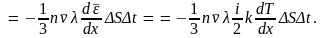
При получении
конечного выражения было учтено, что
средняя кинетическая энергия молекулы
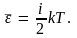 Преобразуем выражение, стоящее перед
градиентом температуры:
Преобразуем выражение, стоящее перед
градиентом температуры:

где
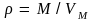 – плотность газа, M
– молярная масса газа, VM
– молярный объем,
– плотность газа, M
– молярная масса газа, VM
– молярный объем,
 – величина, называемая удельной
теплоемкостью газа при постоянном
объеме. С учетом этого получаем выражение
для плотности потока энергии:
– величина, называемая удельной
теплоемкостью газа при постоянном
объеме. С учетом этого получаем выражение
для плотности потока энергии:
.
Мы пришли к формуле, выражающей закон Фурье. Следовательно, коэффициент теплопроводности
|
(4.5) |