
– интеграл по состояниям, называемый статистическим интегралом (или статистической суммой); интегрирование проводится по всем состояниям с энергией из интервала от E до E + dE.
Распределения, определяемые выражениями (3.26) и (3.27) называют распределениями Гиббса соответственно в случае дискретного и непрерывного спектра энергии.
Глава 4
ЯВЛЕНИЯ ПЕРЕНОСА В ГАЗАХ
4.1. Средняя длина свободного пробега молекул газа
Участвуя в
тепловом движении, молекулы газа
непрерывно сталкиваются друг с другом.
Среднее расстояние
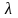 ,
проходимое молекулой между двумя
последовательными столкновениями,
называют средней длиной свободного
пробега, а соответствующий промежуток
времени
,
проходимое молекулой между двумя
последовательными столкновениями,
называют средней длиной свободного
пробега, а соответствующий промежуток
времени
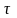 – средним временем свободного пробега.
Очевидно, что
– средним временем свободного пробега.
Очевидно, что
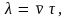 где
где
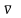 –
средняя (арифметическая) скорость
теплового движения молекул.
–
средняя (арифметическая) скорость
теплового движения молекул.
Будем считать,
что молекула А
движется относительно неподвижной
молекулы В
со средней относительной скоростью
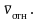 Введем параметр столкновения
Введем параметр столкновения
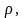 называемый прицельным расстоянием,
определив его как расстояние между
центром одной молекулы (А)
и линией первоначального движения
другой молекулы (В).
Столкновение между этими молекулами
произойдет, если прицельное расстояние
называемый прицельным расстоянием,
определив его как расстояние между
центром одной молекулы (А)
и линией первоначального движения
другой молекулы (В).
Столкновение между этими молекулами
произойдет, если прицельное расстояние
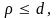 где
где
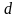 –
диаметр молекулы, т.е. если центр молекулы
В окажется
внутри диска площадью
–
диаметр молекулы, т.е. если центр молекулы
В окажется
внутри диска площадью
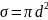 с центром, совпадающим с центром молекулы
А. Эту
площадь называют эффективным сечением
столкновения молекул; 𝜌
называют также эффективным радиусом
взаимодействия. За время t
с молекулой А
столкнутся все те молекулы, которые
попадут в объем круглого цилиндра с
осью, направленной вдоль вектора скорости
vотн,
площадью основания
с центром, совпадающим с центром молекулы
А. Эту
площадь называют эффективным сечением
столкновения молекул; 𝜌
называют также эффективным радиусом
взаимодействия. За время t
с молекулой А
столкнутся все те молекулы, которые
попадут в объем круглого цилиндра с
осью, направленной вдоль вектора скорости
vотн,
площадью основания
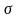 и высотой
и высотой
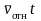 (рис. 4.1, а).
Число столкновений за время t
будет равно числу молекул в указанном
объеме, т.е. равно
(рис. 4.1, а).
Число столкновений за время t
будет равно числу молекул в указанном
объеме, т.е. равно
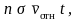 где n
– число молекул
в единице объема газа. За время
где n
– число молекул
в единице объема газа. За время
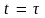 в
среднем произойдет только одно
столкновение, так что
в
среднем произойдет только одно
столкновение, так что
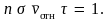 Откуда
Откуда
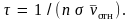
Для определения
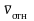 предположим, что до столкновения молекулы
имели скорости v1
и v2.
Тогда вектор относительной скорости
vотн
= v1
– v2.
Из треугольника скоростей (рис. 4.1, б)
по теореме косинусов имеем
предположим, что до столкновения молекулы
имели скорости v1
и v2.
Тогда вектор относительной скорости
vотн
= v1
– v2.
Из треугольника скоростей (рис. 4.1, б)
по теореме косинусов имеем
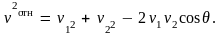 Среднее значение квадратов скоростей
всех молекул вследствие хаотичности
теплового движения одинаково:
Среднее значение квадратов скоростей
всех молекул вследствие хаотичности
теплового движения одинаково:
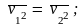 обозначим эту величину
обозначим эту величину
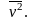 Кроме того, так как все направления
движения молекул равновероятны, то
косинус угла
Кроме того, так как все направления
движения молекул равновероятны, то
косинус угла
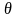 между векторами v1
и v2
после каждого столкновения одинаковое
число раз может принимать равные по
модулю положительные и отрицательные
значения, поэтому среднее значение
косинуса
между векторами v1
и v2
после каждого столкновения одинаковое
число раз может принимать равные по
модулю положительные и отрицательные
значения, поэтому среднее значение
косинуса
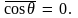 Тогда, усредняя значение квадрата
относительной скорости, будем иметь
Тогда, усредняя значение квадрата
относительной скорости, будем иметь
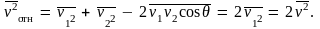
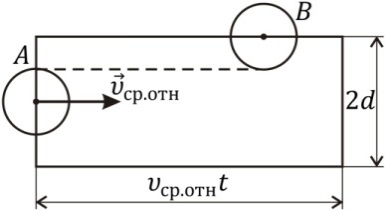
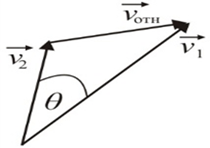
а) б)
Рис. 4.1
Поскольку, как
отмечалось в п. 3.6, средняя арифметическая
и
средняя квадратичная
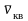 скорости пропорциональны друг другу,
то из этого равенства находим, что
скорости пропорциональны друг другу,
то из этого равенства находим, что
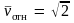
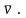 Подставляя это в
выражение для τ, получим
среднее время свободного пробега
молекулы
Подставляя это в
выражение для τ, получим
среднее время свободного пробега
молекулы
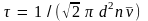 (4.1)
(4.1)
и среднее расстояние свободного пробега
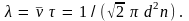 (4.2)
(4.2)
Среднее число столкновений молекул за единицу времени
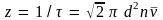 (4.3)
(4.3)
как и должно быть, чем больше размеры молекул и чем больше их концентрация, тем чаще сталкиваются молекулы друг с другом.
Газ можно считать
разреженным, а значит, и идеальным, если
средняя длина свободного пробега
молекулы много больше диаметра молекулы:
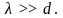 Подставляя сюда выражение (4.2), придем
к тому же критерию идеальности газа
(2.1).
Подставляя сюда выражение (4.2), придем
к тому же критерию идеальности газа
(2.1).
