3.3. Средняя энергия квантового гармонического

осциллятора

Применяя формулу (3.10), найдем среднюю тепловую энергию квантового гармонического осциллятора, находящегося при температуре T. Энергия такого осциллятора, как уже отмечалось выше, может принимать только дискретные значения

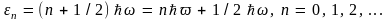
При определении средней тепловой энергии осциллятора его нулевую энергию 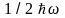можно не учитывать, т.е. принять ее за начало отсчета энергии осциллятора. Тогда 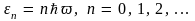Учитывая также, что кратность вырождения уровней энергии осциллятора 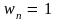при любом n, а

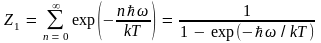
как сумма членов бесконечно убывающей геометрической прогрессии с первым членом, равным единице, и знаменателем 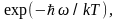получим

=

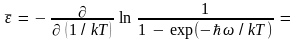
Проведя дифференцирование, для средней энергии гармонического осциллятора будем иметь

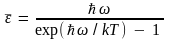. (3.11)

Формула (3.11) впервые была получена М. Планком и явилась первой формулой квантовой механики. Эта формула и определяет энергию, приходящуюся на каждую колебательную степень свободы. Полученное выражение существенно отличается от классического 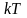и зависит от частоты колебания. Эта зависимость показана на рис. 3.2. Как видим, энергия убывает с ростом частоты 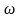от значения = (при ) до нуля (при ). Классическое значение 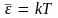осциллятор имеет при низких частотах и высоких температурах, когда В этом случае экспоненту можно разложить в ряд по степеням величины 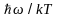и ограничиться первыми двумя членами. Тогда получим

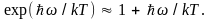
Подставляя это в формулу (3.9), придем к классическому значению .

Поскольку величина 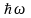представляет собой расстояние между соседними уровнями энергии осциллятора, то условие совпадает с общим условием (3.1) пренебрежения квантованием энергии. При выполнении этого условия квантовый характер осциллятора не проявляется, и он ведет себя как классическая колеблющаяся частица, обладающая средней тепловой энергией

3.4. Распределение частиц по энергии в случае

непрерывного спектра

Рассмотрим теперь случай, когда энергия частицы может принимать любые непрерывные значения. Это имеет место, например, в случае поступательного движения молекул газа или когда, в соответствии с (3.1), расстояние между уровнями энергии частицы мало по сравнению с ее средней тепловой энергией. В этом случае определяют вероятность того, что частица обладает каким-либо значением энергии в интервале от до 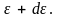В этом квазиклассическом случае величина заменяется на кинетическую энергию частицы, а кратность вырождения уровня - на число состояний dw(ε), соответствующих интервалу энергий от до Учитывая, что это число состояний dw(ε) ~ 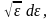будем иметь

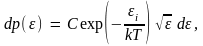
где C – постоянный коэффициент пропорциональности. Введем функцию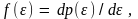 определяющую плотность вероятности обнаружить частицу в состоянии с каким-либо значением энергии в интервале от до Тогда

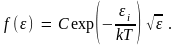
Постоянная С определяется условием нормировки

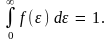
Поскольку

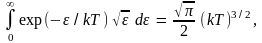
будем иметь

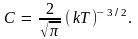
Тогда искомая вероятность того, что частица обладает каким-либо значением энергии в интервале от до определится как

(3.12)

а плотность этой вероятности

(3.13)

Умножив вероятность (3.12) на число молекул газа N, можно определить число молекул, обладающих энергией, заключенной в интервале от до

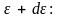
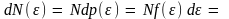
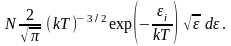= (3.14)

Соотношение (3.14) называют распределением Максвелла –Больцмана по кинетической энергии частиц, а функцию 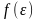– функцией распределения Максвелла – Больцмана по кинетической энергии частиц График этой функции для двух значений температур T₁ и 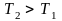показан на рис. 3.3. Наличие двух конкурирующих множителей – монотонно возрастающего и монотонно убывающего – обусловливает существование у функции максимума при некотором значении ε = ε_в. Этой энергией обладает наибольшее число молекул газа, поэтому ее называют наиболее вероятной кинетической энергией. Ее можно найти из условия максимума функции 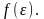Получим 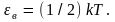Видим, что с увеличением температуры эта наиболее вероятная кинетическая энергия возрастает, а максимум кривой распределения смещается в сторону больших энергий. Молекулам становятся доступными большие значения кинетической энергии. Из рис. 3.3. видно, что кривая , соответствующая более высокой температуре T₂, в области малых значений энергии лежит ниже той же кривой, соответствующей более низкой температуре 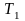, а в области больших значений энергии – выше. Это означает, что с повышением температуры газа вероятность обнаружить молекулу с большим значением кинетической энергии становится больше вероятности обнаружить молекулу с малым значением кинетической энергии. Число молекул с малым значением кинетической энергии уменьшается, а число молекул с большим значением кинетической энергии возрастает. Происходит перераспределение молекул по энергиям. В этом и состоит процесс нагревания газа.

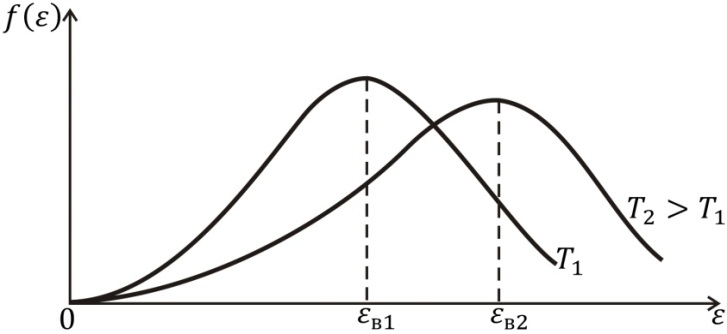
Рис. 3.3

Площадь под кривой от температуры не зависит и в соответствии с условием нормировки функции равна единице.

Зная функцию распределения можно найти среднее значение кинетической энергии. Как легко убедиться,

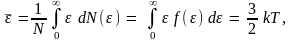
что совпадает с ранее полученным значением. Так и должно быть, ибо выбор β в виде определялся именно этим обстоятельством.