
Вопросы и упражнения
1. Даны три вектора e1(1,2), e2(–3,1), e3(–3,–2). Найти координаты вектора 2e1 + e2 – 3e3.
Ответ: 1) (8,11);
2.
Даны три вектора e1(1,1),
e2(2,–1),
e3(–4,–1).
Найти числа
 такие, что
такие, что
 .
.
Ответ:
1)
 ,
,
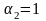 .
.
3. Проверить, что векторы e1(1,2), e2(–3,1) образуют базис на плоскости. Найти координаты вектора e3(–2, 3) в этом базисе.
Ответ: 1) (1,1);
4. Даны три вектора e1(1,2,1), e2(–3,1,0), e3(–3,–2,–1). Найти координаты вектора 2e1 + e2 – 2e3.
Ответ: 1) (5,9,4);
5.
Даны четыре вектора e1(1,1,1),
e2(2,–1,1),
e3(–4,–1,1),
e4(0,0,4).
Найти числа


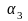 такие, что
такие, что
 .
.
Ответ:
1)
,
,
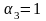 .
.
6. Даны три вектора e1(1,1), e2(–3,1), e3(–1,1). Образуют ли эти векторы базис?
Ответ: 1) нет, так как любые три вектора на плоскости линейно зависимы; 2) да, так как векторы неколлинеарны; 3) да, так как любой другой вектор на плоскости можно разложить по этим векторам; 4) нет, так как существуют векторы, которые нельзя разложить по данным векторам.
7. Даны четыре вектора e1(1,1,1), e2(–3,1,0), e3(–1,0,0), e4(0,1,1). Образуют ли эти векторы базис?
Ответ: 1) нет, так как любые четыре вектора в пространстве линейно зависимы; 2) да, так как векторы некомпланарны; 3) да, так как любой другой вектор в пространстве можно разложить по этим векторам; 4) нет, так как существуют векторы, которые нельзя разложить по данным векторам.
3.6. Ранг матрицы
Пусть
 — произвольная i-я
строка матрицы
— произвольная i-я
строка матрицы
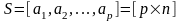 .
Каждая строка является элементом линеала
,
поэтому если число строк в матрице
.
Каждая строка является элементом линеала
,
поэтому если число строк в матрице
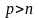 ,
то строки
,
то строки
 линейно зависимы. С другой стороны,
очевидно, что среди
существует ровно
линейно зависимы. С другой стороны,
очевидно, что среди
существует ровно
 строк, являющихся линейно независимыми,
по которым можно разложить остальные
(n – k)
строк.
строк, являющихся линейно независимыми,
по которым можно разложить остальные
(n – k)
строк.
Определение 3.6.1. Указанная совокупность k строк называется строчечным базисом, а число k — строчечным рангом матрицы.
Если
матрица
 ,
где
,
где
 ,
то в ней существует не более p
линейно
независимых столбцов. Среди столбцов
,
то в ней существует не более p
линейно
независимых столбцов. Среди столбцов
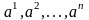 имеется ровно
имеется ровно
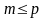 линейно независимых, по которым можно
разложить любой из остальных
линейно независимых, по которым можно
разложить любой из остальных
 столбцов.
столбцов.
Определение 3.6.2. Указанная совокупность m столбцов называется столбцовым базисом, а число m — столбцовым рангом матрицы S.
Теорема 3.6.1. Строчечный (столбцовый) ранг любой матрицы не зависит от выбора строчечного (столбцового) базиса.
Доказательство.
Проведем доказательство для строчечного
базиса. Пусть
 и
и
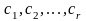 два разных строчечных базиса одной и
той же матрицы. Предположим, что
два разных строчечных базиса одной и
той же матрицы. Предположим, что
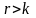 .
Поскольку
базис, то строки
.
Поскольку
базис, то строки
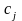 ,
,
 можно разложить по этому базису, т. е.
можно разложить по этому базису, т. е.
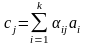 ,
.
Так как
линейно независимы, то в соответствии
с теоремой 3.5.3 строки
линейно зависимы. Полученное противоречие
доказывает, что
,
.
Так как
линейно независимы, то в соответствии
с теоремой 3.5.3 строки
линейно зависимы. Полученное противоречие
доказывает, что
 .
Аналогично показывается, что k
не может
быть больше
r,
поэтому
.
Аналогично показывается, что k
не может
быть больше
r,
поэтому
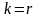 .
.
Пусть
дана прямоугольная матрица
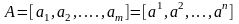 ,
,
 .
Допустим, что строчечный ранг этой
матрицы равен k.
Без ограничения общности можно считать,
что первые k
строк образуют базис, а любая другая
строка матрицы A
представима в виде их линейной комбинации,
т. е.
.
Допустим, что строчечный ранг этой
матрицы равен k.
Без ограничения общности можно считать,
что первые k
строк образуют базис, а любая другая
строка матрицы A
представима в виде их линейной комбинации,
т. е.
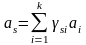 ,
,
 . (3.6.1)
. (3.6.1)
Из
первых k
строк матрицы A
построим
вспомогательную матрицу
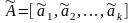 ,
где
,
где
 ,
,
 .
Пусть
.
Пусть
 — j-й
столбец матрицы
— j-й
столбец матрицы
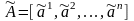 .
.
Лемма 3.6.1. Если
для некоторых чисел
 справедливо
равенство
справедливо
равенство
 ,
то
,
то
 .
.
Доказательство.
Пусть
 ,
тогда произведение
,
тогда произведение
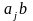 определяет j-ю
компоненту столбца
определяет j-ю
компоненту столбца
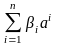 .
Из равенства
следует, что первые k
компонент
указанного столбца
по построению матрицы
.
Из равенства
следует, что первые k
компонент
указанного столбца
по построению матрицы
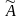 равны нулю, т. е.
равны нулю, т. е.
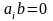 ,
.
Тогда для любого
в силу (3.6.1) имеем
,
.
Тогда для любого
в силу (3.6.1) имеем
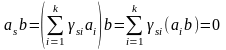 .
.
Теорема 3.6.2. Строчечный ранг любой матрицы равен ее столбцовому рангу.
Доказательство.
Допустим, что столбцовый базис матрицы
состоит из
 первых столбцов
первых столбцов
 .
Так как
.
Так как
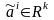 ,
то
,
то
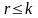 .
Столбцы
образуют базис, поэтому для любого
.
Столбцы
образуют базис, поэтому для любого
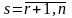 имеем
имеем
 .
Следовательно, справедливо равенство
.
Следовательно, справедливо равенство
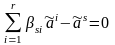 .
Тогда в силу леммы 3.6.1 имеем
.
Тогда в силу леммы 3.6.1 имеем
 ,
отсюда следует, что
,
отсюда следует, что
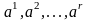 есть столбцовый базис матрицы A.
Поскольку имеем неравенство
,
то столбцовый ранг не превосходит
строчечный. Аналогичные рассуждения
относительно строчечного базиса приводят
к выводу, что
есть столбцовый базис матрицы A.
Поскольку имеем неравенство
,
то столбцовый ранг не превосходит
строчечный. Аналогичные рассуждения
относительно строчечного базиса приводят
к выводу, что
 .
Следовательно, строчечный ранг матрицы
совпадает со столбцовым рангом.
.
Следовательно, строчечный ранг матрицы
совпадает со столбцовым рангом.
Определение
3.6.3. Общее
значение столбцового и строчечного
ранга называется рангом
матрицы А
и обозначается
 .
.
Теорема 3.6.3.
Определитель
матрицы
 равен нулю тогда и только тогда, когда
равен нулю тогда и только тогда, когда
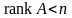 .
.
Доказательство.
Достаточность.
Пусть
,
следовательно, строки матрицы A
линейно
зависимы. Поэтому в соответствии с
теоремой 3.3.1, по крайней мере, одну из
них можно разложить по оставшимся
строкам. Без ограничения общности будем
считать, что
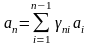 .
Определитель
.
Определитель
 не изменяется, если к любой из его строк
прибавить другую строку, умноженную на
заданное число. Следовательно,
не изменяется, если к любой из его строк
прибавить другую строку, умноженную на
заданное число. Следовательно,

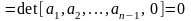 .
.
Необходимость.
Доказательство
проведем методом математической индукции
по числу n.
При
 имеем
имеем
 ,
т. е.
,
т. е.
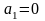 — линейно зависимая строка. Допустим,
что теорема доказана для
— линейно зависимая строка. Допустим,
что теорема доказана для
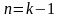 ,
докажем ее для случая
,
докажем ее для случая
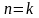 .
.
Пусть
 .
Построим вспомогательные строки, считая
.
Построим вспомогательные строки, считая
 :
:
 ,
…,
,
…,
 .
.
Тогда
 ,
,
следовательно,
 .
.
По
индукционному предположению
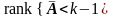 ,
т. е. строки
,
т. е. строки
 ,
…,
,
…,
 линейно зависимы. Но тогда линейно
зависимыми являются
линейно зависимы. Но тогда линейно
зависимыми являются
 ,
следовательно, существуют числа
,
следовательно, существуют числа
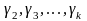 не равные нулю одновременно, что
не равные нулю одновременно, что
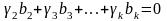 .
Поэтому справедливо соотношение
.
Поэтому справедливо соотношение
 ,
,
отсюда
следует линейная зависимость строк
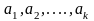 ,
т. е.
,
т. е.
 .
.
Теорема 3.6.4. Ранг матрицы равен наибольшему порядку миноров, отличных от нуля.
Доказательство.
Допустим, что
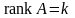 .
Тогда в матрице A
существует ровно k
линейно независимых строк, образующих
строчечный базис, и k
линейно
независимых столбцов, составляющих
столбцовый базис. Поэтому минор k-го
порядка, построенный на указанных
строках и столбцах, очевидно, не равен
нулю. При этом все миноры порядка k + 1
и выше (если таковые имеются) будут равны
нулю, как содержащие линейно зависимые
строки и линейно зависимые столбцы.
.
Тогда в матрице A
существует ровно k
линейно независимых строк, образующих
строчечный базис, и k
линейно
независимых столбцов, составляющих
столбцовый базис. Поэтому минор k-го
порядка, построенный на указанных
строках и столбцах, очевидно, не равен
нулю. При этом все миноры порядка k + 1
и выше (если таковые имеются) будут равны
нулю, как содержащие линейно зависимые
строки и линейно зависимые столбцы.
Лемма 3.6.2. Ранг произведения двух матриц не превосходит ранг каждого из сомножителей.
Доказательство. Пусть
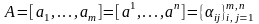 ,
,
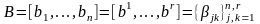 .
.
Произведение
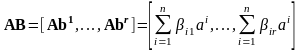 ,
,
следовательно,
каждый столбец произведения есть
линейная комбинация столбцов матрицы
A,
поэтому
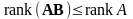 .
Аналогично, имеем
.
Аналогично, имеем
 ,
,
отсюда
каждая строка произведения равна
линейной комбинации строк матрицы
 ,
т. е.
,
т. е.
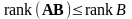 .
.
Лемма 3.6.3. Для
произвольной невырожденной матрицы
и любой
матрицы A
справедливо равенство
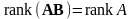 .
.
Доказательство.
Если матрица
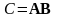 ,
то в силу леммы 3.6.2
,
то в силу леммы 3.6.2
 .
Так как матрица
по условию является невырожденной, то
существует обратная матрица
.
Так как матрица
по условию является невырожденной, то
существует обратная матрица
 .
Умножим матрицу C
справа на
,
получаем
.
Умножим матрицу C
справа на
,
получаем
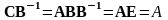 ,
следовательно,
,
следовательно,
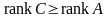 .
Таким образом, справедливо равенство
.
Таким образом, справедливо равенство
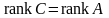 .
.
