Глава 3. Линейные пространства

3.5. Базис и размерность линеала

Определение 3.5.1. Упорядоченная совокупность линейно независимых векторов e₁, e₂, …, e_n линеала L называется базисом линеала, если для каждого вектора x  L найдутся вещественные числа _i, i = 1, 2,…, n, что

x =  .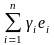

Последнее равенство называют разложением вектора x по базису e₁, e₂, …, e_n.

На основании данного определения можно утверждать, что в векторном пространстве V ¹ произвольный ненулевой вектор может быть взят в качестве базисного, в пространстве V ² упорядоченная пара неколлинеарных векторов образует базис, а в V ³ упорядоченная тройка некомпланарных векторов образует базис.

В пространстве R ⁿ векторы u₁ = (1, 0,…, 0), u₂ = (0, 1,…, 0),…, u_n = (0, 0,…, 0, 1) образуют базис, поскольку они линейно независимы и любой вектор x = (₁, ₂,…, _n)  R ⁿ представим в виде .

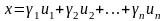Отметим, что в определении базиса порядок элементов существенен, так как, переставляя элементы базиса, получаем снова базис, но уже другой.

Определение 3.5.2. Числа ₁, ₂,…, _n, фигурирующие в разложении элемента x линеала L по заданному базису e₁, e₂, …, e_n называются координатами данного вектора относительно рассматриваемого базиса.

Теорема 3.5.1. Координаты всякого элемента линеала L относительно заданного базиса определяются однозначно.

Доказательство. Допустим, что e₁, e₂, …, e_n — базис линеала L. Пусть для некоторого вектора x наряду с разложением x = существует еще и другое разложение x =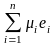 . Но тогда справедливо равенство 0 = . Базисные элементы e₁, e₂, …, e_n линейно независимы, поэтому для всех i = 1, 2, …, n имеем _i = _i.

Теорема 3.5.2. При сложении элементов линеала L их координаты складываются, а при умножении вектора на вещественное число все его координаты умножаются на данное число.

Доказательство. Пусть элементы e₁, e₂, …, e_n образуют базис в L, x и y — произвольные элементы из L, λ — произвольное вещественное число, s = x + y, p = x.

Ясно, что x = , y = , s =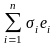 , p =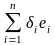 . Используя аксиомы 1^ — 8^ линеала L, получаем

s = x + y = + = ,

p = x = λ( ) = .

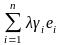В силу единственности разложения по базису имеем _i = _i + _i , _i = _i, i = 1, 2,…, n.

Теорема 3.5.3. Если каждый из (n + 1) элементов y₀, y₁,…, y_n линеала L представим в виде линейной комбинации n линейно независимых элементов x₁, x₂,…, x_n того же линеала, т. е.

y_i = 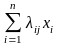 , ,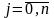 (3.5.1)

то элементы y₀, y₁,…, y_n линейно зависимы.

Доказательство см., например, учебник Кузютин В.Ф., Зенкевич Н.А., Еремеев В.В. «Геометрия».

Следствие 3.5.1. Любые (n + 1) векторов линейного пространства 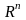являются линейно зависимыми.

Доказательство. Возьмем произвольно векторы y_k = (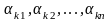 ), 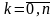. Поскольку u₁ = (1, 0,…, 0), u₂ = (0, 1,…, 0),…, u_n = (0, 0,…, 0, 1) образуют базис в пространстве , то для любого имеем y_k =  . Следовательно, в силу теоремы 3.5.3 произвольные (n + 1) векторов из линеала линейно зависимы.

Следствие 3.5.2. Любые два базиса линеала L содержат одно и то же число векторов.

Доказательство. Пусть e₁, e₂, …, e_n базис линеала L, а 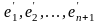другой базис этого же линеала. Так как 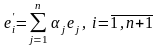, причем e₁, e₂, …, e_n линейно независимы. В силу теоремы 3.5.3 — линейно зависимы. Полученное противоречие и доказывает следствие.

Определение 3.5.3. Линеал L называют n-мерным, если в нем существует базис, состоящий из n векторов.

Число n называют размерностью линеала L и обозначают dim(L) = n.

Таким образом, размерность пространства — это наибольшее число его линейно независимых элементов.

Если линеал L является n-мерным и необходимо подчеркнуть его размерность, то обычно используют обозначение 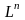. Ясно, что dim(V ¹) = 1 dim(V ²) = 2, dim(V ³) = 3.

Линеал , содержащий единственный нулевой элемент, является нуль–мерным.

Определение 3.5.4. Линеал L называется бесконечномерным, если для любого натурального числа N в нем найдется линейно независимая система, состоящая из N элементов.

Примером бесконечномерного линеала является линейное пространство непрерывных на заданном отрезке функций.

Теорема 3.5.4. Для того чтобы линеал L был n-мерным, необходимо и достаточно, чтобы в нем существовала линейно независимая система, состоящая из n элементов, а всякая система, содержащая более n векторов, была бы линейно зависимой.

Доказательство. Необходимость. Если линеал является n –мерным, то в нем существует базис e₁, e₂,…, e_n, состоящий из n элементов. Произвольный вектор x_j  L, представим в виде линейной комбинации векторов e₁, e₂,…, e_n, поэтому любая совокупность более чем n элементов является линейно зависимой.

Достаточность. Пусть e₁, e₂,…, e_n линейно независимые элементы. Возьмем произвольный вектор x  L. По условию векторы e₁, e₂,…, e_n, x линейно зависимы, т. е. существует нетривиальная линейная комбинация α₁e₁ + α₂e₂ +…+ α_ne_n + αx = 0, причем α  0. Но тогда x может быть разложен по e₁, e₂,…, e_n, т. е. эти элементы — базис линеала L.

В n-мерном линеале L всякий базис состоит из n упорядоченных линейно независимых элементов, при этом любой вектор линеала L_n единственным образом представим в виде линейной комбинации базисных элементов.

Это утверждение не вытекает из аксиом 1^° – 8^° линейного пространства. Поэтому следует сформулировать новую аксиому.

9^°. (аксиома размерности). Линейное пространство L конечномерно и его размерность равна n.

При выполнении этой аксиомы из аксиом 1^° – 8^° очевидно вытекает сформулированное утверждение.