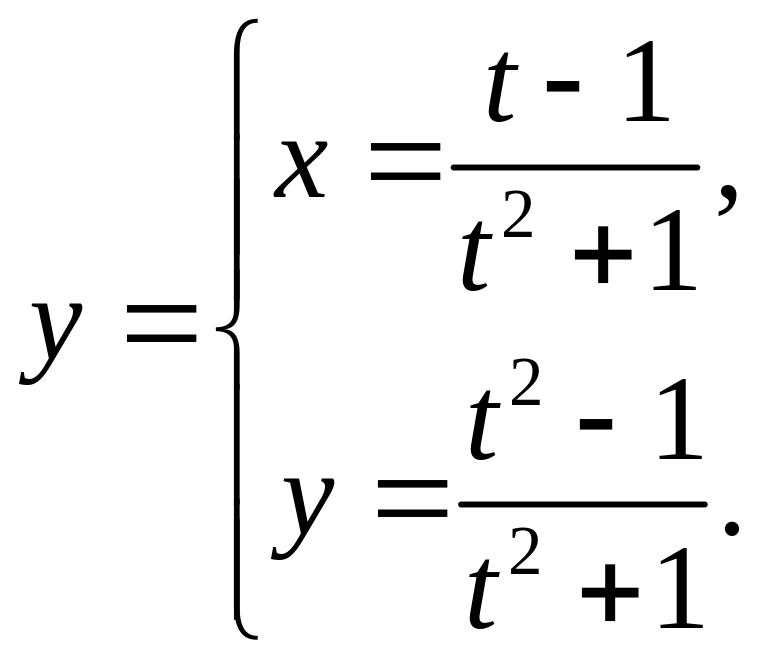9. Материально-техническое обеспечение дисциплины:

Специально оборудованные кабинеты и аудитории: компьютерные классы, аудитории, оборудованные мультимедийными средствами обучения.

10. Методические рекомендации по организации изучения дисциплины.

Контроль знаний студентов включает формы текущего и итогового контроля. Текущий контроль осуществляется в виде контрольной работы и домашнего задания. Итоговый контроль осуществляется в виде зачетной контрольной работы и письменного экзамена. Итоговая оценка О_итог по 10-балльной шкале формируется как взвешенная сумма О_итог=0,1*О_к.р.+0,1*О_д.з.+0,3*О_зач.+0,5*О_экз., округленная до целого числа баллов. О_к.р., О_д.з, О_зач. и О_экз. обозначают оценки по 10-балльной шкале за контрольную работу, домашнее задание, зачет и экзамен соответственно.

Таблица соответствия оценок по десятибалльной и системе зачет/незачет

Оценка по 10-балльной шкале	Оценка по 5-балльной шкале
1	незачет
2
3
4	зачет
5
6
7
8
9
10

Таблица соответствия оценок по десятибалльной и пятибалльной системе

По десятибалльной шкале	По пятибалльной системе
1 – неудовлетворительно 2 – очень плохо 3 – плохо	неудовлетворительно – 2
4 – удовлетворительно 5 – весьма удовлетворительно	удовлетворительно – 3
6 – хорошо 7 – очень хорошо	хорошо – 4
8 – почти отлично 9 – отлично 10 - блестяще	отлично - 5

Для оценки качества освоения дисциплины можно использовать задачи (более 4000 по всем разделам курса), приведенные в задачнике: Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1997.

Типовой вариант контрольной работы (1 модуль)

1. Исследуйте функцию 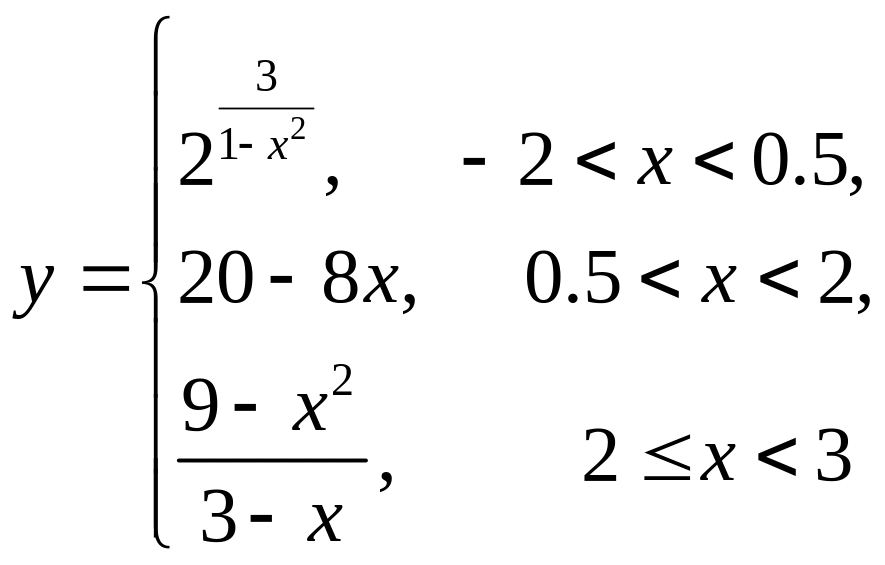на непрерывность, укажите характер точек разрыва функции и постройте эскиз ее графика.

Найдите пределы:	;	;
Найдите производную :	; ;

7. Укажите для функции 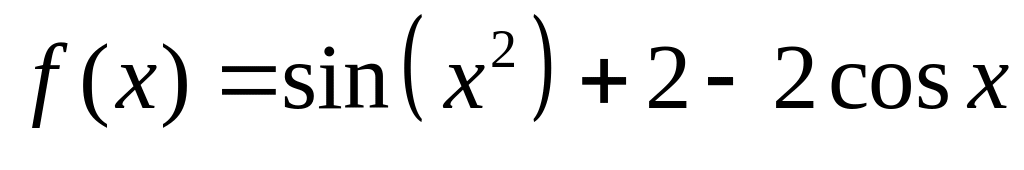эквивалентную функцию вида 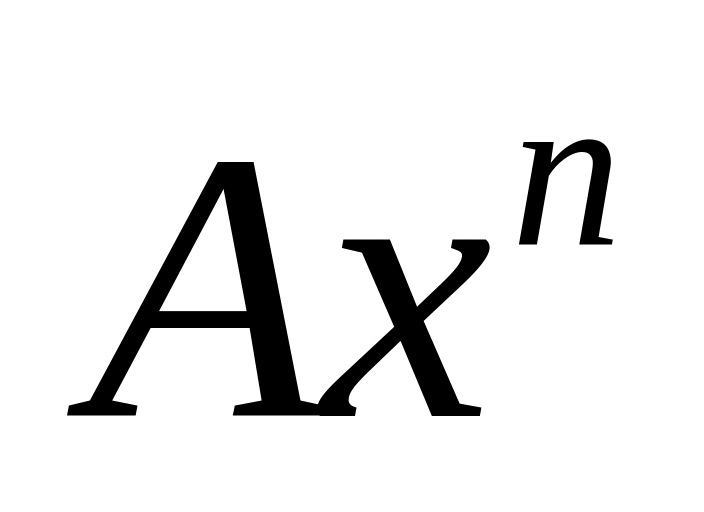при .

8. Найдите предел 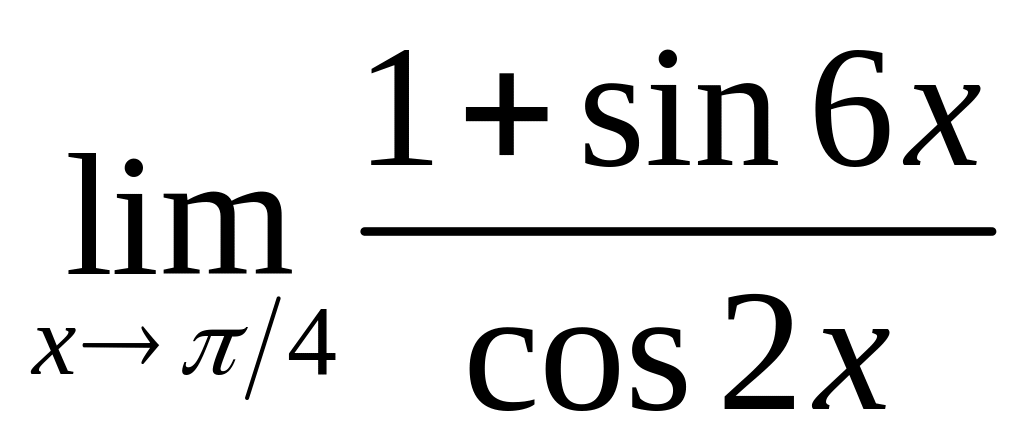, используя правило Лопиталя.

9. Найдите значения и 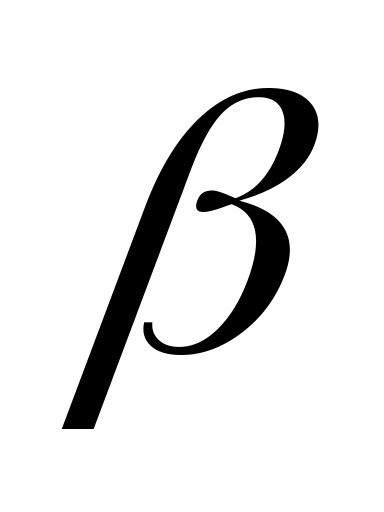, при которых функция является бесконечно малой при .

10. Если 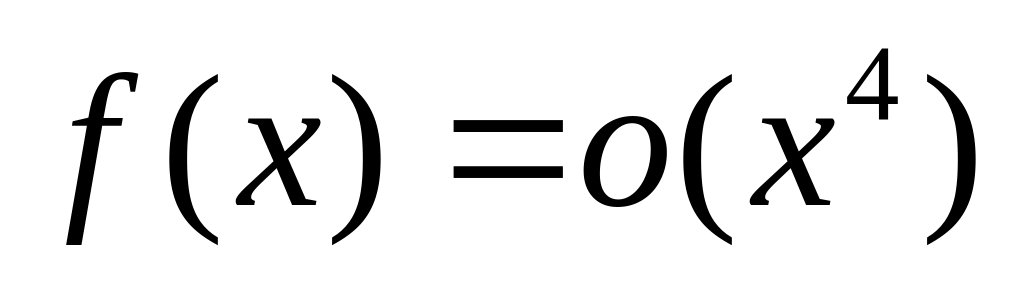при , то верно ли, что .

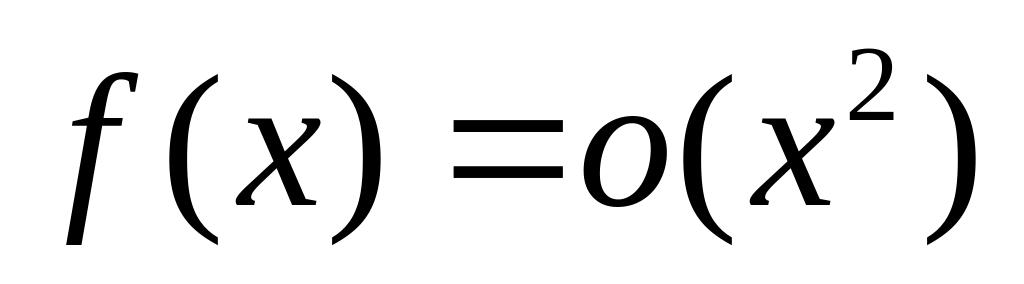Типовой вариант зачетной контрольной работы (2 модуль)

Основная часть

ЗАДАЧА 1. Найдите предел .

ЗАДАЧА 2. Докажите, используя определение предела функции в точке, что функция непрерывна в точке .

ЗАДАЧА 3. Укажите для функции эквивалентную функцию вида при .

ЗАДАЧА 4. Найдите производные и функции , заданной параметрически: .

ЗАДАЧА 5. Исследуйте на экстремум функцию .

ЗАДАЧА 6. Найдите экстремум функции при условии с помощью функции Лагранжа. Нарисуйте: а) график условия; б) изолинии, проходящие через стационарные точки функции Лагранжа; в) градиент в этих точках.

ЗАДАЧА 7. Спрос и предложение зависят от цены следующим образом: , . Найдите наибольшее значение дохода и определите эластичность функции дохода в точке максимума.