Практичне заняття №3 Множини. Операції над ними

Мета роботи: Ознайомлення студентів з основними поняттями теорії множин, проведенням операцій над множинами, доведення тотожностей в теорії множин різноманітними способами.

Теоретичні відомості

На підставі інтуїтивних уявлень про будь-які подібні чітко визначені сукупності об’єктів сформувалося математичне поняття множини як об’єднання об’єктів у єдине ціле. Саме такої точки зору дотримувався засновник теорії множин німецький математик Георг Кантор. Група математиків, які працювали під псевдонімом Н.Бурбаки, стверджувала: «Множина утворюється з елементів, що мають певні властивості і знаходяться у певних відношеннях між собою чи з елементами інших множин».

Для позначення конкретних множин використовують великі літери , , ,... або великі літери з індексами , і т. д. Для позначення елементів множин загалом застосовують малі літери , , , ... або малі літери з індексами , і т.д.

Для позначення того, що є елементом множини (тобто належить ), будемо застосовувати запис , а запис означатиме, що елемент не належить множині . Записом користуються як скороченням для запису . Символ називається символом належності.

Приклад 3.1. Наведемо ще кілька прикладів множин:

• Множина цифр десяткової системи. Позначимо її ;

• Множина цифр двійкової системи. Позначимо її ;

• Множина парних чисел. Позначимо її ;

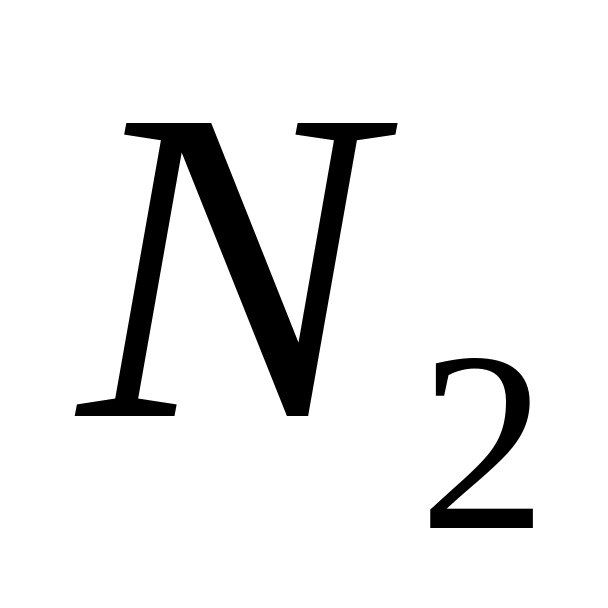• Множина видів навчальних занять студентів. Позначимо її .

Є кілька способів подання множин.

1. Вербальний (словесний) за допомогою опису властивостей, які повинні мати елементи множин.

2. Список (перелік) усіх елементів у фігурних дужках.

Приклад 3.2. Стосовно зазначених вище прикладів маємо:

• ;

• ;

• .

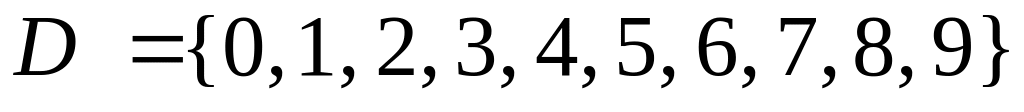• , де

– лекції;

– лабораторні роботи;

– практичні заняття;

– індивідуальна робота;

– самостійна робота.

3. Предикатний (висловлювальний, породжувальний) за допомогою предиката, тобто множина задається у вигляді або , де набуває значення «істина» для елементів множини.

Приклад 3.3. Приклади предикатів:

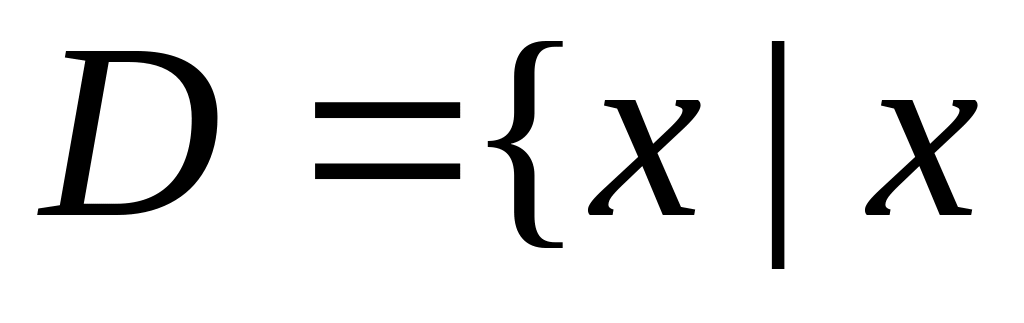• – цифра десяткової системи};

• – цифра двійкової системи ;

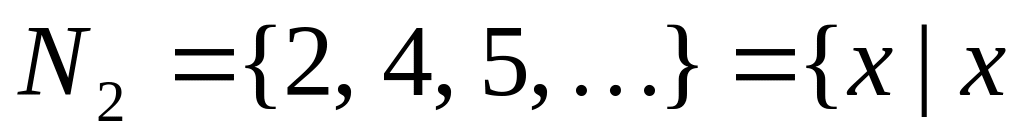• – парне число ;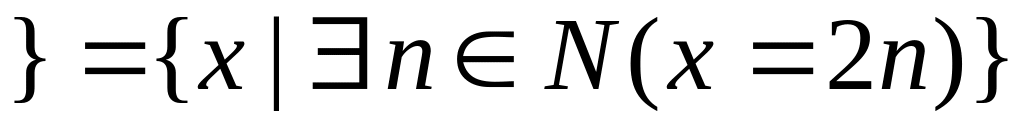

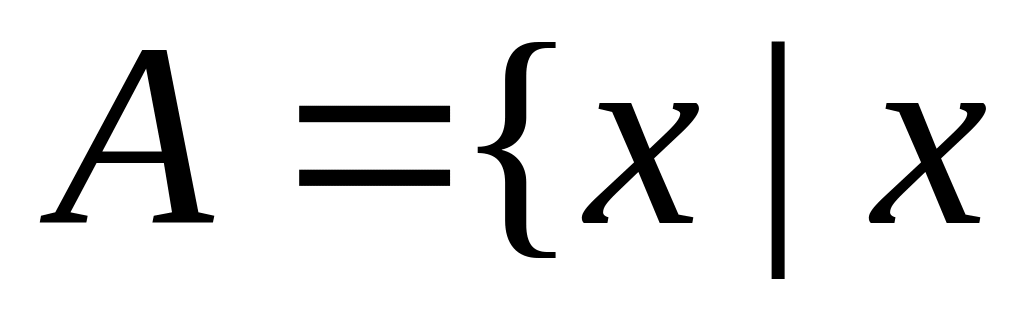• – від навчальних занять студентів}.

4. За допомогою породжувальної процедури, яка описує спосіб отримання елементів множини із вже існуючих або інших об’єктів, якщо такий спосіб існує. Елементами множини є всі об’єкти, які можуть бути створені за допомогою цієї процедури. Частіше за все породжуюча процедура задається рекурсивними правилами.

Приклад 3.4. Задамо породжуючі процедури для раніше наведених прикладів:

• для множини :

а) ; б) якщо , то теж , поки ;

• для множини B:

а) ; б) якщо , то теж , поки ;

• для множини :

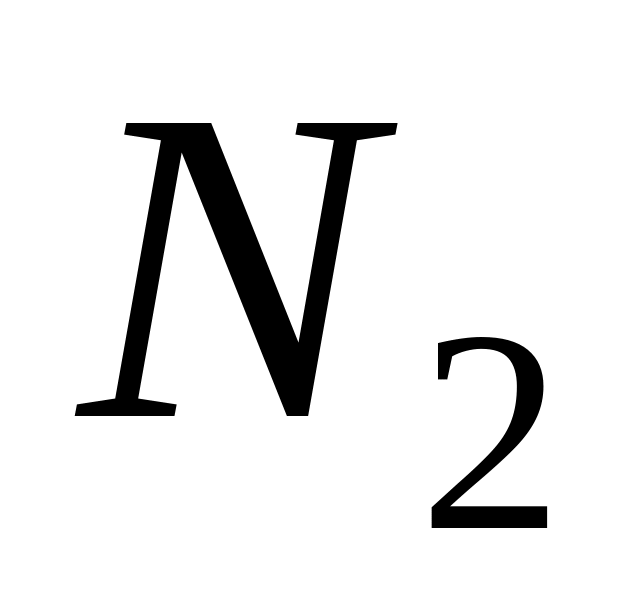а) ; б) якщо , то теж ;

• для множини породжуючої процедури не існує, тому що не зрозуміло яким чином можна отримати наступний елемент із вже існуючих.

5. Аналітичний (за допомогою формул).

У теорії множин використовується поняття порожньої множини. Позначається вона символом .

Множина може взагалі не містити елементів, наприклад

– непарне число, що ділиться на ;

.

Для позначення цього факту вводиться поняття порожньої множини.

Розглянемо дві множини А та В і введемо кілька операцій над ними. Для графічної ілюстрації будемо використовувати кола Ейлера. Для зображення множини на площині креслять замкнену лінію із заштрихованою внутрішньою областю (найчастіше – це коло, звідси й назва відповідного інструмента, що широко застосовується в теорії множин).

Об’єднання і ( ) – множина, що складається з усіх елементів множини , всіх елементів множини і не містить ніяких інших елементів (рис. 3.1), тобто ,

Рис. 3.1. Об’єднання множин

Переріз і – множина, що складається з тих і тільки тих елементів, які належать одночасно множині та множині (рис. 3.2), тобто ,

Рис. 3.2. Переріз множин

Різниця і (відносне доповнення) – множина, що складається з тих і тільки тих елементів, які належать множині й не належать (рис. 3.3), тобто .

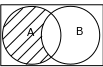
Рис. 3.3. Різниця множин

Диз’юнктивна сума і (симетрична різниця) – множина, що складається з усіх елементів , які не належать множині , й усіх елементів , які не належать множині , та яка не містить ніяких інших елементів (рис. 3.4), тобто .

Рис. 3.4. Диз’юнктивна сума множин

Очевидно, що .

Звичайно, вже в контексті деякої задачі, в якій виникає конкретна множина, явно або неявно обмежується сукупність об’єктів, що є допустимими (натуральні числа – серед цілих або дійсних залежно від контексту, студенти – серед студентів факультету, університету, або серед всіх студентів України, або світу залежно від контексту).

Зручно сукупність допустимих об’єктів зафіксувати явно, як деяку множину та вважати, що множини, які розглядаються, складаються з елементів цієї множини. Її називають основною множиною (універсумом) і позначають .

Множина називається підмножиною множини , якщо кожен елемент є елементом .

Для позначення цього факту вводиться знак « » – символ включення (або « »); іншими словами, .

Приклад 3.5. Нехай – людська істота} і – людська істота жіночої статі}; тоді зрозуміло, що .

Дві множини рівні, якщо вони складаються з одних і тих самих елементів:

.

Наприклад, .

Справджується таке твердження: тоді і тільки тоді, коли .

Можна довести таке твердження: включення множин транзитивне, тобто справджується така рівність: якщо , то .

Операції над множинами, як і операції над логічними змінними, мають деякі властивості. Останні виражаються сукупністю тотожностей незалежно від конкретного вмісту множин, що входять у них, і є підмножинами деякого універсуму . Ми вже знаємо, що множина об’єктів разом з операціями утворюють алгебру. Множина всіх множин разом з операціями об’єднання, перерізу і абсолютного доповнення утворюють алгебру, яка називається алгеброю множин. Її основні властивості або закони алгебри множин наведені нижче.

1. Комутативні закони

а) ;

б) .

2. Асоціативні закони

а) ;

б) .

3. Дистрибутивні закони

а) ;

б) .

Властивості  та

4 а) ;	4 б) .
5 а) ;	5 б) .
6 а) ;	6 б) .
7 а) ;	7 б) .

Закон ідемпотентності (самопоглинання)

8 а) ;

8 б) .

Закон поглинання

9 а) ;

9 б) .

Теорема де Моргана

10 а) ;

10 б) .

Властивості доповнення, різниці та рівності

11) ;	14) ;
12) ;	15) ;
13) ;	16) .

Основний метод доведення тотожності в алгебрі множин ґрунтується на застосуванні означення рівності множин і твердження про рівність множин. Такий зручний інструмент, як кола Ейлера може бути використаний для доведення тотожностей алгебри множин тільки після певної формалізації. Ми її не робитимемо, тому використовуватимемо кола Ейлера як ілюстративний інструмент.

Приклад 3.6. Спочатку доведемо тотожність 3а) , використовуючи твердження про рівність множин.

Доведемо, що . Для цього візьмемо будь-яке , тоді за означенням операцій « » і « », . За законом дистрибутивності диз’юнкції відносно кон’юнкції маємо, що , тобто або , що і було потрібно довести.

Доведемо, що . Для цього візьмемо будь-яке . Звідси або , тобто , що і було потрібно довести.

Згідно з твердженням про рівність множин 3а) .

Доведемо, що за означенням рівності множин. Для цього знову візьмемо будь-яке , тоді за означенням операцій « » і « », це еквівалентне тому, що . Це в свою чергу за законом дистрибутивності диз’юнкції відносно кон’юнкції еквівалентне тому, що , тобто або . Таким чином ми довели, що

тобто .

За означенням рівності двох множин це означає, що .

Доведемо ту саму тотожність алгебраїчним способом. Нагадаємо, що при цьому ми маємо використовувати основні властивості (тотожності) алгебри множин причому, якщо ми доводитимемо деяку тотожність, то всі інші вважатимемо доведеними.

Адже, треба довести

Почнемо з правої частини

ми отримали ліву частину. Тотожність доведено.

Будь-яка теорема алгебри множин виводиться з тотожностей 2а) і 2б),тобто методом алгебраїчних перетворень.

Приклад 3.7. Доведемо властивість 8а) , послідовно використовуючи властивості 4б), 5а), 3а), 5б), 4а).

.