Приклади розв’язування задач
Задача 1. Визначити силу, яка діє на заряд q2 = –1·10-6 Кл (мал. 74), якщо заряди q1 = 1 · 10-7 Кл і q3 = 2 · 10-7 Кл знаходяться в повітрі на відстані AB = BC = 10 см.
Дано: q1 = 1 · 10-7 Кл; q2 = –1 · 10-6 Кл; q3 = 2 · 10-7 Кл; AB = BC = 10 см |
F - ? |
Н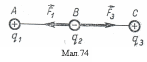
а
заряд q2
діють заряди q1
і q3
з силами, вектори яких
і
(див. мал.74 ). Сили
і
– сили притягання заряду q2
до зарядів q1
і q3,
вони направлені по одній прямій AC,
але протилежно напрямлені. Їх рівнодійна
направлена в сторону більшої сили
і за модулем дорівнює різниці їх модулів.
За законом Кулона знайдемо модулі сил
і
:
і
.
Відстань AB = BC = 0,1 м. Підставляючи числові значення, одержуємо ≈ 0,1 Н, ≈ 0,2 Н, а модуль F = 0,1 Н.
Відповідь: 0,1 Н.
Задача 2. Заряди q1 = q2 = q3 = 1·10-6 Кл розміщенні у вершинах рівностороннього трикутника із сторонами a = 20 см. Визначити силу, яка діє на один із цих зарядів з боку двох інших у повітрі.
Дано: q1 = q2 = q3 = 1 · 10-6 Кл; a = 20 см=0,2 м |
F - ? |
З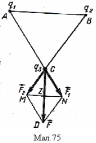
робимо
креслення (мал.75).
Визначимо силу, що діє на заряд q3,
який знаходиться в точці С.
Заряди q1
(в точці А)
і q2
(в точці В)
діють на заряд q3
з відповідними силами
і
.
Рівнодійну цих сил (
)
знайдемо за правилом паралелограма.
Для розв’язання
задачі будемо використовувати не
вектори, а їх модулі, які дорівнюють
довжинам відрізків, які на кресленні
відповідають векторам
,
,
.
Легко довести, що
=
,
,
оскільки
MCN
=
ACB
= 600. Тоді
,
в ∆ СNZ сторона
.
За законом Кулона модуль сили
;
=
0,02 Н;
F = 0,02 Н
·
·
2 ≈ 0,034 H.
Відповідь: 0,034 Н.
Задача 3.
Два заряди по 1·10-8
Кл знаходяться у повітрі на відстані 8
м один від одного. Визначити напруженість
у точці, що знаходиться на відстані 5 м
від обох зарядів. Точка і заряди
знаходяться у одній площині .
Дано: qA = qB = 1 · 10-8 Кл; AB = 8 м; АD = 5 м |
ED - ? |
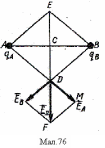
Як видно з мал.76, таких точок дві D і E. Тому розв’язання зробимо для однієї з них, наприклад для D.
EA
і EB
– модулі напруженостей
в точці D,
створені зарядами qA
і qB.
За умовою qA
= qB.
Загальна напруженість електричного
поля в точці D:
,
яку знаходимо як діагональ
паралелограма зі сторонами векторів
напруженості
і
.
Модулі напруженостей
,
а модуль напруженості ED знаходять із подібності ∆ AED і ∆ DMF:
,
або
.
З ∆ АСD
;
CD = 3 м,
тоді ЕD
= 6 м.
Отже
.
Підставляючи числові значення, отримаємо
ED
= 4,3 Н/Кл.
Напрямок сумарної напруженості показано на мал.76
Відповідь: 4,3 Н/Кл.
Задача 4.
На діелектричній нитці висить кулька
масою m.
Вся ця система знаходиться в однорідному
електростатичному полі, напруженість
якого
направлена вертикально вгору.
Визначити силу пружності нитки, коли
кулька не заряджена і коли їй надають
від’ємний заряд –
q.
Дано: m; E; – q |
Fпр - ? |
Коли кулька не заряджена, то
діє сила тяжіння
і сила пружності
.
Якщо кульку зарядити, то виникає ще й
електрична сила
(мал. 77), у результаті чого
сила пружності зміниться. Спроектуємо
ці сили на вісь Oy.
У першому випадку запишемо суму проекцій сил на вісь Oy і прирівняємо її до нуля:
,
тобто
.
У другому випадку сума проекцій сил буде іншою:
,
тобто
.
Відповідь:
,
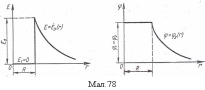
Задача 5. Суцільна металева сфера радіусом R = 20 см має рівномірно розподілений заряд поверхневої густини σ =10-9 Кл/м2. Визначити напруженість та потенціал електричного поля у точках на відстанях r1=16 см від центра сфери; на поверхні сфери та на відстані r2=36 см від центра сфери. Побудувати графіки залежності Е=Е(r) та φ=φ(r).
Дано: R = 0,2 м; σ = 10-9 Кл/м2; r1=0,16 м; r2=0,36 м |
Е1; Е2; Е3 -? φ1; φ2; φ3 -? |
Всередині сфери напруженість поля дорівнює нулю: Е1=0.
Потенціал всередині сфери дорівнює потенціалу на поверхні: φ1=φ2.
Заряджена сфера створює навколо себе поле, напруженість якого визначається за формулою точкового заряду.
Для відстані r
=R :
;
Е2=113
В/м.
;
φ2=22,6
В.
Для відстані r
= r2:
; Е3=34,5
В/м.
;
φ3=12,42
В.
Графіки показано на малюнку 78.
Відповідь: 0 В; 113 В/м; 34,5 В/м; φ1=φ2=22,6 В; 12,42 В.
З
адача
6. Електричне поле
створене зарядом 5·10-7
Кл, який знаходиться у середовищі з
діелектричною проникністю 2
(мал.79
). Визначити
різницю електричних потенціалів точок
В і
С, віддалених від заряду
на 5 см і 0,2 м. Яка робота виконується при
переміщенні електричного заряду 0,3·10-7
Кл між точками В
і С?
Дано: q = 5·10-7 Кл; q0 = 0,3·10-7 Кл; ε = 2; ε0 = 8,85·10-12 Кл2/(Н·м2); r1 = rB = 5·10-2 м; r2 = rC = 0,2 м |
U - ?, A - ? |
Використовуючи формулу φ = q/(4πε0εr), визначимо різницю електричних потенціалів точок В і С електричного поля:
U = φB
– φC =
=
.
Роботу по переміщенню заряду в електричному полі визначимо за формулою A = q0U.
Підставляючи числові значення матимемо:
,
А ≈ 0,3·10-7 Кл · 34·103 В ≈ 10-3 Дж = 1 мДж.
Відповідь: 34кВ; 1мДж.
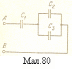Задача 7.
Три конденсатори з ємностями C1
= 0,2 мкФ, С2
= С3
= 0,4 мкФ з’єднані між собою як показано
на малюнку 80,
і приєднані до джерела
постійного струму UAB
= 250 В. Визначити загальний електричний
заряд, заряд і різницю потенціалів на
кожному з конденсаторів та електричну
енергію накопичену всією батареєю
конденсаторів.
Дано: C1 = 0,2 мкФ; С2 = С3 = 0,4 мкФ; UAB = 250 В |
q - ?, q1 - ?, q2 - ?, q3 - ?, U1 - ?, U2 - ?, U3 - ?, W - ? |
Загальний заряд визначимо за формулою q = CUAB,
де C
– ємність батареї конденсаторів, яку
визначимо з формули змішаного з’єднання:
.
Заряд першого конденсатора такий же, як і загальний заряд: q1 = q, а заряди на двох інших конденсаторах q2 = q3 = q/2.
Знаючи ємність і заряд кожного конденсатора, можемо визначити різницю потенціалів на їх обкладинках.
Для визначення енергії
накопиченої батареєю конденсаторів
використаємо формулу:
.
Заряд, накопичений батареєю,
Підставимо числові значення:
.
Заряди на окремих конденсаторах: q1 = 4·10-5 Кл, q2 = q3 = 2·10-5 Кл.
Визначимо різницю потенціалів на окремих конденсаторах і їхню загальну енергію:
;
.
.
Відповідь: q1 = 4∙10-5 Кл, q2 = q3 = 2·10-5 Кл; U1=200 В, U2=U3=50 В, W=5∙10-3 Дж.
Задача 8. Батарея із двох конденсаторів, з’єднаних послідовно і ємності яких 2 і 3 мкФ, заряджена до напруги 400 В. Визначити електроємність батареї і напругу на затискачах кожного конденсатора.
Дано: С1 = 2 мкФ; С2 = 3 мкФ; U = 400 В |
СБ - ? U1 - ? U2 - ? |
Загальну електроємність
батареї Сз
знаходимо за формулою
,
звідки
=
1,2 мкФ.
З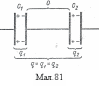
агальний
заряд батареї
q = СБU ; q=1,2·10-6 Ф · 400 В = 4,8·10-4 Кл.
При послідовному з’єднанні конденсаторів заряд на кожному з них дорівнює загальному заряду батареї: q = q1 = q2 (мал.81).
Напруга на конденсаторах:
=
240 В;
=
160 В.
Відповідь: СБ=1,2 мкФ; U1=240 В; U2=160 В.