Выпуклость, вогнутость, точки перегиба графика функции.
Находим вторую
производную
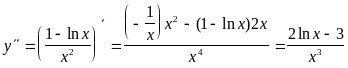 .
.
В
области допустимых значений вторая
производная точек разрыва не имеет. Для
определения точек, в которых она равна
нулю, решаем уравнение
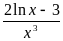 =0;
=0;
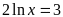 ;
;
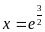 ;
;
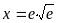 .
.
Определяем интервалы
знакопостоянства второй производной
и интервалы выпуклости и вогнутости
функции. Результаты сводим в таблицу.
x
|
(0;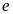
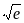 )
)
|
(
;+)
|
y
|
|
+
|
y
|
|
|
Вторая
производная меняет знак в точке х=
,следовательно, эта точка является
точкой перегиба. Вычислим значение
функции в этой точке. Имеем
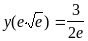 .
.
На основании
проведенного исследования строим график
функции.
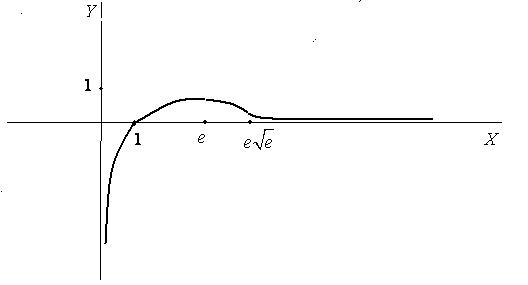
Таким образом мы
изучили с вами основные моменты
исследования функций и построения их
графиков. Некоторые особенности имеются
при исследовании периодических функций.
Их мы изучим на практическом занятии.


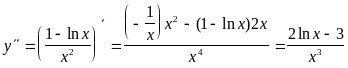 .
.