Лабораторная работа № 7

”Обработка экспериментальных данных”

Цель работы: Изучение средств MathCAD для решения задач обработки экспериментальных данных.

Задание к работе.

(A)Построить интерполяционный кубический сплайн для функции y=f(x),

заданной таблицей. Используя найденную зависимость, найти значение у в точке x = N + 0.55 , где N – номер варианта.

(B)Найти методом наименьших квадратов значения коэффициентов зависимости y = f (x) по заданным экспериментальным данным (табл. 1). Используя зависимость, найдите значение у в точке x = N + 0.55 , где N – но-

мер варианта, абсолютную погрешность в них и среднеквадратическую погрешность, построить графики.

(C)Постройте график z = f (x, y) двумерной сплайн-интерполяции по задан-

ным эмпирическим данным (массивы X, Y даны в табл.). Используя найден-

ную зависимость, найдите значение z в точке , где N

– номер варианта.

1. Начальные условия

Даны два массива X и Y. Они транспонированы

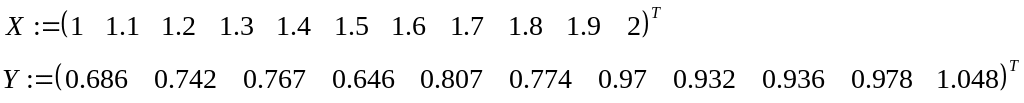
Сначала вводим параметр N,i ,x

Построим интерполяционный кубический сплайн, Таким образом, сплайн-аппроксимация проводится в два этапа. На первом с помощью функций cspline отыскивается вектор вторых производных при приближении в опорных точках к кубическому полиному, заданной векторами VX и VY ее значений (абсцисс и ординат). Затем, на втором этапе для каждой искомой точки вычисляется значение y(x) c помощью функции interp.

Находим значение при x=1+0.55=1.55

(B) Найти методом наименьших квадратов значения коэффициентов зависимостиy y=f(x) по заданным экспериментальным данным (табл. 1). Используя зависимость, найдите значение у в точке x = N + 0.55 , где N – номер варианта, абсолютную погрешность в них и среднеквадратическую погрешность, построить графики

Начальные условия даны два массива X и Y.

Решить эту задачу можно 2 способами. 1 метод с помощью встроенной функции line.

Запишем линейное уравнение виде y(x)=a*x+b

2 метод с помощью встроенных функций intercept и slope.

Сначала находим угловой коэффициент с помощью функции slope

Потом находим b, где пересекается с осью y. Воспользуемся функцией intercept

Запишем линейном виде.

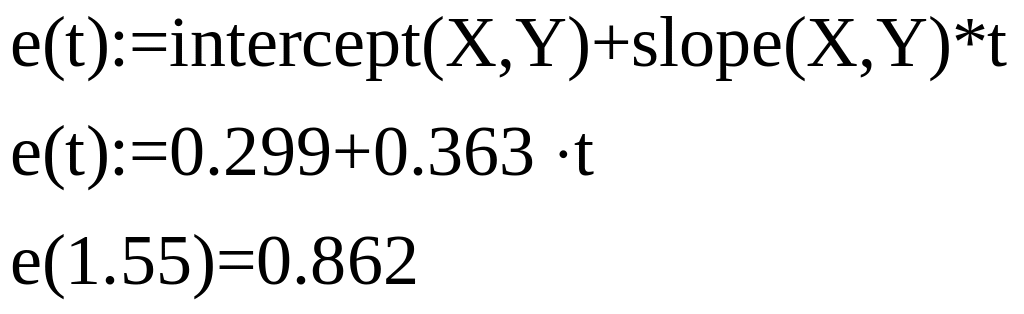
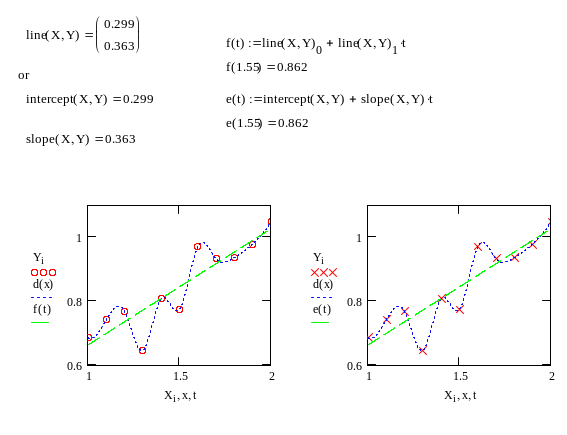
Лабораторная работа № 8

Цель работы: Получение навыков решения дифференциальных уравне-

ний с использованием встроенных функций MathCAD.

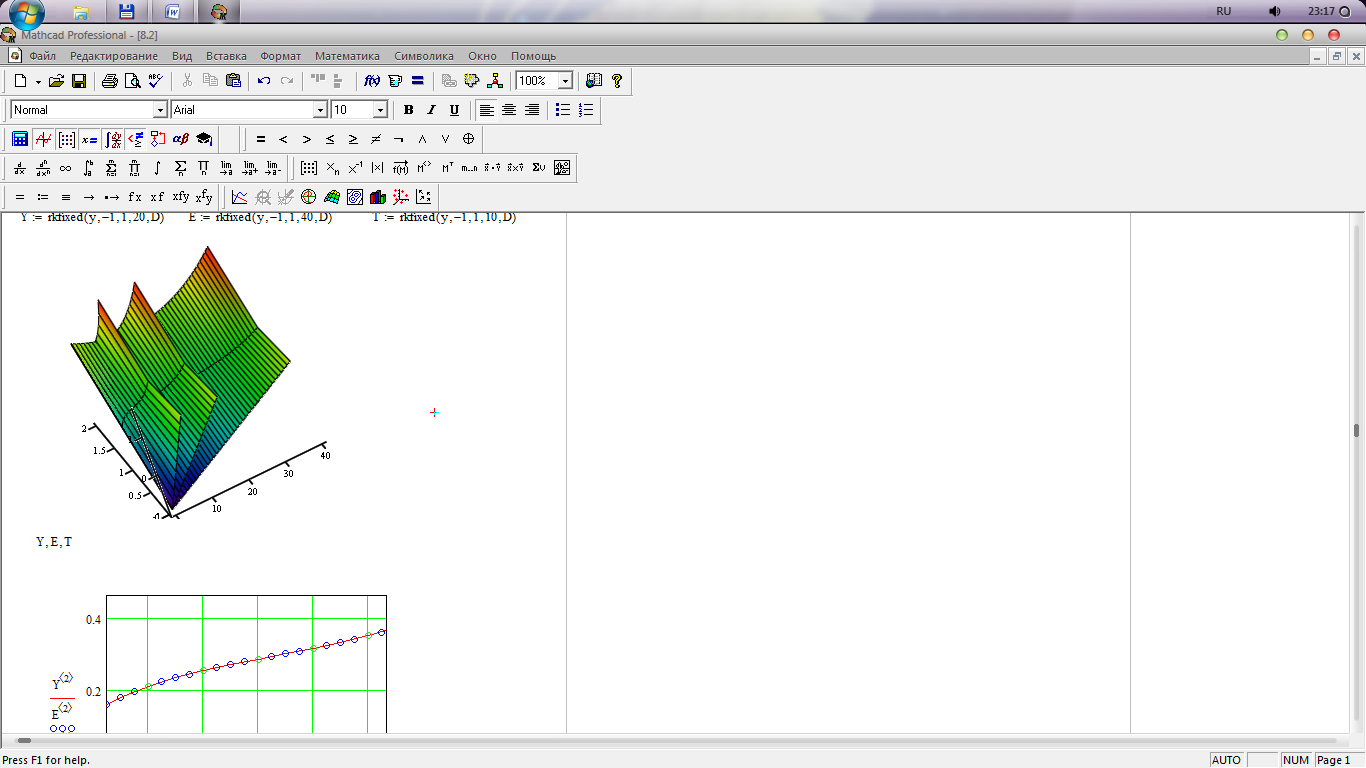
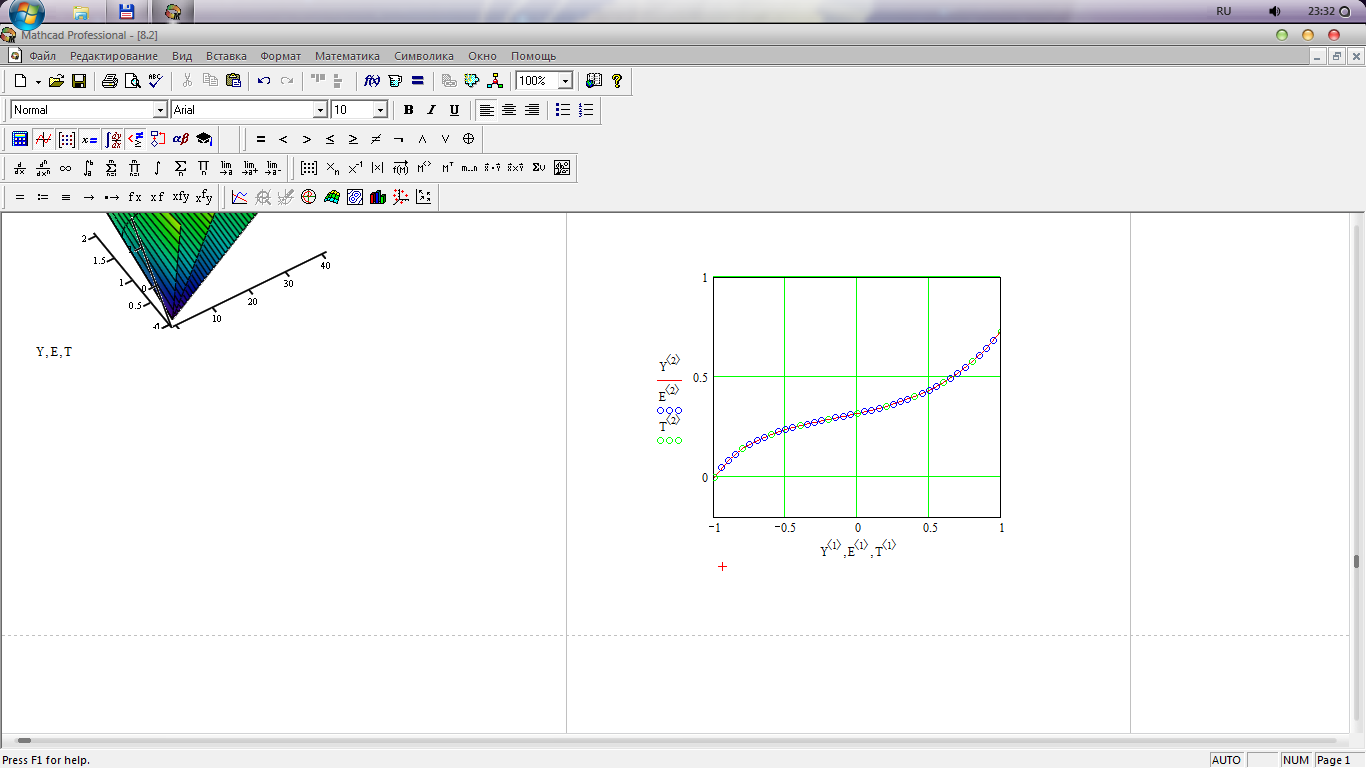
1. Задание к работе: Решите на отрезке [x₀,x_N] задачу Коши y′ = f(x,y), y(x₀)=y₀ методом Рунге-Кутты с постоянным шагом. Изобразите графики решений, вычисленных с шагами h, 2h и h/2. Значение x_N > x₀ выберите самостоятельно.

F(x,y,y’)=0

(e^x+1)dy+e^xdx=0 y(0)=0.5

3 шага.

Решаем первую часть задачи. Задаем D(x,y) и подставляя значения

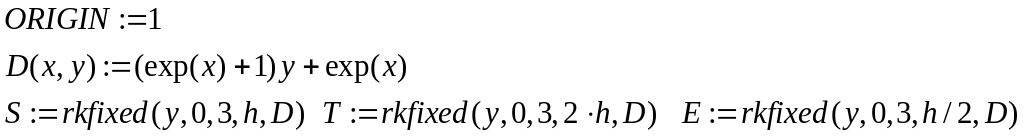
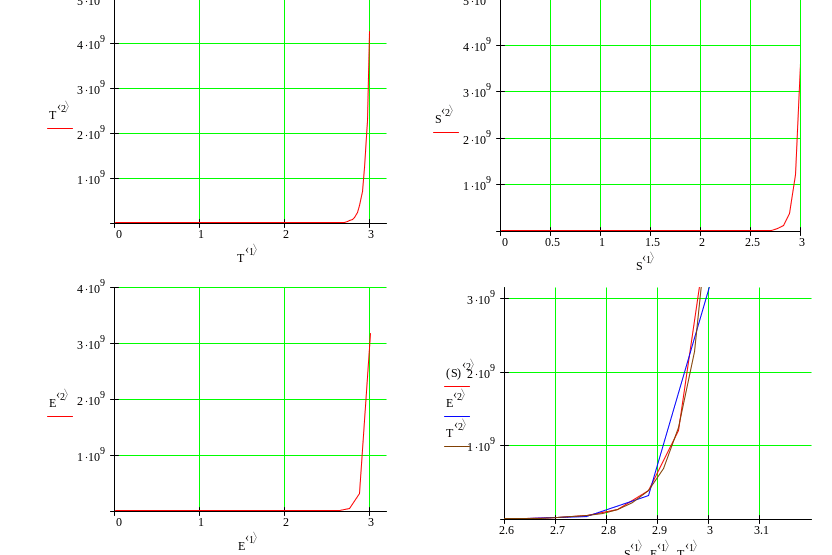
Найденные решения методом Рунге-Кутты с постоянным шагом.

2. Решить задачу Коши y1′ = f1(x, y1, y2 ) , y′2 = f2 (x, y1, y2 ) , y1(a)= y1,0 , y2(a) = y2,0 на отрезке [a,b] методом Рунге-Кутта с постоянным шагом h=0.1. Изобразите графики решений, вычисленных с шагами h, 2h и h/2.

Начальные условия.

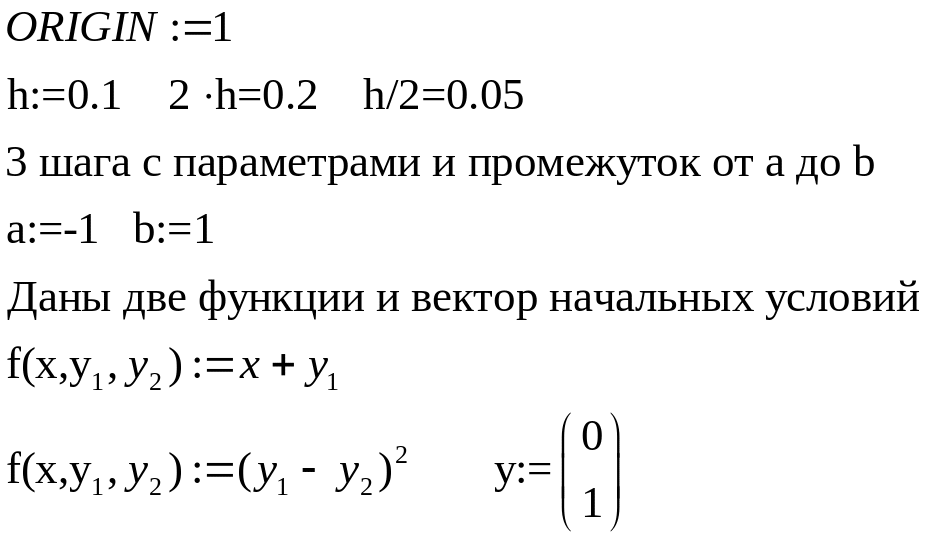
Заполняем систему дифференциальных уравнений и находим решение задачи коши несколькими шагами на h,2*h и h/2