Лабораторная работа 4. Оптимизация производственных функций

Оптимизация экономической статики

Здесь рассмотрены статистические модели, связанные с принятием решения в задаче потребительского выбора и оптимизации производственной функций.

Первая группа задач связана с понятием функции полезности, которая отражает предпочтения потребителя.

Естественно, у разных потребителей и предпочтения могут быть разными. Функция полезности является попыткой формализовать эту неформальную задачу. Вид этой функции и ее параметры (коэффициенты важности) характеризуют предпочтения конкретного потребителя.

Построить адекватную модель производства на основе законов физики, химии, балансовых и подобных законов пока еще, как правило, невыполнимая задача. В этих условиях часто прибегают к эмпирическому построению модели производства. Для этого собирают статистику о функционировании производства за определенный период и пытаются подобрать производственную функцию, задавая ее подходящий вид и определяя значения ее параметров из условия наилучшего соответствия экспериментальным данным.

С точки зрения методов оптимизации рассматриваемые задачи относятся к задачам нелинейного программирования с ограничениями, как правило, в виде неравенств.

Производственная функция (ПФ) , - это неотрицательная функция, определяющая значения объемов выпускаемой продукции (дохода) в зависимости от объема затрачиваемых ресурсов x. На микроэкономическом уровне ПФ определяет зависимость между объемом выпускаемой продукции и затратами фирмы (предприятия), на макроэкономическом уровне - подробную зависимость в масштабах региона или страны. Часто используют производственную функцию Кобба – Дугласа:

(13)

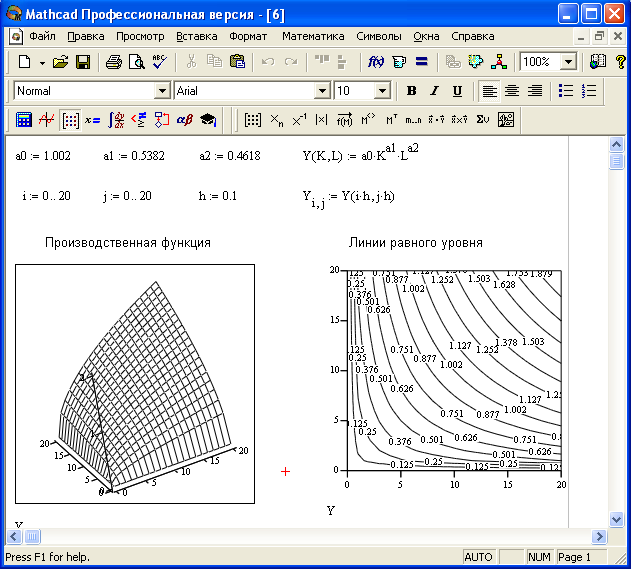
Рисунок 14. Графики производственной функции

Здесь K-затраты на капитал, L- затраты на труд. Параметры и график функции приведены в документе MathCAD (рис.14), где по оси х отложены объемы использования ресурса x ,по оси y - объемы использования ресурса x , по оси z-объемы производства f(x ,x ).

Формальные свойства ПФ:

1. – без затрат хотя бы одного ресурса нет выпуска.

2. - при увеличении затрат любого ресурса выпуск растет.

3. - убывающая эффективность затрат.

4. – эффективность каждой переменной не уменьшается с ростом любой переменной .

Очевидно, что значения ПФ расположены в положительной части пространства x, функция выпукла вверх и монотонно увеличивается с ростом аргументов.

Для учета научно-технического прогресса в функцию часто вводят дополнительный экспоненциальный множитель:

(14)

Для экономики бывшего СССР =0,0294.

Максимизация функции полезности без ограничений не имеет решения: функция неограниченно возрастает. Если ввести цену единицы капитализации и цену единицы труда , бюджетное ограничение , то тогда задача приобретает содержательный смысл:

(16)

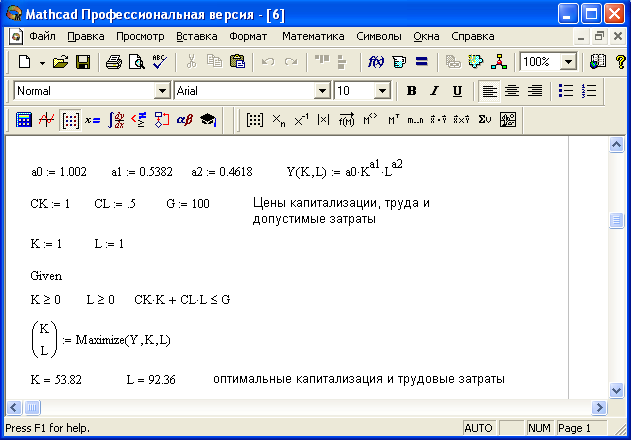
В документе MathCAD (рис.15) представлены результаты решения этой задачи для приведенной ПФ.

Рисунок 15. Оптимизация производственной функции

Аналогичная задача может быть представлена для предприятия несколько по-другому. Пусть произведенная продукция, определяемая производственной функцией f(x ,x ), имеет цену с₀, а затачиваемые ресурсы – цену с и с соответственно. Тогда нужно максимизировать прибыль – разницу между доходами и затратами :

(17)

при условии

(18)

Решение этой задачи при той же производственной функции дано в документе MathCAD на рис.16.

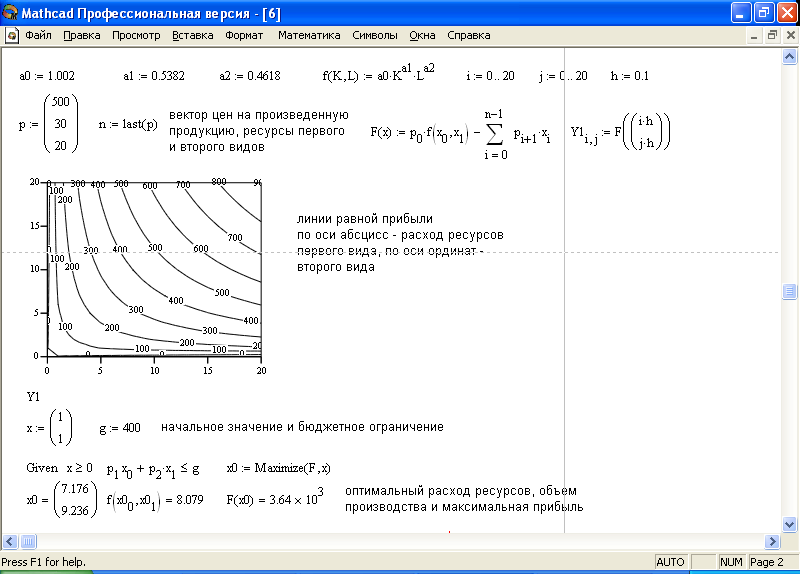
Рис. 16 – Оптимизация прибыли с использованием производственных функций

Более содержательной представляется задача распределения указанных ресурсов между несколькими предприятиями в задаче микроэкономики или несколькими отраслями в задаче макроэкономики со своими производственными функциями:

(19)

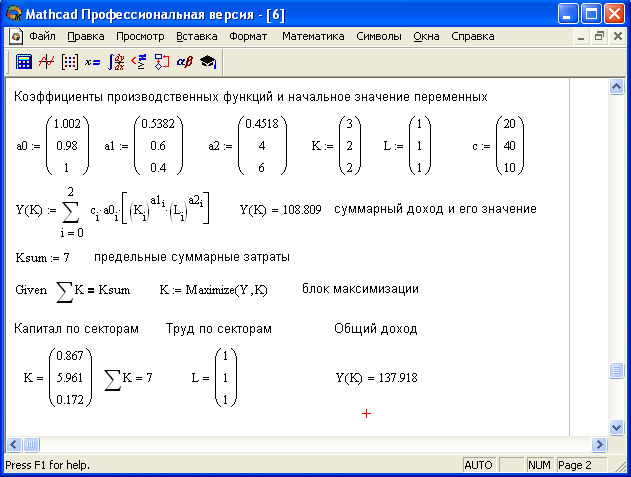
Рисунок 17. Оптимизация в трёхсекторной экономике

причем по каждому виду ресурса имеется ограничение

. (20)

Требуется максимизировать суммарный доход при указанных ограничениях. Решение этой задачи приведено на рисунке 17. В документе MathCAD для трех секторов экономики со своими производственными функциями и оптимальными вложениями капитала в эти секторы.